Арифметические действия являются основой математики и включают в себя операции сложения, вычитания, умножения и деления чисел. Одним из видов чисел, с которыми мы работаем, являются рациональные числа. В этой статье мы рассмотрим, что такое арифметические действия с рациональными числами и как их выполнять.
Рациональные числа представляют собой числа, которые могут быть представлены в виде дробей, где числитель и знаменатель являются целыми числами. Они включают в себя обыкновенные дроби, десятичные дроби и целые числа.
Чтобы выполнить арифметические действия с рациональными числами, мы используем те же операции, что и при работе с целыми числами. Например, сложение рациональных чисел выполняется путем сложения числителей и сохранения знаменателя неизменным, если знаменатели совпадают. Если знаменатели различаются, мы должны привести дроби к общему знаменателю, чтобы выполнить сложение.
Определение арифметических действий
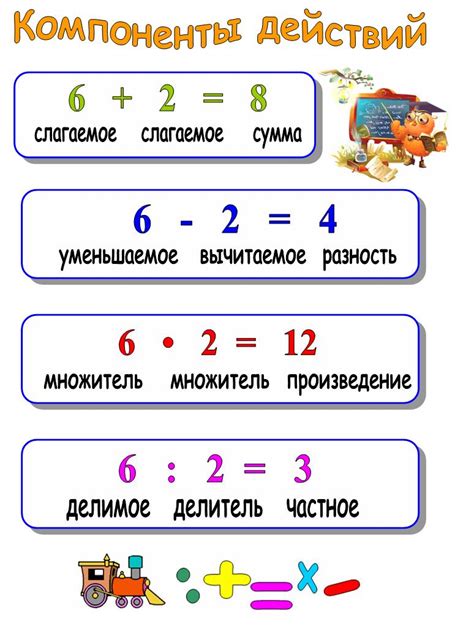
Сложение является базовым арифметическим действием и позволяет объединять два или более числа для получения их суммы. Обозначается знаком "+". Например, сложение чисел 3 и 4 будет выглядеть следующим образом: 3 + 4 = 7.
Вычитание выполняется для нахождения разности между двумя числами. Обозначается знаком "-". Например, разность чисел 7 и 3 будет выглядеть следующим образом: 7 - 3 = 4.
Умножение позволяет находить произведение двух или более чисел. Обозначается знаком "×" или "*". Например, умножение чисел 2 и 5 будет выглядеть следующим образом: 2 × 5 = 10.
Деление выполняется для нахождения отношения между двумя числами. Обозначается знаком "÷" или "/". Например, деление чисел 10 и 2 будет выглядеть следующим образом: 10 ÷ 2 = 5.
Выполняя арифметические действия, мы можем получать новые числовые значения, которые могут быть как рациональными, так и иррациональными. Умение правильно применять арифметические действия к числам является важным навыком и используется в различных сферах человеческой деятельности, включая финансы, науку и повседневные расчеты.
Арифметические действия: основные понятия и принципы

Основные понятия и принципы арифметических действий:
| Действие | Описание |
|---|---|
| Сложение | Сложение двух чисел даёт их сумму. При сложении рациональных чисел необходимо складывать числитель и знаменатель отдельно. |
| Вычитание | Вычитание одного числа из другого даёт их разность. При вычитании рациональных чисел необходимо вычитать числитель и знаменатель отдельно. |
| Умножение | Умножение двух чисел даёт их произведение. При умножении рациональных чисел необходимо умножать числитель и знаменатель отдельно. |
| Деление | Деление одного числа на другое даёт их частное. При делении рациональных чисел необходимо умножить делимое на обратную дробь делителя. |
Арифметические действия с рациональными числами включают в себя также правила приоритета операций и дистрибутивности. Приоритет сложения и вычитания выше, чем умножения и деления. Дистрибутивность означает, что умножение или деление двух чисел, совершаемые с третьим числом, можно выполнить отдельно для каждого из них, а затем сложить или вычесть полученные результаты.
Сложение и вычитание рациональных чисел: правила и примеры

Арифметические действия с рациональными числами включают в себя сложение и вычитание. Сложение и вычитание рациональных чисел можно выполнять как с положительными, так и с отрицательными числами.
Правила сложения и вычитания рациональных чисел:
| Знаки чисел | Правило | Пример |
|---|---|---|
| Оба числа положительные | Просто сложите два числа | 2 + 3 = 5 |
| Оба числа отрицательные | Удалите знак минус и сложите два числа, затем поставьте знак минус перед результатом | -4 + (-7) = -(4 + 7) = -11 |
| Числа разных знаков | Найдите разностные значения чисел по абсолютному значению и используйте знак числа с большим абсолютным значением | 6 + (-9) = 6 - 9 = -3 |
Примеры сложения и вычитания рациональных чисел:
- 3 + 7 = 10
- -5 + 2 = -3
- 4 - (-9) = 4 + 9 = 13
- -8 - (-3) = -8 + 3 = -5
- 5 + (-10) = 5 - 10 = -5
При выполнении сложения и вычитания рациональных чисел важно учитывать правила и следовать им. Таким образом, можно уверенно выполнять эти арифметические операции и получать правильный результат.
Умножение и деление рациональных чисел: методы и примеры

Если у нас есть два рациональных числа, например, 2/3 и 5/6, то мы можем их перемножить следующим образом:
2/3 * 5/6 = (2 * 5) / (3 * 6) = 10/18
Для упрощения дроби следует использовать НОД (наибольший общий делитель) числителя и знаменателя. В данном примере, НОД числителя 10 и знаменателя 18 равен 2, поэтому мы можем упростить дробь:
10/18 = 5/9
Деление рациональных чисел – это операция, обратная умножению. Чтобы разделить одно рациональное число на другое, нужно умножить первое число на обратное второму. Обратное число для рационального числа a/b можно найти путем поменяв числитель и знаменатель местами: b/a.
Рассмотрим пример деления рациональных чисел 3/4 и 2/5:
(3/4) / (2/5) = (3/4) * (5/2) = (3 * 5) / (4 * 2) = 15/8
Как и при умножении, мы можем упростить дробь с помощью НОД числителя 15 и знаменателя 8:
15/8 – это упрощенная дробь, полученная в результате деления рациональных чисел 3/4 и 2/5.



