Алгебраическое выражение – одно из основных понятий, которое изучается в 7 классе в рамках курса алгебры. Данное понятие становится ключевым при изучении алгебры и выполняет важную роль в решении математических задач. Поэтому, чтобы успешно освоить этот предмет, необходимо понимать, что такое алгебраическое выражение и как его использовать.
Алгебраическое выражение – это математическое выражение, которое состоит из чисел, букв и знаков операций (сложение, вычитание, умножение и деление). В алгебраическом выражении буквы играют роль переменных, то есть их значения могут меняться в зависимости от контекста задачи. Такие выражения позволяют описать различные зависимости между переменными и решать задачи, связанные с этими зависимостями.
Например, выражение 2x + 3 описывает зависимость между переменной x и числами 2 и 3. Здесь буква x выполняет роль переменной, значение которой неизвестно. Алгебраические выражения позволяют вычислять значения функций, находить корни уравнений, выражать зависимости в физике и других науках.
Алгебраическое выражение в 7 классе: понятие и особенности

Основные особенности алгебраических выражений в 7 классе:
- Переменные: в алгебраическом выражении могут присутствовать переменные, которые обозначают неизвестные значения. Обычно используются буквы для обозначения переменных, например, x, y, z.
- Числа: выражение может содержать числа, как конкретные значения, так и алгебраические выражения.
- Математические операции: выражение может включать математические операции, такие как сложение, вычитание, умножение и деление. Также могут использоваться степень и корень.
- Коэффициенты: в алгебраическом выражении коэффициенты могут умножаться на переменные. Они могут быть как целыми числами, так и дробями.
- Степени: в выражении могут присутствовать степени переменных. Они обычно записываются в виде возведения в степень, например, x^2.
- Комбинированные операции: в одном выражении могут использоваться несколько различных математических операций, например, сложение и умножение.
Знание и понимание алгебраических выражений позволяет ученикам решать уравнения и неравенства, а также проводить различные операции с алгебраическими выражениями. Они становятся основой для более сложного математического анализа и расширения знаний в будущих классах.
Определение алгебраического выражения
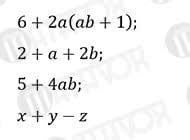
В алгебраическом выражении переменные представляют неизвестные значения, которые могут быть заменены на конкретные числа. Коэффициенты, запи-санные перед переменными, определяют их вклад в выражение. Например, в выражении 3x + 2y - 5z, переменные x, y и z имеют коэффициенты 3, 2 и -5 соответственно.
Алгебраические выражения могут быть использованы для описания и решения различных математических и реальных задач. Они позволяют представлять зависимости между величинами и проводить анализ различных математических моделей. Кроме того, они являются основой для изучения алгебры и других разделов математики.
Примеры алгебраических выражений:
- 3x + 2y - 5z
- 2a^2 - b + 4c
- 5(x + 3y) - 2z
- 2m^2 + 3mn - 7n^2
Структура алгебраического выражения
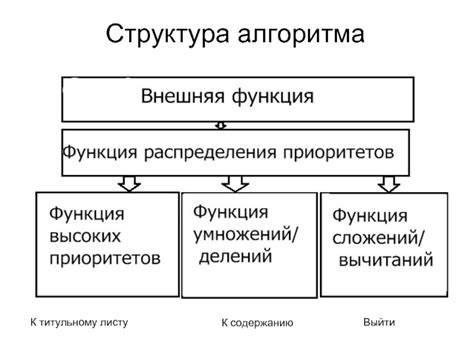
Структура алгебраического выражения может быть представлена следующим образом:
- Переменные - это буквенные символы, которые представляют неизвестные значения или значения, которые могут меняться. Например, x или y.
- Числа - это константы, которые имеют определенное значение. Например, 2 или 5. Числа могут быть как натуральными, так и рациональными.
- Арифметические операции - это действия, которые можно выполнить над переменными и числами для получения новых значений. Операции могут включать сложение, вычитание, умножение и деление.
Структура алгебраического выражения определяет порядок выполнения операций при вычислении значения выражения. Существуют математические правила и конвенции, которые определяют, какие операции выполнять в первую очередь.
Например, при вычислении выражения 2 + 3 * 4, сначала выполняется умножение, затем сложение, в соответствии с правилом приоритета операций.
Структура алгебраического выражения играет важную роль в алгебре, так как позволяет более точно определить значение выражения и использовать его в решении различных математических задач.
Основные операции с алгебраическими выражениями

Алгебраические выражения играют важную роль в математике и используются для описания различных математических операций. Существуют несколько основных операций, которые можно выполнять с алгебраическими выражениями.
1. Сложение алгебраических выражений: для выполнения операции сложения следует объединить все подобные члены. Подобные члены имеют одинаковые переменные с одинаковыми степенями. Например, выражения 3x + 4y + 2x + 5y можно сложить, объединив подобные члены: (3x + 2x) + (4y + 5y) = 5x + 9y.
2. Вычитание алгебраических выражений: для выполнения операции вычитания следует изменить знаки второго выражения и затем сложить их, как при сложении. Например, для выполнения операции 3x - (2x + 4y) можно сначала изменить знаки в скобках, получив -2x - 4y, и затем сложить два выражения: 3x + (-2x - 4y) = 3x - 2x - 4y = x - 4y.
3. Умножение алгебраических выражений: для выполнения операции умножения следует перемножить все члены первого выражения на каждый член второго выражения. Например, для выполнения операции (2x + 3y) * (4x - 5y) можно раскрыть скобки и перемножить каждый член первого выражения на каждый член второго выражения: 2x * 4x + 2x * (-5y) + 3y * 4x + 3y * (-5y) = 8x^2 - 10xy + 12xy - 15y^2 = 8x^2 + 2xy - 15y^2.
4. Деление алгебраических выражений: для выполнения операции деления следует разделить каждый член первого выражения на каждый член второго выражения. Деление алгебраических выражений обычно сводится к умножению и обратному применению операции умножения. Например, для деления (6x^2 + 9xy) на (3x) можно сократить по общим множителям и получить: (6x^2 + 9xy) / (3x) = 2x + 3y.
Операции с алгебраическими выражениями могут быть сложными, поэтому важно понимать правила каждой операции и применять их правильно. Правильное выполнение операций позволяет упростить выражения и решать различные математические задачи.
Примеры алгебраических выражений в 7 классе

Вот несколько примеров алгебраических выражений в 7 классе:
- 3x - это выражение, в котором умножают число 3 на переменную x. Здесь 3 называется коэффициентом, а x - переменной. Мы можем изменять значение переменной x и получать различные результаты.
- 5x + 2y - это выражение, в котором умножают число 5 на переменную x и число 2 на переменную y, а затем складывают результаты. Здесь x и y являются переменными, а 5 и 2 - коэффициентами.
- 2a - 3b + 7c - это выражение, в котором умножают число 2 на переменную a, число -3 на переменную b и число 7 на переменную c, а затем складывают результаты. Здесь a, b и c - переменные, а 2, -3 и 7 - коэффициенты.
Это только некоторые примеры алгебраических выражений, которые мы изучаем в 7 классе. При решении задач и упражнений вам будут предложены различные выражения, которые вы должны уметь анализировать и вычислять. Постепенно вы научитесь работать с более сложными и интересными алгебраическими выражениями. Удачи в изучении алгебры!



