Алгебраическая дробь – это особый вид выражений, в котором числители и знаменатели являются алгебраическими выражениями. Алгебраические дроби играют важную роль в математике и широко используются в алгебре и анализе. Они позволяют работать с неизвестными переменными и решать сложные уравнения и неравенства.
Восьмой класс – это ключевая ступень обучения алгебре. На этом уровне ученики изучают основные понятия и правила работы с алгебраическими дробями. Для лучшего усвоения материала рекомендуется использовать видеоуроки.
Видеоуроки – это удобный способ изучения материала, особенно в случае сложных и абстрактных концепций, таких как алгебраические дроби. Они позволяют ученикам видеть, каким образом применяются правила и методы решения задач. Кроме того, видеоуроки позволяют повторять материал неограниченное число раз, что укрепляет понимание и запоминание.
Алгебраическая дробь в 8 классе: основы

Основные понятия:
1. Числитель и знаменатель: Числитель – это выражение, стоящее вверху дроби; знаменатель – это выражение, стоящее внизу дроби. Например, в алгебраической дроби 3x/(2x+1) числитель равен 3x, а знаменатель равен 2x+1.
2. Определенность алгебраической дроби: Алгебраическая дробь называется определенной, если знаменатель не равен нулю. Если знаменатель равен нулю, то алгебраическая дробь называется неопределенной. Например, дробь 1/(x-2) будет неопределенной, если x-2=0 уравнение не имеет решений.
Основные правила:
1. Сложение и вычитание дробей: Дроби можно складывать и вычитать, если они имеют общий знаменатель. Для этого нужно сложить (вычесть) числители и записать результат над общим знаменателем. Например, для дробей 1/2 и 3/4 с общим знаменателем 4, получим (1+3)/4=4/4=1.
2. Умножение и деление дробей: Для умножения дробей нужно умножить числители и знаменатели. Например, дроби 2/3 и 4/5 можно умножить: (2*4)/(3*5)=8/15. Для деления дробей нужно умножить делимую дробь на обратную второй дроби. Например, 2/3 поделить на 4/5 будет: (2/3) * (5/4) = 10/12 = 5/6.
Важно помнить о правилах упрощения и сокращения дробей. Для этого нужно найти общие делители числителя и знаменателя и поделить их на них.
Что такое алгебраическая дробь?

(Anxn + An-1xn-1 + ... + A1x + A0) / (Bmxm + Bm-1xm-1 + ... + B1x + B0)
где An, An-1, ..., A1, A0, Bm, Bm-1, ..., B1, B0 - коэффициенты, x - переменная, n - степень числителя, m - степень знаменателя.
Алгебраические дроби играют важную роль в алгебре и математическом анализе, так как они используются для работы с рациональными функциями. Рациональная функция представляет собой отношение двух многочленов, где многочлены могут быть сложными алгебраическими дробями.
Алгебраические дроби могут быть упрощены путем раскрытия скобок, сокращения общих множителей в числителе и знаменателе, а также приведения подобных слагаемых.
Алгебраическая дробь может иметь особые точки, называемые «корнями знаменателя». Корни знаменателя являются значениями переменной, которые делают знаменатель равным нулю. Они имеют особое значение при вычислении значения алгебраической дроби.
Понимание алгебраических дробей важно для работы с рациональными функциями, решения уравнений, графиков и множества других алгебраических задач.
Как упростить алгебраическую дробь?

Для упрощения алгебраической дроби сначала необходимо провести факторизацию числителя и знаменателя. Факторизация позволяет разложить числитель и знаменатель на простые множители и выделить общие множители, которые можно сократить.
Затем следует проверить, можно ли сократить общие множители в числителе и знаменателе. Если есть общие множители, то их можно сократить, оставив только неприводимую дробь.
Далее, если числитель и знаменатель можно раскрыть скобки, то это следует сделать. Раскрытие скобок позволяет упростить дробь и привести ее к более простому виду.
В конечном итоге, после проведения всех упрощений, необходимо записать алгебраическую дробь в наиболее упрощенном виде, сократив все общие множители и раскрыв скобки, если это возможно.
Упрощение алгебраической дроби является важным шагом в решении задач и упрощении математических выражений. Правильное упрощение позволяет проводить дальнейшие операции с дробью, такие как сложение, вычитание, умножение и деление.
Основные операции с алгебраическими дробями
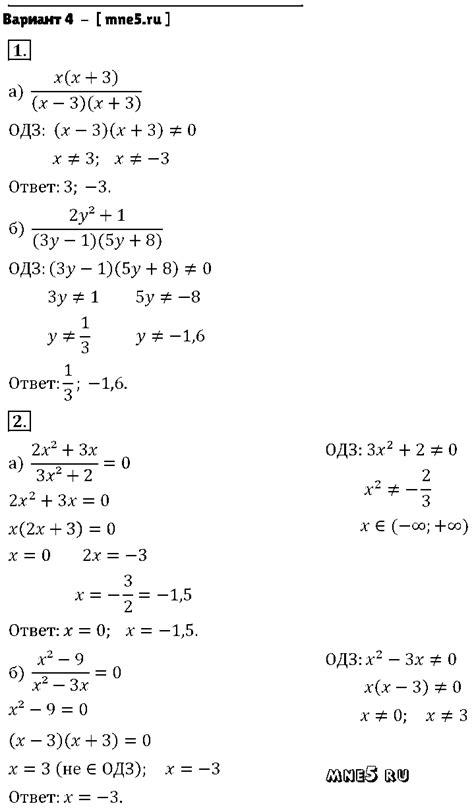
Алгебраическая дробь представляет собой выражение вида:
(p(x))/(q(x)), где p(x) и q(x) - многочлены с переменной x.
Основные операции с алгебраическими дробями включают:
- Сложение и вычитание алгебраических дробей.
- Умножение и деление алгебраических дробей.
- Сокращение алгебраических дробей.
Для сложения алгебраических дробей необходимо привести знаменатели к общему знаменателю и выполнять операцию с числителями. Результат сложения будет иметь тот же знаменатель, что и исходные дроби.
Умножение алгебраических дробей выполняется путем перемножения числителей и знаменателей. Затем, если возможно, выполняется сокращение полученной дроби.
Деление алгебраических дробей аналогично умножению, но с изменением знака у делителя.
Сокращение алгебраических дробей проводится путем выделения общих множителей в числителе и знаменателе и их сокращения.
Правила для выполнения этих операций основываются на законах арифметики и свойствах многочленов.
Как решать уравнения с алгебраическими дробями?

Решение уравнений с алгебраическими дробями может представлять некоторые сложности, но если следовать определенным шагам, задача может быть упрощена. Вот несколько шагов, которые могут помочь вам решить уравнения с алгебраическими дробями:
1. Упрощение алгебраических дробей:
Первым шагом в решении уравнений с алгебраическими дробями является упрощение дробей. Для этого вы можете разложить дроби на множители и применить соответствующие алгебраические операции для упрощения.
2. Нахождение общего знаменателя:
Для решения уравнений с алгебраическими дробями обычно требуется найти общий знаменатель для всех дробей. Чтобы найти общий знаменатель, вы можете использовать метод наименьших общих кратных (НОК).
3. Приведение к общему знаменателю:
После нахождения общего знаменателя, вам нужно привести все дроби к общему знаменателю путем домножения каждой дроби на соответствующий множитель.
4. Решение уравнения:
После приведения дробей к общему знаменателю, вы можете приступить к решению самого уравнения. Выполняйте необходимые алгебраические операции для получения значения неизвестной переменной.
5. Проверка решений:
В конце решения уравнения с алгебраическими дробями всегда необходимо провести проверку, подставив найденное значение переменной обратно в исходное уравнение. Если при подстановке оба выражения совпадают, то ваше решение верно.
С помощью этих шагов вы сможете решать уравнения с алгебраическими дробями и получать правильные ответы. Важно при выполнении каждого шага быть внимательным и не допускать ошибок, чтобы получить точное решение уравнения.
Методы сокращения и расширения алгебраических дробей

Метод сокращения алгебраической дроби заключается в выделении общего множителя в числителе и знаменателе дроби. Если общий множитель найден, его можно сократить и оставшуюся дробь записать в упрощенном виде. Например, если имеется дробь a/ab, где a и b - многочлены, то можно сократить дробь общим множителем a и получить результат 1/b.
Метод расширения алгебраической дроби применяется, если числитель и знаменатель дроби не имеют общих множителей, но требуется получить некоторую упрощенную форму дроби. В этом случае, можно домножить числитель и знаменатель на один и тот же многочлен (например, знаменатель), чтобы получить эквивалентную дробь с удобными свойствами. Например, если имеется дробь a/b, то при расширении дроби можно умножить числитель и знаменатель на многочлен b и получить результат ab/b^2 = a/b.
Однако, следует помнить, что во избежание ошибок при работе с алгебраическими дробями, после сокращения или расширения дроби, следует проверить полученное упрощенное выражение на его правильность.
Примеры решения задач с алгебраическими дробями

Алгебраические дроби широко используются для решения различного рода задач. Рассмотрим несколько примеров решения задач с использованием алгебраических дробей.
Пример 1:
Разложим рациональную функцию на простейшие дроби:
f(x) = (x^2 + 3x - 2) / (x^2 + 2x - 8)
Для начала найдем корни знаменателя и занесем их в таблицу:
| Корень | Кратность |
|---|---|
| x = 2 | 1 |
| x = -4 | 1 |
Далее выразим функцию f(x) в виде суммы простейших дробей:
f(x) = A/(x-2) + B/(x+4)
Умножим обе части уравнения на (x^2 + 2x - 8) и подставим значения в знаменатели:
(x^2 + 3x - 2) = A(x+4) + B(x-2)
Разложим полученное уравнение на два отдельных уравнения по степени x и приравняем коэффициенты нулю:
x^2: 1 = A + B
x: 3 = 4A - 2B
Систему уравнений решаем методом подстановки и находим значения A и B:
A = 1/3
B = 2/3
Итак, исходная функция f(x) разложена на простейшие дроби:
f(x) = 1/3(x-2) + 2/3(x+4)
Пример 2:
Решим уравнение с алгебраическими дробями:
(3/x) + (5/(x+1)) = 8/(x+2)
Для начала умножим обе части уравнения на (x * (x+1) * (x+2)), чтобы избавиться от знаменателей:
3 * (x+1) * (x+2) + 5 * x * (x+2) = 8 * x * (x+1)
Раскрываем скобки и упрощаем уравнение:
3x^2 + 9x + 6 + 5x^2 + 10x = 8x^2 + 8x
8x^2 + 10x + 6 = 8x^2 + 8x
Сократим коэффициенты перед x^2:
8x + 6 = 8x
6 = 0
Из полученного уравнения видим, что уравнение не имеет решения.
Это были два примера решения задач с алгебраическими дробями. Важно уметь правильно разлагать рациональные функции на простейшие дроби и решать уравнения, содержащие алгебраические дроби.
Видеоуроки по алгебраическим дробям в 8 классе
- Алгебраические дроби: введение и базовые принципы - этот урок представляет основные понятия и правила работы с алгебраическими дробями. Учащиеся узнают, как упрощать алгебраические дроби, как выполнять операции с дробями (сложение, вычитание, умножение, деление) и как находить общий знаменатель.
- Уравнения с алгебраическими дробями - в этом уроке объясняется, как решать уравнения, содержащие алгебраические дроби. Ученики узнают, как приводить уравнения к общему знаменателю, как упрощать дроби и как находить значение неизвестной переменной.
- Примеры и практические задания - в этом уроке предлагаются примеры и задания для практики работы с алгебраическими дробями. Учащиеся могут применить свои знания, решая разнообразные задачи и проверяя свои навыки.
Видеоуроки помогут учащимся лучше понять материал и освоить базовые принципы работы с алгебраическими дробями. Они могут быть использованы в качестве дополнительного материала для самостоятельного изучения или в качестве подготовки к урокам в классе.



