Уважаемые родители и ученики!
Мы рады сообщить вам о том, что начинается новый период обучения по предмету "Алгебра" для 7 класса. Этот увлекательный курс позволит ученикам развивать логическое и абстрактное мышление, обрести навыки решения математических задач и приобрести базовые знания алгебры.
В течение учебного года ученики изучат такие темы, как: арифметические действия с алгебраическими выражениями, раскрытие скобок, упрощение выражений, уравнения и неравенства, системы уравнений, пропорциональность, дроби, проценты и другие основные понятия алгебры. Ученикам будет предложено много задач и примеров для тренировки.
Мы стремимся сделать процесс обучения интересным и доступным для каждого ученика. Наши опытные учителя подготовили увлекательные уроки и интерактивные задания, чтобы помочь ученикам углубить свои знания и навыки в алгебре. Мы уверены, что благодаря этому курсу, ученики разовьют в себе уверенность в своих знаниях и смогут успешно применить их в решении различных математических задач.
Основные понятия алгебры

Переменная – это символ или буква, которая может представлять любое число или значение. Она используется для обозначения неизвестного значения в выражениях и уравнениях. Например, в выражении "2x + 3" переменная "x" представляет неизвестное число.
Выражение – это математическая конструкция, составленная из переменных, чисел и операций. Оно может быть как числовым, так и алгебраическим. Примеры выражений включают "3x + 5", "2a - 7" и "4(x + 2)".
Уравнение – это математическое выражение, которое утверждает равенство двух выражений или значений. Оно содержит знак равенства "=" и может иметь одну или несколько переменных. Решение уравнения – это нахождение значения переменной, при котором оба выражения равны. Например, уравнение "2x + 3 = 7" имеет решение x = 2.
Система уравнений – это группа двух или более уравнений, которые рассматриваются вместе. Решение системы уравнений – это нахождение значений переменных, при которых все уравнения системы выполняются одновременно. Например, система уравнений "2x + y = 5" и "x - y = 1" имеет решение x = 2, y = 1.
Арифметические операции в алгебре

Сложение - это операция, которая объединяет два или больше числа в одно число, которое называется суммой. Например, 3 + 5 = 8. В алгебре, сложение также может выполняться с использованием переменных, например, a + b.
Вычитание - это операция, обратная сложению. Она позволяет вычитать одно число из другого. Например, 8 - 3 = 5. В алгебре, вычитание также может использоваться с переменными, например, a - b.
Умножение - это операция, которая объединяет два или больше числа, чтобы получить их произведение. Например, 4 * 2 = 8. В алгебре, умножение также может выполняться с использованием переменных, например, a * b.
Деление - это операция, обратная умножению. Она позволяет разделить одно число на другое. Например, 9 / 3 = 3. В алгебре, деление может быть применено к переменным, например, a / b.
Арифметические операции имеют свои правила и свойства, которые помогают упростить их выполнение. Важно учитывать эти правила при работе с алгебраическими выражениями и уравнениями.
- При сложении и умножении, порядок чисел не важен: a + b = b + a, a * b = b * a.
- При сложении и умножении, можно изменять порядок скобок: (a + b) + c = a + (b + c), (a * b) * c = a * (b * c).
- При умножении и делении, можно сокращать одинаковые члены: a * b + a * c = a * (b + c), a * b / a = b.
- При умножении или делении числа на себя, результат всегда равен 1: a / a = 1.
Изучение арифметических операций в алгебре помогает развить навыки аналитического мышления и абстрактного рассуждения, которые являются основой для более сложных математических концепций и проблем.
Основные свойства алгебры

| Свойство | Описание |
| Коммутативность сложения и умножения | Порядок слагаемых или множителей не влияет на результат |
| Ассоциативность сложения и умножения | Сумма или произведение не зависят от расстановки скобок |
| Нейтральность по сложению и умножению | Существуют нейтральные элементы, которые не изменяют другие элементы при сложении или умножении |
| Обратимость по сложению и умножению | Каждый элемент имеет обратный элемент относительно сложения или умножения |
| Дистрибутивность умножения относительно сложения | Умножение распределяется на сложение |
Эти свойства позволяют выполнять алгебраические операции, решать уравнения и сравнивать числа. Они также образуют основу для более сложных понятий и теорем в алгебре.
Решение уравнений в алгебре

Для решения уравнений мы используем различные методы, основанные на свойствах алгебраических операций. Одним из самых простых методов решения уравнений является применение операций сложения, вычитания, умножения и деления для того, чтобы выразить неизвестную в явном виде.
При работе с уравнениями мы также используем свойства равенства, такие как коммутативность, ассоциативность и дистрибутивность. С помощью этих свойств мы можем изменять порядок операций и объединять подобные слагаемые или множители.
Важной частью решения уравнений является проверка полученного решения. Для этого подставляем найденные значения неизвестных в исходное уравнение и проверяем, что оно становится истинным.
Решение уравнений в алгебре требует внимания, аккуратности и применения различных математических приемов. При практике решения уравнений вы будете развивать логическое мышление и навыки работы с алгебраическими выражениями.
Пример:
Решим уравнение: 2x + 5 = 13.
Чтобы избавиться от слагаемого 5, вычтем его из обеих частей уравнения:
2x + 5 - 5 = 13 - 5
2x = 8
Затем, чтобы избавиться от коэффициента 2, разделим обе части уравнения на 2:
2x/2 = 8/2
x = 4
Проверим наше решение, подставив x = 4 в исходное уравнение:
2*4 + 5 = 13
8 + 5 = 13
13 = 13
Уравнение верно, значит, наше решение x = 4 является корректным.
Формулы и выражения в алгебре
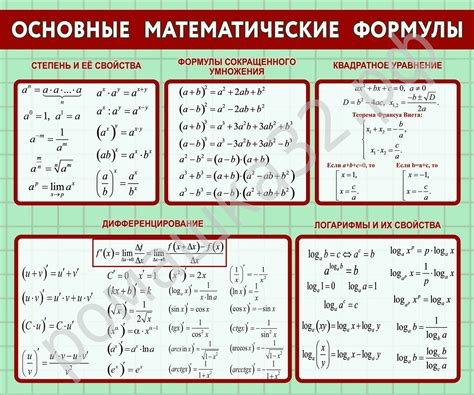
Мы используем различные символы и знаки для обозначения операций в алгебре. Например, знак "плюс" (+) обозначает сложение, знак "минус" (-) - вычитание, знак "знакоместитель" (*) - умножение, знак "делить" (/) - деление. Кроме того, мы также используем скобки для определения порядка операций.
Одной из основных формул в алгебре является формула для расчета площади прямоугольника: S = a * b, где S - площадь, a - длина стороны, b - ширина стороны. Для расчета периметра прямоугольника мы используем формулу: P = 2 * (a + b).
В алгебре мы также работаем с алгебраическими выражениями, которые содержат переменные и операции. Например, выражение 3a + 2b означает, что мы умножаем переменную a на 3, переменную b на 2 и складываем результаты. Алгебраические выражения можно упрощать, сокращая подобные слагаемые.
Формулы и выражения помогают нам решать множество задач в алгебре. Они позволяют нам проводить вычисления, находить неизвестные значения и решать уравнения. При изучении алгебры важно усвоить основные формулы и научиться правильно работать с выражениями.
Примеры задач по алгебре
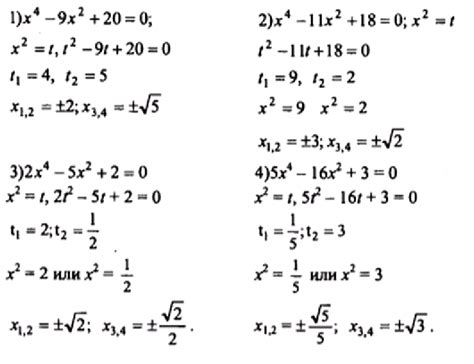
Ниже представлены несколько примеров задач по алгебре для учащихся 7 класса:
Пример 1:
Решите уравнение 3x + 7 = 22.
Решение:
Вычтем 7 с обеих сторон:
3x = 15
Разделим обе стороны на 3:
x = 5
Ответ: x = 5
Пример 2:
Вычислите значение выражения 2(3 + 5) - 4.
Решение:
Сначала выполним операцию в скобках:
3 + 5 = 8
Затем умножим полученное значение на 2:
2 * 8 = 16
Выполним вычитание 4:
16 - 4 = 12
Ответ: значение выражения равно 12
Пример 3:
Найдите значение выражения (4 + 7) * 2 + 6.
Решение:
Сначала выполним операцию в скобках:
4 + 7 = 11
Затем умножим полученное значение на 2:
11 * 2 = 22
Прибавим 6:
22 + 6 = 28
Ответ: значение выражения равно 28
Графическое представление алгебраических выражений

Одним из самых распространенных способов графического представления алгебраических выражений является использование координатной плоскости. На этой плоскости оси X и Y используются для отображения различных переменных и значений. Это может помочь ученикам визуально понять, как изменение значений переменных влияет на результат алгебраического выражения.
Графическое представление также позволяет визуализировать зависимости между переменными и выражениями. Например, линейные выражения представляются на графике в виде прямых линий, а квадратные выражения - в виде парабол. Это помогает ученикам увидеть, какие изменения в формулах и переменных приводят к изменению формы и положения графика.
Графики также могут быть использованы для решения уравнений и систем уравнений. Путем нахождения точек пересечения графиков двух выражений, ученики могут найти значения переменных, при которых уравнения равны между собой.
Использование графического представления алгебраических выражений позволяет ученикам лучше понять и запомнить основные концепции алгебры. Он также обеспечивает визуальный способ решения задач и работы с формулами, что может быть особенно полезным для визуально мыслящих учеников.
Алгебра в повседневной жизни
Первым и, пожалуй, самым очевидным примером применения алгебры в повседневной жизни является расчет финансов. Когда мы составляем бюджет для покупки продуктов, оплачиваем счета за коммунальные услуги или планируем финансовые вложения, мы используем алгебру для решения этих задач. Мы складываем, вычитаем, умножаем и делим числа, применяем принципы пропорции и процентного соотношения, чтобы точно рассчитать наши затраты и доходы.
Алгебра также играет важную роль в строительстве и дизайне. При проектировании и строительстве зданий и сооружений инженеры применяют алгебру для расчета нагрузок, величин и пропорций. Архитекторы используют алгебру для создания эстетически приятных и гармоничных форм, а дизайнеры – для разработки композиций и расчетов пропорций в интерьере и графике.
В медицине алгебра помогает врачам и медсестрам проводить измерения, расчеты дозировок лекарств и создавать различные математические модели для исследования заболеваний и разработки лечебных методов. В физике и химии алгебра используется для построения формул, расчета величин, анализа данных и моделирования различных процессов.
Но алгебра не ограничивается только профессиональными областями. Она очень полезна и в повседневной жизни каждого человека. Знание алгебры позволяет мыслить логически и аналитически, развивает критическое мышление и способность решать сложные задачи. Алгебра обучает нас систематизации, абстрактному мышлению и уверенности в собственных математических навыках.
Таким образом, алгебра является неотъемлемой частью нашей повседневной жизни. Знание и применение алгебры позволяет нам лучше разбираться в мире чисел и формул, решать различные задачи и применять математическую логику во многих сферах деятельности.



