В стереометрии существует несколько основных аксиом, которые лежат в основе геометрических рассуждений. Они определяют взаимное расположение точек, прямых и плоскостей в пространстве.
Первая основная аксиома – это аксиома отношения. Она гласит, что между двумя точками можно провести только одну прямую. Эта аксиома составляет основу для всех геометрических построений и операций. Она означает, что каждая точка в пространстве имеет свое уникальное положение.
Вторая аксиома – аксиома расположения. Она определяет отношение плоскостей в пространстве. Аксиома гласит, что две плоскости либо пересекаются по прямой, либо параллельны друг другу. Это позволяет определять взаимное положение плоскостей и строить трехмерные геометрические объекты.
Роль аксиом в стереометрии
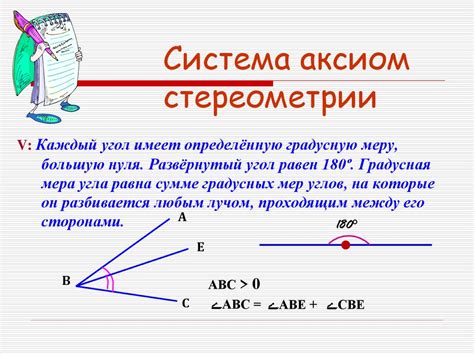
Аксиомы позволяют нам формализовать и упорядочить знания о трехмерном пространстве, делая геометрию стереометрии точной наукой. Они также служат основой для доказательств других математических утверждений в стереометрии. Без аксиом геометрия стереометрии теряет свою системность и точность.
Основные аксиомы стереометрии включают аксиому о существовании прямой, аксиому о существовании плоскости, аксиому о взаимном положении прямой и плоскости, аксиому о существовании прямой, проходящей через две точки, аксиому о взаимном положении двух прямых.
Пример аксиомы:
Аксиома о взаимном положении двух прямых: Через каждые две точки пространства проходит единственная прямая.
Основные понятия стереометрии
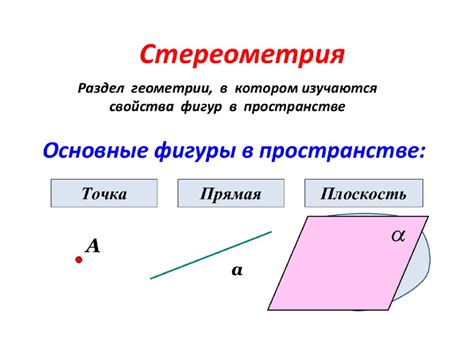
Плоскость – это геометрическое понятие, обозначающее двумерную поверхность, которая не имеет толщины и бесконечна во всех направлениях.
Прямая – это линия, которая не имеет ни начала, ни конца, и простирается в бесконечность в обоих направлениях.
Отрезок – это конечная часть прямой, которая имеет начало и конец.
Угол – это область пространства, ограниченная двумя лучами, имеющими одну общую точку, которая называется вершиной угла.
Треугольник – это фигура, образованная тремя отрезками, которые называются сторонами треугольника, и тремя углами.
Параллельные прямые – это прямые, которые лежат в плоскости и никогда не пересекаются друг с другом.
Правильный многогранный уголник – это трехмерная фигура, у которой все грани и углы равны между собой.
Знание этих основных понятий поможет лучше понять и изучить стереометрию и ее аксиомы.
Основные аксиомы стереометрии

Первая аксиома стереометрии – это аксиома существования. Она утверждает, что существуют такие объекты, как точки, прямые и плоскости. Точка – это элементарный объект, не имеющий размеров. Прямая – это объект, у которого все точки лежат на одной прямой линии. Плоскость – это объект, у которого все точки лежат в одной плоскости.
Вторая аксиома стереометрии – это аксиома равенства. Она утверждает, что если два объекта в стереометрии имеют одинаковый размер или одинаковую форму, то они считаются равными. Это позволяет проводить сравнение размеров и форм объектов.
Третья аксиома стереометрии – это аксиома параллельности. Она утверждает, что через одну точку, не лежащую на данной прямой, можно провести только одну параллельную прямую к данной. Эта аксиома позволяет определить и работать с параллельными линиями и плоскостями.
Четвертая аксиома стереометрии – это аксиома непрерывности. Она утверждает, что любой отрезок может быть продолжен до бесконечности. Эта аксиома позволяет работать с бесконечными линиями и плоскостями.
Пятая аксиома стереометрии – это аксиома отношения. Она утверждает, что между двумя объектами можно построить соотношение, которое определяет их взаимное положение и свойства. Эта аксиома позволяет изучать и анализировать связь между различными объектами в стереометрии.
Примеры применения аксиом в задачах стереометрии

Аксиомы в стереометрии представляют собой набор основных утверждений, которые используются для решения задач по измерению и расчету объемных фигур. С их помощью можно сформулировать основные правила и свойства, которыми руководствуются при решении стереометрических задач.
Применение аксиом в задачах стереометрии позволяет решать разнообразные задачи, связанные с нахождением объемов тел и вычислением их величин. Некоторые примеры применения аксиом в задачах стереометрии:
- Задача на нахождение объема параллелепипеда: Используя аксиому о равенстве объемов, можно сформулировать правило, согласно которому объем параллелепипеда равен произведению длины одной из его сторон на площадь основания.
- Задача на нахождение объема цилиндра: При решении этой задачи можно использовать аксиому о равенстве объемов. Согласно этой аксиоме, объем цилиндра равен произведению площади основания на высоту.
- Задача на нахождение объема пирамиды: Аксиома о равенстве объемов позволяет сформулировать правило, по которому объем пирамиды равен произведению площади основания на высоту, деленное на 3.
Это лишь некоторые примеры использования аксиом в задачах стереометрии. Аксиомы помогают систематизировать и упростить процесс решения задач, позволяют получить точные результаты и установить соответствующие свойства объемных фигур.



