В физике, стандартное отклонение и дисперсия являются важными статистическими понятиями, которые используются для измерения разброса значений вокруг среднего значения. Они помогают оценить стабильность и точность экспериментальных данных, что крайне важно в научных исследованиях. В этой статье мы рассмотрим, как определить стандартное отклонение и дисперсию, а также приведем некоторые примеры их применения в физических измерениях.
Стандартное отклонение (или среднеквадратическое отклонение) показывает, насколько значения измеряемой величины различаются от ее среднего значения. Оно вычисляется путем нахождения среднего квадратического значения отклонений каждого значения от среднего значения. Большое стандартное отклонение указывает на большой разброс значений в выборке, а маленькое значение – на небольшие отличия от среднего значения.
Дисперсия – это квадрат стандартного отклонения. Это мера разброса значений и также позволяет определить точность среднего значения величины. Чем меньше дисперсия, тем более стабильны и точны измеренные значения. Дисперсия вычисляется как среднее квадратическое отклоние значений от среднего значения, возведенное в квадрат.
Определение стандартного отклонения и дисперсии в физике
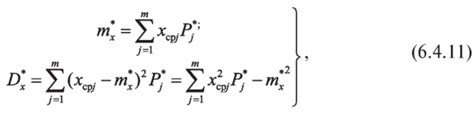
Стандартное отклонение (σ) представляет собой меру разброса значений относительно среднего. Оно вычисляется как корень квадратный из дисперсии. Чем больше стандартное отклонение, тем больше разброс значений и наоборот.
Дисперсия (σ²) - это среднее квадратов отклонений каждого значения от среднего значения. Она показывает, насколько сильно значения разбросаны вокруг среднего значения. Чем больше дисперсия, тем больше разница между значениями и средним значением.
В физике стандартное отклонение и дисперсия используются для анализа результатов экспериментов и измерений. Например, в эксперименте, где измеряется время свободного падения тела, стандартное отклонение и дисперсия позволяют оценить, насколько точны полученные значения. Чем меньше стандартное отклонение, тем более точны и согласованы результаты измерений. Это значит, что эксперимент можно считать более надежным и точным.
Использование стандартного отклонения и дисперсии в физике позволяет анализировать результаты экспериментов, выявлять причины ошибок и улучшать точность измерений. Они помогают установить степень разброса значений и определить стабильность и достоверность полученных данных.
Что такое стандартное отклонение?

Стандартное отклонение вычисляется как квадратный корень из дисперсии. Дисперсия, в свою очередь, является средним квадратическим отклонением каждого значения из выборки от её среднего значения.
Стандартное отклонение позволяет оценить, насколько точно среднее значение представляет выборку или группу данных. Чем меньше стандартное отклонение, тем ближе значения к среднему. Величина стандартного отклонения также позволяет сравнивать разброс между различными выборками или группами данных.
Стандартное отклонение в физике используется для измерения разброса значений физических величин, таких как скорость, температура или масса. Например, если мы измеряем скорость движения объекта в нескольких экспериментах, то стандартное отклонение позволяет нам оценить, насколько точные наши измерения.
Кроме того, стандартное отклонение используется для анализа результатов множества измерений или экспериментов. Например, если у нас есть набор результатов измерения давления в различных точках, то стандартное отклонение позволяет определить, насколько велик разброс значений и насколько надёжны наши измерения.
Итак, стандартное отклонение является одним из ключевых показателей разброса значений в выборке или группе данных. Оно позволяет оценить точность и надёжность измерений, а также сравнивать различные выборки или группы данных.
Что такое дисперсия?
Дисперсию обычно обозначают символом σ2. Чтобы рассчитать дисперсию, нужно вычислить сумму квадратов отклонений каждого значения в наборе данных от его среднего значения и разделить эту сумму на количество значений в наборе данных.
Для более наглядного понимания давайте рассмотрим пример. Предположим, у нас есть набор данных, состоящий из следующих значений:
| Значение | Отклонение от среднего значения | Квадрат отклонения |
|---|---|---|
| 5 | -2 | 4 |
| 8 | 1 | 1 |
| 10 | 3 | 9 |
| 4 | -3 | 9 |
| 6 | -1 | 1 |
В данном случае, среднее значение равно 6. Значения во второй колонке таблицы показывают отклонение каждого значения от среднего значения, а значения в третьей колонке - квадраты этих отклонений.
Чтобы рассчитать дисперсию, нужно сложить все значения в третьей колонке и разделить полученную сумму на количество значений в наборе данных. В нашем случае:
σ2 = (4 + 1 + 9 + 9 + 1) / 5 = 24 / 5 = 4.8
Таким образом, дисперсия набора данных равна 4.8.
Дисперсия имеет несколько важных свойств. Во-первых, она всегда будет неотрицательной величиной, так как включает суммы квадратов отклонений. Во-вторых, дисперсия измеряется в квадратных единицах исходных данных. Например, если исходные данные имеют размерность метров, то дисперсия будет иметь размерность метров в квадрате.
Дисперсия является важным понятием в физике и используется для анализа различных физических явлений, таких как случайные отклонения, шумы и многое другое.
Формулы расчета стандартного отклонения и дисперсии
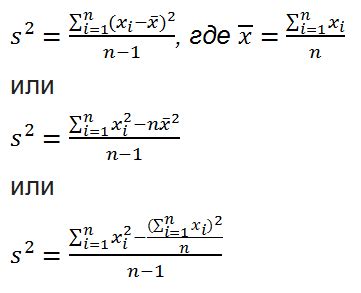
Стандартное отклонение и дисперсия связаны между собой:
Стандартное отклонение (σ) - это положительное квадратное корень из дисперсии. Используется для измерения разброса значений в наборе данных относительно среднего значения. Формула расчета стандартного отклонения:
σ = √((Σ(xi - x̄)^2) / N)
где:
- σ - стандартное отклонение
- Σ - сумма всех значений
- xi - каждое отдельное значение
- x̄ - среднее арифметическое значение
- N - количество значений в наборе данных
Дисперсия (σ^2) - это среднее значение квадратов отклонений от среднего значения. Используется для оценки степени разброса данных. Формула расчета дисперсии:
σ^2 = Σ((xi - x̄)^2) / N
где:
- σ^2 - дисперсия
- Σ - сумма всех значений
- xi - каждое отдельное значение
- x̄ - среднее арифметическое значение
- N - количество значений в наборе данных
Эти формулы позволяют рассчитать стандартное отклонение и дисперсию для любого набора данных. Они являются важными инструментами для анализа физических явлений и обеспечивают точные числовые меры разброса и распределения данных.
Формула для расчета стандартного отклонения

Формула для расчета стандартного отклонения, также известного как среднеквадратическое отклонение, является квадратным корнем из дисперсии. Дисперсия вычисляется путем нахождения среднего квадратичного отклонения от среднего значения. Это позволяет определить, насколько различаются значения измерений от среднего значения.
Математически формулу для расчета стандартного отклонения можно записать следующим образом:
σ = √((Σ(X - μ)²) / N)
Где:
- σ - стандартное отклонение
- Σ - сумма
- X - отдельное значение
- μ - среднее значение
- N - количество значений
Расчет стандартного отклонения требует знания значений всех измерений, среднего значения и их количества. Этот параметр позволяет оценить разброс данных и использовать в физике для анализа неопределенности измерений, оценки точности и сравнения результатов разных опытов.
Формула для расчета дисперсии

Формула для расчета дисперсии задается следующим образом:
| $D = \frac{1}{N} \sum_{i=1}^{N}(X_i - \overline{X})^2$ |
Где:
- $D$ - дисперсия;
- $N$ - количество значений измеряемой величины;
- $X_i$ - значение измеряемой величины;
- $\overline{X}$ - среднее значение измеряемой величины.
Расчет дисперсии состоит из нескольких шагов. Сначала находим среднее значение измеряемой величины. Затем для каждого значения вычитаем среднее и получаем разность. Квадрат каждой разности суммируется. Затем сумма квадратов разностей делится на количество значений измеряемой величины. Итоговое значение является дисперсией.
Формула для расчета дисперсии позволяет получить числовое значение, которое отражает степень разброса данных. Большая дисперсия указывает на большой разброс, а маленькая дисперсия - на маленький разброс значений измеряемой величины относительно их среднего значения.
Примеры использования стандартного отклонения и дисперсии в физике
Приведем несколько примеров использования стандартного отклонения и дисперсии в физике:
| Пример | Описание |
|---|---|
| Измерение времени реакции | При измерении времени реакции человека на некоторый стимул, стандартное отклонение позволяет определить, насколько среднее значение времени реакции отклоняется от значения, которое можно считать типичным. Более высокое стандартное отклонение указывает на большую вариацию времени реакции, что может свидетельствовать о неопределенности в результатах. |
| Измерение массы объекта | При измерении массы объекта с использованием разных инструментов и методов, стандартное отклонение позволяет сравнить точность каждого измерения. Меньшее стандартное отклонение указывает на более точное измерение. Дисперсия же показывает разброс в значениях массы, что может быть полезно для оценки ее стабильности и однородности. |
| Измерение температуры | При измерении температуры в определенных условиях, стандартное отклонение может показать, насколько различаются измерения в разное время. Это поможет определить, насколько стабильны условия эксперимента и какие факторы могут влиять на точность измерений в течение времени. |
Таким образом, стандартное отклонение и дисперсия являются важными инструментами для анализа данных в физике. Они помогают выявить вариации и неопределенности в измерениях, а также оценить точность и надежность экспериментальных результатов.
Пример 1: Измерение времени движения шарика

Представим, что у нас есть эксперимент, в котором мы хотим измерить время движения шарика по наклонной плоскости. Для этого мы проводим несколько измерений и получаем следующие результаты:
- Измерение 1: 2.3 секунды
- Измерение 2: 2.5 секунды
- Измерение 3: 2.4 секунды
- Измерение 4: 2.6 секунды
- Измерение 5: 2.3 секунды
Чтобы найти среднее значение времени движения, мы складываем все результаты и делим их на общее количество измерений. В данном случае:
(2.3 + 2.5 + 2.4 + 2.6 + 2.3) / 5 = 2.42 секунды
Среднее значение времени движения шарика составляет 2.42 секунды. Теперь мы можем найти отклонение каждого измерения от среднего значения. Для этого мы вычитаем среднее значение из каждого измерения и возводим результат в квадрат:
- (2.3 - 2.42)^2 = 0.0124
- (2.5 - 2.42)^2 = 0.0064
- (2.4 - 2.42)^2 = 0.0004
- (2.6 - 2.42)^2 = 0.0324
- (2.3 - 2.42)^2 = 0.0124
Затем мы суммируем все полученные значения и делим их на количество измерений минус одно (в данном случае, 5 - 1 = 4). Таким образом:
(0.0124 + 0.0064 + 0.0004 + 0.0324 + 0.0124) / 4 = 0.01645 секунды
Полученное значение является дисперсией времени движения шарика по наклонной плоскости. Для получения стандартного отклонения, мы извлекаем квадратный корень из дисперсии:
√(0.01645) ≈ 0.128 секунды
Таким образом, стандартное отклонение времени движения шарика составляет примерно 0.128 секунды. Это значение позволяет нам оценить разброс результатов измерений и определить точность нашего эксперимента.
Пример 2: Измерение силы притяжения между двумя телами
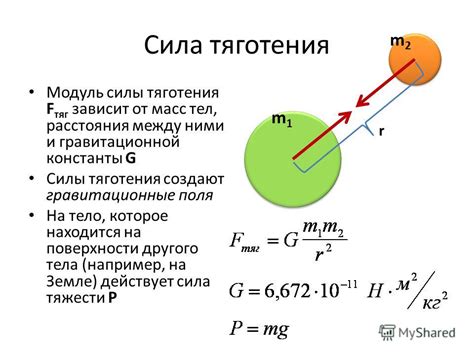
Предположим, что у нас есть два тела массой 1 кг и 2 кг, расположенных на расстоянии 1 м друг от друга. Как измерить силу притяжения между этими телами?
- Измерим расстояние между телами. Для этого возьмем измерительную линейку и поместим ее между телами так, чтобы начало линейки совпадало с положением первого тела, а конец линейки - с положением второго тела. Определим значение расстояния в метрах.
- Измерим массу каждого тела. Весы помогут нам определить массу каждого тела в килограммах.
- Рассчитаем силу притяжения между телами с помощью закона всемирного тяготения: сила притяжения равна произведению масс каждого тела и обратно пропорциональна квадрату расстояния между ними. Математически это записывается в виде формулы F = G * (m1 * m2) / r^2, где F - сила притяжения, G - гравитационная постоянная, m1 и m2 - массы тел, r - расстояние между телами.
- Подставим измеренные значения массы и расстояния в формулу и рассчитаем силу притяжения. Например, если масса первого тела равна 1 кг, масса второго тела равна 2 кг, а расстояние между ними равно 1 м, то сила притяжения будет равна F = G * (1 кг * 2 кг) / (1 м)^2
Таким образом, измерение силы притяжения между двумя телами в физике может быть осуществлено с помощью измерения расстояния между телами, измерения их массы и применения соответствующей формулы.



