Производная функции – это одна из фундаментальных концепций математического анализа, которая позволяет понять изменение функции в окрестности заданной точки. Она показывает, как меняется значение функции при малых изменениях входного параметра в данной точке.
Производная функции в точке x можно интерпретировать как тангенс угла наклона касательной к графику функции в этой точке. Благодаря этому свойству, производная имеет множество практических применений: от нахождения экстремумов функции до определения скорости изменения величин в различных областях науки и техники.
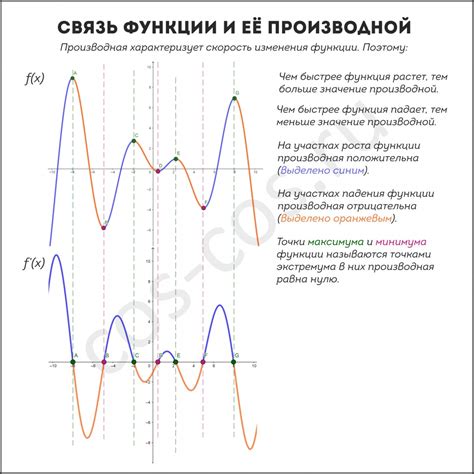
Производная функции в точке x может быть положительной, отрицательной или равной нулю. Если производная положительна, то функция возрастает в этой точке. Если производная отрицательна, то функция убывает в этой точке. А если производная равна нулю, то функция имеет экстремум – либо локальный минимум, либо локальный максимум.
Важно отметить, что производная функции является функцией сама по себе. Это означает, что она может меняться в разных точках графика и, следовательно, позволяет нам анализировать поведение функции во всем ее области определения.
Производная функции и ее значение
Производная функции в точке x обозначается как f'(x) или dy/dx. Она определяется как предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
f'(x) = lim Δx→0 (f(x + Δx) - f(x)) / Δx
Значение производной функции в точке x имеет особую интерпретацию. Если производная положительна, то функция возрастает в данной точке. Если производная отрицательна, то функция убывает. А если производная равна нулю, то в данной точке может быть экстремум функции (максимум или минимум).
Понимание производной и ее значения позволяет решать различные задачи, связанные с изучением функций. Например, можно найти точки перегиба, асимптоты, а также определить поведение функции вблизи интересующей нас точки.
Изучение производных функций и их значений является одним из основных элементов математического анализа и находит практическое применение в различных областях, таких как физика, экономика и технические науки.
Определение и основные понятия
Для понимания того, что показывает производная функции в точке x, необходимо знать несколько основных понятий:
- Производная функции - это показатель изменения функции в зависимости от изменения аргумента. Математически обозначается как f'(x) или dy/dx.
- Точка - это конкретное значение аргумента функции, в которой мы рассчитываем производную.
- Наклон касательной - это значение производной функции в точке x. Он определяет угол наклона касательной к графику функции в данной точке.
- Тангенс угла наклона касательной - это отношение прилежащего катета (изменение значения функции) к противолежащему катету (изменение значения аргумента). Он равен значению производной функции в точке x.
Эти понятия являются основополагающими при исследовании функций и рассмотрении их производных в конкретных точках. Показатель значения производной функции в точке x позволяет увидеть, как функция изменяется в данной точке и каков наклон касательной к ее графику.
Точка экстремума и производная
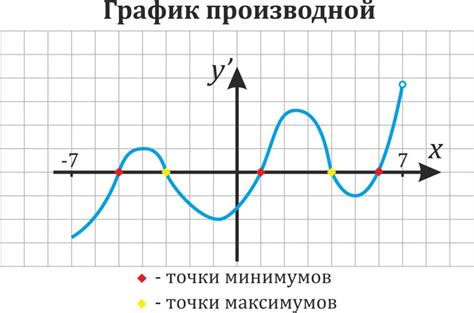
Точка экстремума функции - это точка, в которой функция достигает локального минимума или максимума. Для определения точек экстремума используется производная функции.
Если производная функции в точке x равна нулю, то это может означать, что функция имеет локальный максимум или минимум в этой точке. Однако, это не является достаточным условием. Для более точного определения типа экстремума необходимо проанализировать значение второй производной функции в данной точке. Если вторая производная положительна, то это указывает на локальный минимум, а если она отрицательна - на локальный максимум.
Таким образом, производная функции в точке x позволяет нам определить наличие и тип точки экстремума. Это очень важное свойство производной, которое активно используется в математическом анализе и оптимизации функций.
Производная и изменение функции в окрестности точки

Пусть у нас есть функция f(x), которая дифференцируема в некоторой окрестности точки x. Производная функции в точке x, обозначаемая как f'(x) или dy/dx, определяется как предел отношения приращения функции к приращению аргумента при стремлении этого приращения к нулю. Математически это можно записать следующим образом:
| f'(x) = limh→0 (f(x + h) - f(x))/h |
Если производная функции в точке x положительна, то это означает, что функция возрастает в окрестности данной точки. Если производная отрицательна, то функция убывает. Если же производная равна нулю, то функция может иметь экстремум в данной точке.
Производная функции также позволяет определить форму графика функции в окрестности точки x. Если производная положительна на всей окрестности х, то график функции будет возрастающим. Если же производная отрицательна на всей окрестности х, то график функции будет убывающим. Если производная чередуется с положительными и отрицательными значениями, то график функции будет иметь точку перегиба.
Таким образом, производная функции в точке x является важной характеристикой её изменения и позволяет определить множество особенностей графика функции в окрестности данной точки.
Производная и направление изменения функции

Производная функции в точке x показывает направление изменения значения функции при изменении аргумента в этой точке.
Если производная положительна, то функция возрастает в данной точке, то есть значения функции увеличиваются при увеличении аргумента.
Если производная отрицательна, то функция убывает в данной точке, то есть значения функции уменьшаются при увеличении аргумента.
Если производная равна нулю, то у функции может быть экстремум в данной точке: максимум или минимум.
Также производная позволяет определить выпуклость или вогнутость функции. Если производная увеличивается при увеличении аргумента, то функция выпукла в данной точке. Если производная уменьшается при увеличении аргумента, то функция вогнута.
Таблица ниже показывает, какие значения производной свидетельствуют о разных направлениях изменения функции:
| Значение производной | Направление изменения функции |
|---|---|
| Положительное | Возрастание |
| Отрицательное | Убывание |
| Нулевое | Экстремум |
Производная и геометрическая интерпретация

Производная функции в точке x представляет собой мгновенную скорость изменения функции в этой точке. Иначе говоря, она показывает, как быстро функция меняет свое значение при изменении аргумента.
Геометрически, производная функции в точке x может быть интерпретирована как угловой коэффициент касательной к графику функции в этой точке. Если значение производной положительно, значит график функции в данной точке возрастает, а если значение производной отрицательно - график функции в данной точке убывает. Если значение производной равно нулю, то график функции имеет экстремум - максимум или минимум.
Если производная функции в точке x не существует, это может означать, что график функции имеет разрыв в этой точке, вертикальную асимптоту или касательную горизонтальной.
Производная и кривизна графика функции
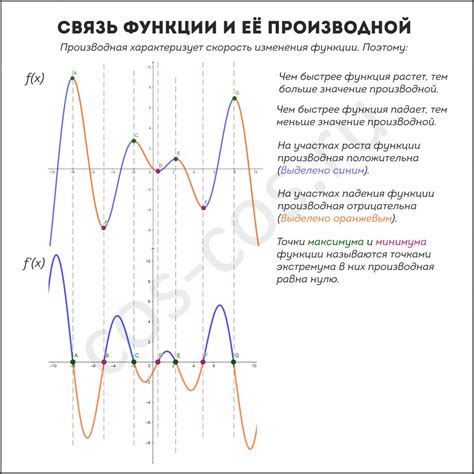
Производная функции в точке x показывает скорость изменения функции в этой точке. Однако, производная также дает информацию о кривизне графика функции.
Если производная функции положительна в точке x, то это означает, что функция в этой точке возрастает. График функции будет иметь положительный наклон.
Если производная функции отрицательна в точке x, то функция в этой точке убывает. График функции будет иметь отрицательный наклон.
Если производная функции равна нулю в точке x, то функция достигает экстремума в этой точке. Это может быть локальный минимум или максимум. График функции будет иметь горизонтальный наклон.
Кривизна графика функции может быть определена с помощью второй производной. Если вторая производная положительна, то график функции будет выпуклым вверх (иметь положительную кривизну). Если вторая производная отрицательна, то график функции будет выпуклым вниз (иметь отрицательную кривизну). Если вторая производная равна нулю, то график функции будет иметь точку перегиба.
| Знак производной | Наклон графика | Кривизна графика |
|---|---|---|
| Положительный | Возрастает | Положительная |
| Отрицательный | Убывает | Отрицательная |
| Ноль | Горизонтальный | Точка перегиба |
Производная и поиск точек разрыва функции
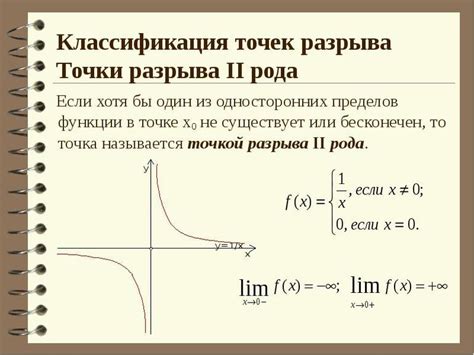
Для поиска точек разрыва функции мы можем использовать производную функции. Если производная функции имеет разрыв в точке x, то это может означать, что функция также имеет разрыв или особенность в этой точке.
Существует несколько типов точек разрыва: точка разрыва первого рода, точка разрыва второго рода и изолированная точка разрыва. Точка разрыва первого рода - это точка, в которой левосторонний и правосторонний пределы функции отличаются или один из них не существует. Точка разрыва второго рода - это точка, в которой пределы функции существуют, но не равны между собой или не равны значению функции в этой точке. Изолированная точка разрыва - это точка, в которой функция не определена только в одной точке, а в остальных точках она непрерывна.
Для определения точек разрыва функции, мы можем проанализировать производную функции и найти значения x, которые приводят к разрыву производной. Эти значения x будут являться точками разрыва функции. Для этого мы можем использовать такие методы, как нахождение значений x, при которых производная равна бесконечности или не существует, или нахождение значений x, при которых производная меняет знак с отрицательного на положительный или наоборот.
Исследование точек разрыва функции является важным шагом в понимании ее свойств и поведения. Это помогает нам определить, когда функция может иметь локальный или глобальный экстремум, точки перегиба и другие интересные особенности.
Производная и приближенный расчет функции

Однако, иногда мы можем столкнуться с ситуацией, когда аналитическая формула для вычисления производной функции оказывается слишком сложной или неизвестной. В таких случаях мы можем использовать приближенные методы расчета производной.
Одним из таких методов является метод конечных разностей. Он основан на аппроксимации производной с помощью разделенной разности, вычисленной на небольшом интервале h.
Формула для приближенного расчета производной функции в точке x выглядит следующим образом:
f'(x) ≈ (f(x + h) - f(x)) / h
Здесь f'(x) - приближенное значение производной функции в точке x, f(x) - значение функции в точке x, h - маленькое изменение аргумента.
Чем меньше значение h, тем точнее будет приближение производной. Однако, слишком маленькое значение h может привести к ошибкам округления при вычислениях. Поэтому значение h выбирают достаточно малым, но не слишком малым.
Обратите внимание, что метод конечных разностей является приближенным и не всегда точным. Он применяется в случаях, когда аналитическое вычисление производной затруднено или невозможно.
Производная и решение задач оптимизации

Производная функции позволяет определить, где функция достигает своего минимума или максимума. В точках, где производная равна нулю или не существует, функция может иметь точки экстремума. Это могут быть точки минимума (когда производная меняется с отрицательной на положительную) или точки максимума (когда производная меняется с положительной на отрицательную).
Кроме того, производная может помочь найти точки перегиба функции. Точки перегиба - это точки, в которых вторая производная изменяет свой знак. Такие точки служат важным ориентиром для оптимизации функции.
Если задача оптимизации требует поиска наилучшего значения, можно использовать производные для определения границ области, в которой находится оптимальное решение. К примеру, если функция гладкая и выпуклая вверх, то оптимальное значение будет достигаться на границе данной области.
Важно отметить, что производная функции является локальной характеристикой функции и может не давать полной информации о глобальной оптимальности. Поэтому, при решении задач оптимизации необходимо учитывать также другие факторы и ограничения.



