Тема бесконечности и ее свойств вызывает неоспоримый интерес как среди математиков, так и среди философов. В случае, когда мы говорим о результате умножения бесконечности на бесконечность, мы сталкиваемся с интересными ограничениями и особенностями.
Представление бесконечности в математике порождает некоторые противоречия и вызывает неоднозначность. Однако, понятие умножения бесконечности на бесконечность предлагает рассмотреть эту проблему с новой стороны и найти решение с помощью математических методов и концепций.
При обсуждении умножения бесконечности на бесконечность важно быть осторожным и учитывать специфику бесконечности как математического объекта. Верно ли, что результатом умножения двух бесконечностей является бесконечность? Или же мы можем получить более сложный результат, который требует более глубокого анализа и понимания?
Что такое бесконечность?

В математике, бесконечность может иметь разные формы и свойства. Она может быть положительной или отрицательной, конечной или бесконечной. Бесконечность также может быть предельной или абсолютной.
Бесконечность можно представить как продолжение числовой шкалы в обоих направлениях до бесконечности. Это означает, что любое число можно бесконечно увеличивать или уменьшать, не достигая предела.
- Бесконечность часто используется в математике для обозначения бесконечных последовательностей и рядов чисел.
- Бесконечность также встречается в физике, где она используется для описания неконечно малых и неконечно больших величин.
- Бесконечность является абстрактным понятием, которое помогает нам понять и описать мир вокруг нас на более глубоком уровне.
Важно отметить, что операции с бесконечностью могут иметь определенные особенности и ограничения. Например, результат умножения бесконечности на бесконечность не всегда определен и может зависеть от контекста и использованных правил.
Каким образом производится умножение бесконечности на бесконечность?
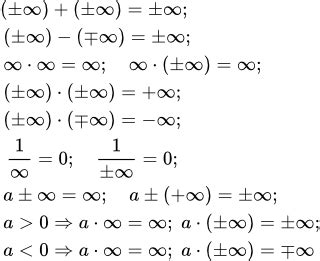
Для начала, стоит отметить, что бесконечность - это не число в строгом смысле этого понятия. Она является более абстрактным и неопределенным понятием. Поэтому, когда говорят о произведении двух бесконечностей, имеют в виду некоторые особенности исключительно математической модели.
В некоторых случаях, умножение бесконечности на бесконечность может быть представлено как некоторая форма "бесконечность на 1". Например, если рассмотреть предел функции, которая стремится к бесконечности при возрастании аргумента, то можно получить результат "бесконечность на 1". Однако, в контексте обычных числовых операций, такое умножение не имеет определенного значения.
Однако, следует заметить, что умножение бесконечности на бесконечность обычно рассматривается в контексте математического анализа, где рассматриваются пределы функций, ряды и другие математические объекты. В этих контекстах формулируются определенные правила и условия, согласно которым можно проводить операции с бесконечностями.
Итак, умножение бесконечности на бесконечность не имеет общего определенного значения в контексте обычных числовых операций. Однако, в математическом анализе существуют определенные правила и условия, при которых можно говорить о произведении бесконечностей, и которые позволяют добиться определенных результатов.
Возможные варианты результата умножения

Один из возможных вариантов результата умножения бесконечности на бесконечность - это бесконечность. В некоторых моделях, таких как расширенная комплексная плоскость или супердействительные числа, произведение бесконечностей может быть определено как бесконечность. Это означает, что умножение двух бесконечностей приводит к сохранению бесконечности.
Однако, в других моделях, результатом умножения бесконечности на бесконечность может быть неопределенность или бесконечно малая величина. В таких случаях, произведение двух бесконечностей может быть неопределенным или неограниченным.
Также стоит отметить, что результат умножения бесконечности на бесконечность может зависеть от порядка операндов. В некоторых моделях, результат может быть разным в зависимости от того, какую из бесконечностей считать первым множителем.
В любом случае, результат умножения бесконечности на бесконечность всегда будет специальным и будет зависеть от выбранной математической модели. Именно поэтому в классической математике, где бесконечность не является числом, операция умножения бесконечностей не имеет определенного значения.
| Теория | Результат умножения |
|---|---|
| Расширенная комплексная плоскость | Бесконечность |
| Супердействительные числа | Бесконечность |
| Нестандартный анализ | Неопределенность |
| Теория меры | Неограниченность или бесконечно малая величина |
Арифметические особенности при умножении бесконечности на бесконечность

В математике бесконечность - это не конкретное число, а скорее понятие, означающее бесконечно большое значение. В зависимости от контекста, бесконечность может представляться разными способами, например, положительной или отрицательной, бесконечностью по модулю или бесковариантностью.
Если сколько-нибудь умножить бесконечность на бесконечность, то результат может быть разным в зависимости от правил, принятых в арифметике. В некоторых случаях результатом может быть бесконечность большая, чем исходные значения, а в других случаях бесконечность может оказаться меньшей или даже равной исходным значениям.
Один из способов работы с такой арифметической операцией - это использование понятия "бесконечно малого". В этом случае результатом умножения бесконечности на бесконечность будет бесконечно малое значение, которое можно считать эквивалентным нулю. Это позволяет избежать неопределенностей и упростить дальнейшие математические выкладки.
Таким образом, умножение бесконечности на бесконечность - это неоднозначная операция, требующая внимательного рассмотрения и правильного выбора используемых математических правил. В зависимости от контекста и особенностей задачи, результатом может быть различное значение, и только точное определение используемых правил позволит получить корректный результат.
Некорректные рассуждения о результате умножения бесконечности на бесконечность

Некоторые люди могут сделать ошибочные предположения о результате такого умножения. Одним из них является утверждение, что результатом будет бесконечность. Однако, это утверждение неверно, поскольку мы не можем применить обычные алгебраические правила к бесконечностям. Бесконечность - это не число, а концепция, обозначающая отсутствие ограничений или бесконечно большой размер.
Другим неправильным рассуждением является утверждение, что результатом будет ноль. Это также неверно, поскольку умножение бесконечности на ноль не имеет определения в математике. Умножение числа на бесконечность даёт смысленный результат, но это не относится к умножению бесконечности на бесконечность.
Следует отметить, что умножение бесконечности на конечное число, как и любые другие арифметические операции с бесконечностями, требует особых расчетных правил и подходов, которые используются в математическом анализе. Это область, изучающая пределы и бесконечности, и она имеет свои специфические методы работы.
Математические теории и определения, связанные с умножением бесконечности на бесконечность

Одной из таких теорий является теория пределов. Согласно этой теории, умножение бесконечности на бесконечность может давать различные результаты в зависимости от формы бесконечностей, которые участвуют в операции. Например, если обе бесконечности являются положительными и одинаково направленными, то результатом умножения будет положительная бесконечность. Если же бесконечности являются противоположно направленными, то результатом будет отрицательная бесконечность. Если же одна из бесконечностей является положительной, а другая - отрицательной, то результатом будет отрицательная бесконечность.
Еще одной теорией, которая связана с умножением бесконечности на бесконечность, является теория бесконечно малых. Если одна из бесконечностей является бесконечно малой, а другая - бесконечностью, то результатом умножения будет бесконечно малая величина. Такое умножение может быть использовано при решении задач математического анализа и физики.
Также стоит упомянуть о теории бесконечно больших функций. В рамках этой теории существуют определенные правила, которые позволяют определить результат умножение различных бесконечностей. Например, результат умножения бесконечности на нуль будет равен нулю. Такие правила помогают упростить вычисления и анализ при работе с бесконечностями.
Все эти математические теории и определения позволяют лучше понять особенности операции умножения бесконечности на бесконечность и применить их при решении различных математических задач.
Примеры применения умножения бесконечности на бесконечность в различных науках

Умножение бесконечности на бесконечность часто встречается в различных научных областях и может иметь различные интерпретации в зависимости от контекста.
1. Математика: В математике, умножение бесконечности на бесконечность не имеет однозначного результата. В некоторых случаях, результатом такой операции может быть бесконечность, но в других случаях результат может быть неопределенным или даже конечным числом.
2. Физика: В физике, умножение бесконечности на бесконечность может использоваться для расчета предельных значений или для описания бесконечно малых или бесконечно больших величин. Например, при расчете предельных значений функций или при описании бесконечно удаленных объектов в космологии.
3. Инженерия: В инженерии, умножение бесконечности на бесконечность может применяться для анализа сложных систем, где одна переменная или параметр стремится к бесконечности, тогда как другая переменная или параметр также стремится к бесконечности. Это может помочь инженерам определить предельные значения или оценить поведение системы в экстремальных условиях.
4. Экономика: В экономике, умножение бесконечности на бесконечность может использоваться для расчета предельных значений производства или потребления, а также для анализа экономического роста. Например, в моделях роста экономики, бесконечность может представлять бесконечный рост производства или дохода.
5. Нейронаука: В нейронауке, умножение бесконечности на бесконечность может быть использовано для моделирования сложных нейронных сетей или для определения предельных значений в проблемах синаптической пластичности. Например, это может быть связано с устойчивостью нейронных сетей или с определением предельной пропускной способности для передачи информации.
Применение умножения бесконечности на бесконечность в различных науках может варьироваться в зависимости от контекста и задачи, которую необходимо решить. Такое использование может быть полезным для анализа предельных значений, расчета бесконечно малых или бесконечно больших величин, а также для моделирования сложных систем.
Философские аспекты результатов умножения бесконечности на бесконечность

Умножение бесконечности на бесконечность предлагает еще более интересные философские проблемы. Что произойдет, если бесконечное количество элементов будет умножено на другое бесконечное количество элементов? Какой будет результат этой операции? Можно ли вообще продолжать операции с бесконечностями, и если да, то какие законы и правила будут действовать?
Одна из возможных интерпретаций результатов умножения бесконечности на бесконечность связана с идеей о бесконечности, как о целостности и неограниченности всего сущего. В этом контексте результат может быть воспринят как повышенная форма бесконечности, расширяющая представление о бесконечности и превосходящая любые человеческие пределы и ограничения.
В то же время, рассмотрение результатов умножения бесконечности на бесконечность может привести к параллелям с теорией множеств и понятием бесконечного множества. Эти параллели могут иметь глубокие последствия для понимания самой природы бесконечности и ее связи с математическими и философскими концепциями.
Однако, следует отметить, что умножение бесконечности на бесконечность также может привести к проблемам и парадоксам, связанным с бесконечными и неопределенными значениями. Некоторые философы и математики утверждают, что результат такого умножения не может быть определен и имеет более сложную природу, выходящую за рамки обычного понимания.
Окончательное решение философских аспектов результатов умножения бесконечности на бесконечность все еще представляет вызов для нас. Каждая интерпретация и подход может дать новые представления и полезные инсайты в саму природу бесконечности. Важно проявлять гибкость в мышлении и не ограничиваться одной точкой зрения, чтобы полностью исследовать все философские аспекты этой уникальной и сложной проблемы.



