Понятие бесконечности вызывает великое удивление и множество вопросов. Что происходит, когда мы пытаемся вычитать бесконечность из бесконечности? Можно ли вообще выполнить такую операцию? Давайте разберемся.
Изначально надо сказать, что бесконечность не является числом в обычном смысле этого слова. Это абстрактное понятие, которое олицетворяет неограниченность. Поэтому представить себе вычитание бесконечности из бесконечности достаточно сложно.
Можно определить такие ситуации в математике, когда результатом вычитания бесконечности из бесконечности будет близость к определенному числу или бесконечность. Однако, это уже условная модель и не соответствует реальности. Такие неопределенности говорят о том, что нам нужно более точно определить условия задачи или применить другие методы решения.
Определение бесконечности
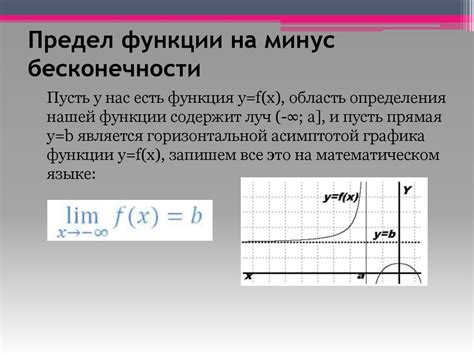
В математике существует два типа бесконечности: положительная и отрицательная. Положительная бесконечность обозначается символом "∞" и представляет бесконечно большое положительное число. Отрицательная бесконечность, обозначаемая символом "-∞", представляет бесконечно малое отрицательное число.
Вычитание бесконечности из бесконечности является неопределенной операцией. В различных математических теориях могут быть предложены разные способы обработки этого типа операций, но они затрагивают математические понятия и концепции, выходящие за рамки этой статьи.
Однако, в простейшем случае, когда мы вычитаем положительную бесконечность из положительной бесконечности, результат может быть определен как некоторая форма неопределенности или бесконечность. Это связано с тем, что бесконечность не подчиняется обычным правилам арифметики и не может быть точно определена или выражена числовым значением.
Таким образом, вычитание бесконечности из бесконечности остается сложной и неоднозначной операцией. Это напоминает нам о том, что бесконечность является абстрактным понятием, которое не всегда можно представить точным числом или значением.
Как мы представляем бесконечность

Однако, несмотря на то, что бесконечность может показаться нам необъятной и непостижимой, она активно используется в математике и физике для решения сложных задач. В математике, когда мы вычитаем одну бесконечность из другой, хотя это звучит парадоксально, мы можем получить определенные полезные результаты.
Идея бесконечности также присутствует в некоторых философских и религиозных учениях. Возникает вопрос: что находится за границами нашей вселенной? Может ли существовать что-то вне пространства и времени? Ответы на эти вопросы до сих пор остаются загадкой.
Когда мы пытаемся представить бесконечность, наш мозг может испытывать затруднения. Он не приспособлен для восприятия бесконечности, так как мы живем в ограниченном мире, где все имеет начало и конец. Но именно эта неспособность представить себе бесконечность побуждает нас стремиться к познанию и открытиям, чтобы проникнуть в тайны бесконечного мира.
Таким образом, представление о бесконечности оставляет много вопросов без ответа, вызывает чувство удивления и восхищения перед необъятностью Вселенной. Бесконечность пронизывает наш мир и стимулирует наш разум к поиску нового знания и пониманию мира вокруг нас.
Арифметические операции с бесконечностью

Когда мы вычитаем бесконечность из бесконечности, результат может быть неопределенным или не существовать. Такая операция представляет собой форму неопределенности, которая требует дополнительных условий для определения.
Например, если у нас есть выражение ∞ - ∞, мы можем получить разные результаты в зависимости от конкретной ситуации. В некоторых случаях результат может быть равен нулю, в других - бесконечности.
В математике также существуют правила и определения, которые могут помочь определить результат арифметических операций с бесконечностью. Например, правило L'Hôpital'a позволяет вычислять пределы функций, в которых встречаются бесконечности.
Учитывайте, что арифметика с бесконечностью является сложной и нетривиальной областью математики, требующей внимательного и аккуратного рассмотрения в каждом конкретном случае.
Сложение бесконечности

В рамках классической математики, сложение бесконечностей не определено, поскольку мы не можем однозначно определить, что получится в результате такой операции. Как правило, в математической терминологии исключение составляет случай, когда мы имеем дело с реально бесконечным множеством элементов, например, множеством всех натуральных чисел.
Однако, в более абстрактных математических теориях и расширенных системах, таких как теория множеств или теория чисел, сложение бесконечности может иметь определенные значения или свойства. Например, в ряде случаев сложение двух бесконечностей может привести к получению большей бесконечности или оставаться неопределенным, что зависит от контекста и используемых аксиоматических систем.
Все это отражает сложность понятия бесконечности и неоднозначность его математического рассмотрения. Сложение бесконечности требует специального подхода и не всегда может быть легко интерпретировано или аналитически вычислено.
Умножение бесконечности

Когда мы умножаем бесконечность на некоторое число, результатом является бесконечность. Это можно представить как увеличение числа на бесконечность, что не имеет конечного результата.
Однако умножение бесконечности на бесконечность порождает некоторые проблемы. В зависимости от контекста, результирующая бесконечность может иметь разную природу и вести себя по-разному. Например, результатом умножения бесконечности положительной бесконечностью может быть положительная бесконечность, но результатом умножения бесконечности отрицательной бесконечностью может быть отрицательная бесконечность.
Также, можно столкнуться с неопределенностями при умножении разных бесконечностей. Например, результатом умножения бесконечности на 0 может быть неопределенность. Это связано с тем, что бесконечность может представлять собой бесконечно большое число, а умножение на 0 означает отсутствие какой-либо величины.
Однако следует помнить, что умножение бесконечностей - это лишь абстрактное понятие, используемое в математике для решения определенных задач и не всегда имеет реальный смысл или применение.
Деление бесконечности
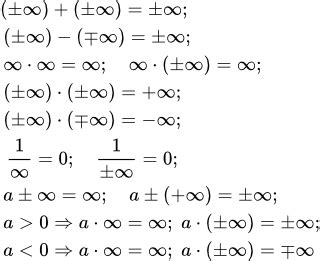
Рассмотрим несколько примеров:
| Пример | Результат |
|---|---|
| ∞ / ∞ | Неопределенность |
| 2∞ / ∞ | Неопределенность |
| ∞ / 2∞ | Неопределенность |
Когда мы делим бесконечность на бесконечность, мы получаем неопределенность. Это связано с тем, что бесконечность не является числом и не подчиняется обычным законам арифметики. В таких случаях требуется более сложный подход к анализу.
Математики часто используют пределы для описания поведения функций или выражений близко к бесконечности. В этом случае результат может быть определен более точно. Однако для простого деления бесконечности на бесконечность множество возможных ответов делает это действие неопределенным.
Когда бесконечность равна бесконечности

Вычитание бесконечности из бесконечности может казаться парадоксальным, но в математике этот процесс имеет свои особенности. Когда мы работаем с бесконечностью, мы сталкиваемся с бесконечно большими числами, и их вычитание может быть неоднозначным.
В некоторых случаях вычитание бесконечности из бесконечности может дать результат, равный бесконечности или бесконечно большому числу. Например, если мы рассмотрим последовательности чисел, которые стремятся к бесконечности и вычитаем одну из другой, результат может быть неопределенным. Это связано с тем, что бесконечность не является конкретным числом и не подчиняется обычным арифметическим правилам.
В отличие от обычной арифметики, в математике существуют концепции, такие как бесконечно малые и бесконечно большие числа. Когда мы говорим о вычитании бесконечности из бесконечности, мы рассматриваем их как пределы последовательностей или функций. В этом контексте, результат может быть определен или сходиться к конкретному значения в зависимости от конкретной задачи или ситуации.
Однако, в обычной арифметике международные стандарты не определяют точный результат вычитания бесконечности из бесконечности. В таких случаях, ответ может быть неопределенным или индетерминированным. Поэтому, при работе с бесконечностью, особенно в контексте математики, необходимо учитывать контекст и точно определять условия и пределы, чтобы получить смысловой результат.
Концепция бесконечно малых чисел

Основная идея бесконечно малых чисел заключается в том, что они позволяют нам анализировать поведение функций и выражений в окрестности заданной точки.
Для более наглядного представления бесконечно малых чисел используется понятие предела. Предел показывает, что происходит с функцией, когда аргумент приближается к определенной точке. Он может быть представлен в виде бесконечно малого числа.
Бесконечно малые числа являются важным инструментом для решения различных задач, включая поиск производных функций, вычисление пределов и разложение функций в ряды Тейлора.
| Примеры бесконечно малых чисел | Представление |
|---|---|
| h стремится к 0 | h → 0 |
| dx стремится к 0 | dx → 0 |
| ε стремится к 0 | ε → 0 |
Благодаря концепции бесконечно малых чисел мы можем анализировать функции и выражения на бесконечно малых и бесконечно больших значениях, а также осуществлять достаточно точные приближения и упрощения вычислений.
Бесконечно большие числа

Понятие бесконечности стремится описать отсутствие границы или конечности. Бесконечно большое число не имеет определенного значения, оно лишь указывает на то, что число превышает все остальные числа. В математической нотации оно может быть обозначено символом ∞ (бесконечность).
Интересно, что когда мы вычитаем или складываем бесконечно большие числа, результат не всегда является определенным. Возможны различные варианты исходов:
- Если из бесконечно большого числа вычесть бесконечно большое число, результат может быть определен, но неизвестен, так как мы не можем точно определить, насколько одно бесконечно большое число больше или меньше другого.
- Если к бесконечно большому числу прибавить бесконечно большое число, результат также может быть неопределенным. Это связано с тем, что бесконечность не подчиняется обычным арифметическим правилам.
- Если из бесконечно большого числа вычесть конечное число, результат будет все равно бесконечно большим. Это связано с тем, что бесконечность неизменна и не может быть ограничена конечным числом.
Бесконечность и бесконечно большие числа являются интересными концепциями в математике, позволяющими рассматривать границы и пределы числовых последовательностей. Они помогают нам лучше понять и объяснить некоторые сложные явления и процессы в мире чисел.
Вычитание бесконечности из бесконечности
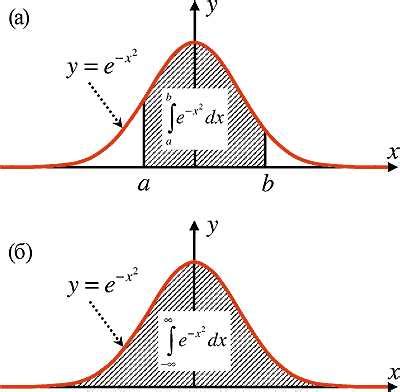
Математически мы можем рассмотреть два примера:
Неопределенность: Если мы вычитаем положительную бесконечность из положительной бесконечности, получится неопределенность вида "бесконечность минус бесконечность". Эта разница не является определенной величиной и может иметь любое значение.
Отрицательная бесконечность: В арифметике с расширенными числами можно рассмотреть случай, когда мы вычитаем положительную бесконечность из отрицательной бесконечности. В этом случае получится отрицательная бесконечность, которая является отдельным концептом и может быть рассмотрена как логическое продолжение бесконечности в отрицательную сторону.
Вычитание бесконечности из бесконечности является одним из примеров, иллюстрирующих сложность работы с бесконечностями и неоднозначность математических операций в бесконечном контексте.
Философские аспекты этой операции

Такая операция становится интересной с философской точки зрения. Она вызывает вопросы о природе бесконечности и о границах математических операций. Один из возможных подходов к пониманию этого явления заключается в использовании теории множеств и абстрактной математики.
Бесконечность может быть рассмотрена как нечто абстрактное, превосходящее наши обычные представления о реальности. В вычислениях она часто используется для приближения к бесконечно большим или малым значениям. Операция вычитания бесконечности из бесконечности позволяет нам исследовать наши представления о математическом понятии равенства и быть более гибкими в нашем понимании этих концепций.
Операция вычитания бесконечности из бесконечности также может быть рассмотрена с философской точки зрения в контексте более общей проблемы конечности и бесконечности. Мы можем рассмотреть ее как попытку описать "ничто" в рамках математической системы, где бесконечность служит своеобразным приближением к этому понятию.
Таким образом, вычитание бесконечности из бесконечности представляет собой сложную и философски значимую проблему, которая требует глубокого понимания искусства математики и философии.



