Произведение синуса на синус – это одно из фундаментальных математических понятий, которое активно используется в различных областях науки. Синус является тригонометрической функцией, которая определяется отношением длины противолежащего катета к гипотенузе в прямоугольном треугольнике. Точное значение синуса может быть найдено с помощью специальных таблиц или с использованием математических формул.
Если у нас есть два угла, для которых известны значения синуса, то можно рассчитать их произведение. Произведение синуса на синус равно половине разности косинусов данных углов. Это выражение можно записать следующим образом: sin(a) * sin(b) = (cos(a - b) - cos(a + b)) / 2.
Произведение синуса на синус имеет важное значение в тригонометрии и используется во множестве математических задач. Оно может быть применено, например, при решении уравнений, моделировании физических процессов или анализе сложных систем. Знание этой формулы позволяет упростить вычисления и найти точные значения искомых величин.
Обзор произведения синуса на синус

Формула для произведения синуса на синус имеет вид:
sin(a) * sin(b) = (cos(a - b) - cos(a + b)) / 2
Здесь a и b - произвольные углы.
Свойства произведения синуса на синус:
- Произведение синусов двух аргументов равно половине разности косинусов этих аргументов.
- Периодичность: значение произведения синуса на синус повторяется через каждый период функции синуса.
- Отношение к аргументам: произведение синуса на синус зависит от разности и суммы аргументов.
Произведение синуса на синус является важным инструментом, используемым при решении уравнений и задач, связанных с колебаниями, периодическими функциями и гармоническими волнами.
Познакомившись с формулой и свойствами произведения синуса на синус, можно более глубоко понять и использовать тригонометрию в различных областях науки и техники.
Определение и основные свойства

Синус - это математическая функция, которая определяется как отношение длины противолежащего катета к гипотенузе в прямоугольном треугольнике.
Операция произведения синуса на синус обозначается следующим образом: sin(a) * sin(b), где a и b - значения углов.
Основные свойства произведения синуса на синус:
- Произведение синуса на синус всегда будет принадлежать интервалу [-1, 1].
- Если один из углов равен нулю, произведение синуса на синус также будет равно нулю.
- Если один из углов равен 90 градусам или \(\frac{\pi}{2}\) радиан, произведение синуса на синус также будет равно нулю.
- Если оба угла равны друг другу, то произведение синуса на синус будет равно квадрату значения синуса данного угла.
Произведение синуса на синус в прямоугольной системе координат
Чтобы разобраться в этой связи, рассмотрим два угла, α и β, и построим соответствующие им точки на плоскости. Угол α будем измерять от оригинальной оси координат, а угол β от оси абсцисс. Тогда координаты точки A с углом α будут (cos α, sin α), а точки B с углом β - (cos β, sin β).
Теперь рассмотрим вектор AB, и найдем его длину. Длина вектора AB равна расстоянию между точками A и B, которое можно вычислить с помощью формулы длины отрезка по координатам:
d = sqrt((cos β - cos α)^2 + (sin β - sin α)^2)
Следующий шаг - преобразовать эту формулу, используя разложение разности синусов и косинусов и замену суммы квадратов на произведение и суммы:
d = sqrt(2 - 2(cos αcos β + sin αsin β))
Выполним замену произведения синуса и косинуса на значение синуса суммы углов по тригонометрической формуле:
d = sqrt(2 - 2sin(α + β))
Таким образом, произведение синуса на синус в прямоугольной системе координат может быть выражено как квадратный корень из разности 2 и 2sin(α + β).
Формула произведения синуса на синус

Произведение синуса на синус равно половине разности косинусов удвоенного аргумента и аргумента:
sin(a) * sin(b) = (cos(2a - b) - cos(b)) / 2
В данной формуле а и b - аргументы синусов.
Эта формула основана на тригонометрическом тождестве: двойной аргумент синуса можно представить через косинусы удвоенного аргумента и самого аргумента.
Произведение синуса на синус в тригонометрических и геометрических задачах
Одним из основных свойств произведения синуса на синус является его периодичность. То есть, если значения углов a и b изменяются на целое число периодов, то значение произведения sin(a)·sin(b) останется неизменным.
Произведение синуса на синус также может быть использовано для решения различных геометрических задач, связанных с треугольниками. Например, для нахождения площади треугольника по двум сторонам треугольника и углу между ними, можно использовать формулу:
| Площадь треугольника | |
|---|---|
| S = 0.5 · a · b · sin(γ) |
Здесь a и b - длины сторон треугольника, а γ - угол между ними.
Также произведение синуса на синус может быть использовано для нахождения высот треугольника или точек пересечения прямых.
Аналитическое вычисление произведения синуса на синус

| Условие | Результат |
|---|---|
| sin(x) * sin(y) | (1/2) * [cos(x - y) - cos(x + y)] |
где x и y - любые углы.
Таким образом, чтобы найти произведение синуса на синус, необходимо вычислить разность и сумму углов, взять косинусы этих значений, а затем вычислить разность этих косинусов. Результатом будет половина этого значения.
Например, если x = 45° и y = 30°:
| x | y | x - y | x + y | cos(x - y) | cos(x + y) | cos(x - y) - cos(x + y) |
|---|---|---|---|---|---|---|
| 45° | 30° | 15° | 75° | 0.966 | 0.259 | 0.966 - 0.259 = 0.707 |
Таким образом, произведение sin(45°) * sin(30°) равно 0.707
Аналитическое вычисление произведения синуса на синус позволяет получить точный результат без использования приближенных значений.
График функции произведения синуса на синус
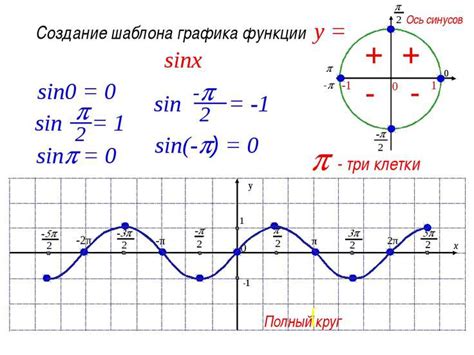
Для построения графика данной функции необходимо просчитать значение функции в нескольких точках на заданном интервале и соединить полученные значения отрезками. Применим метод таблицы для вычисления значений функции.
| x | sin(x) | sin(x) * sin(x) |
|---|---|---|
| 0 | 0 | 0 |
| π/6 | 0.5 | 0.25 |
| π/3 | 0.866 | 0.75 |
| π/2 | 1 | 1 |
| 2π/3 | 0.866 | 0.75 |
| 5π/6 | 0.5 | 0.25 |
| π | 0 | 0 |
Подставив значения аргумента из таблицы в функцию, можно построить график.
График функции произведения синуса на синус представляет собой периодическую кривую, которая проходит через точки максимумов (1) и минимумов (0), а также через нулевой уровень. График симметричен относительно оси ординат.
Связь произведения синуса на синус с другими тригонометрическими функциями

Произведение синуса на синус, обозначаемое как sin(α) × sin(β), может быть выражено следующим образом:
sin(α) × sin(β) = (cos(α - β) - cos(α + β)) / 2
Данная формула позволяет выразить произведение синуса на синус через разность и сумму косинусов, что позволяет упростить и анализировать функции произведения синуса на синус.
Выражение произведения синуса на синус через косинусы является одним из практических применений тригонометрического тождества и может использоваться при решении различных задач и уравнений, связанных с тригонометрией и геометрией.
Также следует отметить, что произведение синуса на синус имеет ряд интересных свойств и особенностей, которые могут быть изучены и использованы при решении задач и построения графиков функций.
Практические применения произведения синуса на синус

Произведение синуса на синус может быть использовано в различных научных и инженерных расчетах, а также в ряде приложений в физике, математике и других дисциплинах. Оно имеет множество практических применений:
| Применение | Описание |
|---|---|
| Оптика | В оптике произведение синуса на синус используется для описания интерференции света. При интерференции волн, производимых двумя источниками, произведение синуса на синус определяет вид интенсивности света в области их перекрытия. |
| Аккустика | В аккустике произведение синуса на синус может использоваться для моделирования звуковых волн и предсказания уровня звукового давления в различных точках пространства. Оно позволяет анализировать резонансные явления и изменение звука при взаимодействии с различными поверхностями. |
| Механика | В механике произведение синуса на синус может использоваться при анализе гармонических колебаний. Например, при моделировании колебаний материального точки на пружине или колебаний маятника произведение синуса на синус определяет зависимость от времени амплитуды колебаний. |
| Электротехника | В электротехнике произведение синуса на синус может использоваться для описания взаимодействия переменных электрических величин, таких как напряжение и ток. Например, в теории электрических цепей произведение синуса на синус может быть использовано для расчета активной и реактивной частей мощности в системе переменного тока. |
Это лишь некоторые примеры практического использования произведения синуса на синус. Знание и понимание его свойств позволяет решать разнообразные задачи в различных научных и инженерных областях.



