Квадрат модуля - одна из основных операций в математике, которая интересует многих учеников и студентов. Эта операция позволяет нам получить четыре очень важные величины: положительное число, отрицательное число, ноль и единицу. Каждая из этих величин имеет свои особенности и может быть использована для решения различных задач и проблем.
Когда мы берем квадрат модуля числа, мы возводим это число в квадрат и затем берем модуль полученного результата. Если изначально у нас было положительное число, то после возведения его в квадрат оно останется положительным. Если же изначально у нас было отрицательное число, то после возведения его в квадрат оно станет положительным. Ноль же при возведении в квадрат останется нулем. И только единица при возведении в квадрат останется единицей.
Квадрат модуля может быть использован в различных областях математики, физики и информатики. Например, он может быть применен для решения задач, связанных с определением расстояния между точками на координатной плоскости, определением изменения состояния физической системы или анализа данных при работе с программами и алгоритмами. Изучение этой операции позволяет нам получить более глубокое понимание мира, в котором мы живем, и улучшить наши математические навыки и умения.
Влияние взятия квадрата модуля
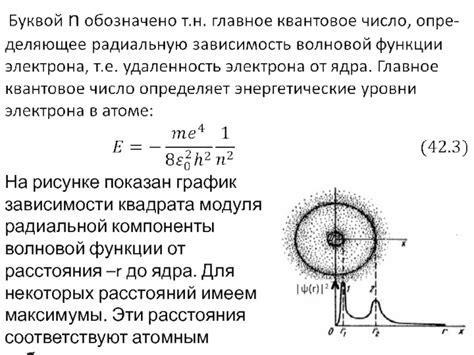
Взятие квадрата модуля числа играет важную роль в различных областях математики и физики. Эта операция позволяет получить положительное значение числа, независимо от его знака.
Применение операции взятия квадрата модуля имеет ряд важных свойств:
1. Устранение знака: Взятие квадрата модуля числа позволяет устранить знак. Это позволяет использовать полученное значение для описания только величины числа, независимо от его положительности или отрицательности.
2. Получение положительного значения: Квадрат модуля всегда дает положительное число. Это позволяет работать с абсолютными величинами чисел и использовать их в различных вычислениях и анализах.
3. Приложение в физике и статистике: Взятие квадрата модуля широко применяется в физике и статистике. Например, в физике это может быть использовано для описания кинетической энергии частицы или для описания интенсивности сигнала в определенном точке пространства. В статистике квадрат модуля может использоваться для вычисления дисперсии и вариации величин.
4. Упрощение математических выражений: Взятие квадрата модуля часто позволяет упростить математические выражения. Это может быть полезно при решении уравнений, проведении анализа функций и выполнении других операций.
Таким образом, взятие квадрата модуля имеет значительное влияние на различные области математики и физики. Эта операция позволяет удобно работать с числами, устраняя их знак и получая положительные значения, что облегчает анализ и вычисления.
Изменение значения числа
Когда мы возведем число в квадрат и возьмем его модуль, происходит изменение его значения.
Возведение числа в квадрат означает, что мы умножаем число на себя самого. Результат этой операции всегда будет положительным числом. Ноль возводится в квадрат также как и любое другое число, а именно - умножением на себя.
Взятие модуля числа означает, что мы отбрасываем его знак и оставляем только абсолютную величину. Если число положительное или равно нулю, его модуль не меняется. Если число отрицательное, его модуль становится положительным.
Итак, когда мы берем квадрат модуля числа, мы умножаем число на себя самого и затем отбрасываем его знак. Таким образом, мы всегда получаем неотрицательное значение числа.
Изменение значения числа при взятии его квадрата и модуля может быть полезным во многих контекстах, например, при работе с алгеброй, геометрией или в программировании.
Изменение знака числа

При взятии квадрата модуля числа происходит изменение его знака. Если исходное число было положительным, то после взятия квадрата модуля оно останется положительным. Если же исходное число было отрицательным, то после взятия квадрата модуля оно станет положительным.
Например, если исходное число равно -5, то его квадрат модуля будет равен 25, что является положительным числом.
Взятие квадрата модуля часто используется в математике для получения положительного значения величины без учета ее знака. Это может быть полезно при решении различных задач, а также при работе с комплексными числами.
| Исходное число | Квадрат модуля |
|---|---|
| 3 | 9 |
| -7 | 49 |
| 0 | 0 |
Возможность применения в математических операциях

Если даны две точки A(x1, y1) и B(x2, y2), то расстояние между ними можно найти с помощью формулы:
d = √((x2 - x1)2 + (y2 - y1)2)
В этой формуле вычисляется квадрат модуля числа в каждом из скобок, что позволяет получить положительное значение и избежать проблем с отрицательными числами.
Кроме того, квадрат модуля числа применяется в задачах оптимизации и минимизации функций. Вычисление квадрата модуля позволяет убрать знак числа, что может быть полезно при поиске экстремумов функций.
Также, квадрат модуля числа используется в задачах статистики и вероятности. Например, в формуле для вычисления дисперсии случайной величины X:
D(X) = E((X - E(X))2)
где E(X) - математическое ожидание случайной величины X. Вычисление квадрата модуля числа позволяет получить положительное значение, не зависящее от знака разности (X - E(X)).
Таким образом, квадрат модуля числа имеет широкую область применения в математических операциях, с которыми мы встречаемся в различных научных и инженерных областях.
Связь с комплексными числами

В математике комплексные числа представляются двумерными векторами на плоскости, где каждому числу сопоставляется точка. Это позволяет работать с более широким спектром числовых значений и решать разнообразные задачи.
Квадрат модуля комплексного числа позволяет нам получить величину, называемую аргументом. Аргумент - это угол между положительным направлением оси x и лучом, проведенным от начала координат до точки, соответствующей комплексному числу.
Квадрат модуля комплексного числа является суммой квадратов его действительной и мнимой частей. Таким образом, он представляет собой меру его "размера" или "длины". Используя эту информацию, мы можем сравнивать и строить операции над комплексными числами.
Взятие квадрата модуля комплексного числа иногда используется для упрощения вычислений или анализа различных задач, например, при решении уравнений в комплексных числах, поиске корней или определении свойств кривых.
Таким образом, взятие квадрата модуля комплексного числа является важной операцией, которая позволяет нам получить дополнительную информацию о числе и использовать ее для решения различных задач в математике и других науках.
Применение в физических задачах

В физике квадрат модуля часто применяется для получения положительных значений физических величин, которые могут быть как положительными, так и отрицательными.
Одна из таких физических задач, где применяется квадрат модуля, - это определение кинетической энергии. Кинетическая энергия тела определяется как половина произведения массы тела на квадрат его скорости. Поскольку скорость может быть как положительной, так и отрицательной величиной, то квадрат модуля скорости гарантирует получение положительного значения кинетической энергии.
Другим примером применения квадрата модуля в физических задачах является закон всемирного тяготения, который описывает силу притяжения между двумя телами. Формула этого закона представляет собой произведение масс двух тел, разделенное на квадрат расстояния между ними. Квадрат модуля расстояния гарантирует получение положительного значения для силы притяжения вне зависимости от направления расстояния между телами.
Также, в физике, квадрат модуля может применяться для определения мощности в цепи переменного тока. Мощность в этом случае равна произведению квадрата тока на сопротивление цепи. Квадрат модуля тока учитывает, что его значение может меняться отрицательно на положительное во время периода.
Все эти примеры показывают, что применение квадрата модуля в физических задачах позволяет строго работать с положительными величинами и обеспечивает правильные результаты расчетов.
Влияние на графики функций
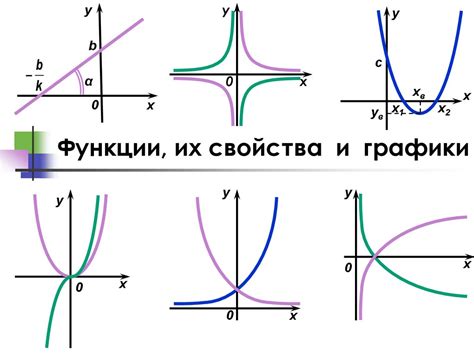
Взятие квадрата модуля функции может привести к значительным изменениям в ее графике. В основном, это связано с тем, что квадрат модуля всегда дает неотрицательное значение, а также с усилением "выпуклости" или "вогнутости" графика.
Квадрат модуля функции представляет собой процесс, при котором каждое значение функции возводится в квадрат, а затем берется модуль полученного результата. Это можно записать как |f(x)|^2.
Одним из основных эффектов взятия квадрата модуля является превращение всех отрицательных значений функции в положительные. Это происходит потому, что в квадрате все числа становятся положительными. Таким образом, все точки, которые находятся ниже оси OX на графике исходной функции, после взятия квадрата модуля поднимутся выше оси OX.
Еще одним важным эффектом является изменение выпуклости графика функции. Если исходный график был выпуклым вниз (вогнутым), то после взятия квадрата модуля он станет выпуклым вверх. Это происходит потому, что в квадрате все отрицательные значения возведутся в положительную степень, что приведет к повороту графика вверх. В случае, если исходный график был выпуклым вверх, то после взятия квадрата модуля он останется выпуклым вверх.
Таким образом, взятие квадрата модуля функции существенно влияет на ее график, превращая все отрицательные значения в положительные и изменяя выпуклость графика. Это важно учитывать при анализе и использовании функциональных зависимостей в различных областях науки, инженерии и экономике.
Роль в теории вероятностей

Квадрат модуля представляет собой операцию возведения случайной величины в квадрат и получения абсолютного значения. Это действие позволяет убрать отрицательные значения и сконцентрироваться только на положительных значениях случайной величины.
Одним из важных применений квадрата модуля является вычисление вероятностей. Вероятность определенного события может быть выражена через квадрат модуля случайной величины и некоторой функции плотности вероятности.
Например, при решении задач по сочетанию событий или применении теоремы Байеса, квадрат модуля может быть использован для вычисления вероятностей событий с использованием теории векторов.
Квадрат модуля также активно используется при изучении случайных процессов и статистических моделей. Он позволяет проводить анализ дискретных временных рядов, стохастической динамики и многих других статистических процессов.
Практическое применение в программировании

В программировании квадрат модуля часто используется в различных математических и физических расчетах. Например, квадрат модуля может быть полезен при решении задач, связанных с вычислением расстояния между двумя точками в пространстве.
Если у нас есть две точки с координатами (x1, y1) и (x2, y2), то расстояние между ними можно вычислить по формуле:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
Однако, если нам не требуется точное значение расстояния, а достаточно сравнивать расстояния между несколькими точками, то можем воспользоваться квадратом модуля. Вместо вычисления корня, мы можем взять квадрат суммы квадратов разностей в координатах:
d^2 = (x2 - x1)^2 + (y2 - y1)^2
Такой подход позволяет избежать извлечения квадратного корня и сэкономить ресурсы компьютера. Особенно это актуально при работе с большими наборами данных или при выполнении вычислений в режиме реального времени.
Квадрат модуля также может быть полезен при проверке и сравнении значений. Например, при сравнении двух величин, мы можем сравнить их квадраты без необходимости взятия модуля и обеспечить более эффективное выполнение программы.
Использование квадрата модуля в программировании приводит к оптимизации вычислений и повышению производительности программ и алгоритмов.



