Геометрия – это наука, которая изучает пространственные фигуры и их свойства. В основе геометрии лежат два основных понятия: точка и прямая. Точка – это одномерный объект, не имеющий ни длины, ни ширины, ни толщины. Прямая – это бесконечное множество точек, расположенных в одной линии. Эти два понятия являются основными строительными блоками геометрии и на их основе формируются все остальные объекты и понятия.
Точка в геометрии обозначается заглавной латинской буквой. Например, A, B, C. Точки могут иметь различные свойства, такие как координаты, цвет, название и другие. В геометрии точка используется для задания местоположения других объектов, таких как прямые, отрезки, углы и многие другие. Точка также может быть точкой пересечения нескольких прямых или других фигур.
Прямая – это бесконечно протяженный объект, который не имеет начала и конца. Прямая обозначается двумя точками, расположенными на ней. Например, AB. Прямая может иметь различные свойства, такие как длина, углы, параллельность и другие. В геометрии прямая используется для соединения двух точек или для разделения плоскости на две части. Прямая может быть горизонтальной, вертикальной или наклонной.
В данной статье мы рассмотрим подробно понятия точки и прямой, их свойства и взаимосвязь. Мы также приведем примеры и задачи, чтобы лучше разобраться в этих понятиях и их применении в геометрии. Понимание и владение этими основными понятиями поможет вам лучше понять и решать геометрические задачи и проблемы, а также применять геометрию в различных сферах жизни.
Что такое точка в геометрии и как ее определить?
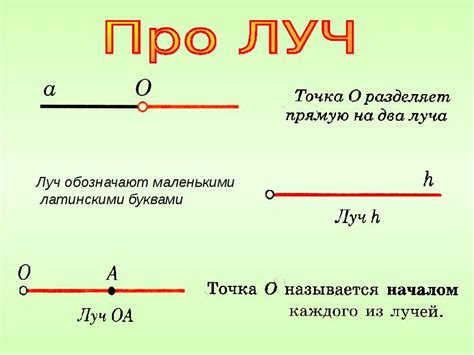
Точку в геометрии можно определить как место пересечения двух прямых или как точку на поверхности, на которой может находиться объект. В геометрии точки также используются для задания координат на плоскости или в пространстве.
Например, в двумерной геометрии точка может быть задана парой координат (x, y), где x - это горизонтальная координата, а y - вертикальная координата. В трехмерной геометрии точка может быть задана тройкой координат (x, y, z).
Точка является основным понятием в геометрии, и она используется для определения всех других геометрических фигур, таких как линия, плоскость или тело. Без точек геометрия не существовала бы, так как все геометрические фигуры состоят из точек.
Основные свойства и характеристики точки в геометрии

Основные характеристики точки в геометрии включают:
- Координаты точки: для удобства работы с точками на плоскости или в пространстве могут быть введены координатные системы. Так, в декартовой системе координат каждая точка представляется упорядоченной парой чисел (x, y) на плоскости и тройкой чисел (x, y, z) в пространстве. Координаты определяют положение точки относительно начала координат и позволяют вычислять расстояния между точками, углы и т. д.
- Расстояние между точками: можно определить как длину отрезка прямой, соединяющей две точки. Расстояние между точками можно вычислить с использованием координат точек и формулы расстояния.
- Симметрия: точка может быть отражена относительно прямой, оси или другой точки. Такие преобразования называются симметриями и являются важным аспектом геометрии точки.
- Принадлежность фигурам: точка может принадлежать геометрическим фигурам, таким как прямые, плоскости, окружности и многоугольники. Точки, лежащие на одной линии, называются коллинеарными точками, а точки, лежащие на одной плоскости, называются соколлинеарными точками.
Основные свойства и характеристики точки в геометрии позволяют проводить различные операции и преобразования, а также анализировать геометрические объекты и их взаимодействия.
Что такое прямая и как ее определить?
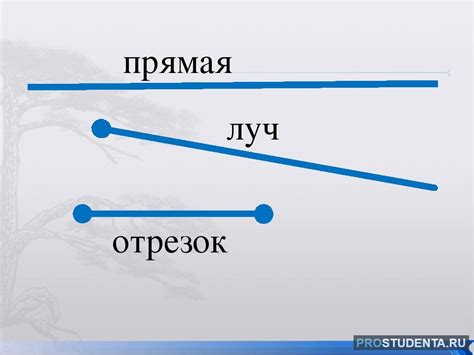
- Прямая не имеет начала и конца, она обладает бесконечной протяженностью.
- На прямой любые две ее точки можно соединить отрезком, который полностью лежит на этой прямой.
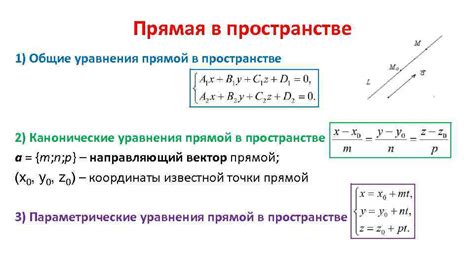
Прямая может быть представлена различными способами. Один из самых распространенных способов - это задание прямой с помощью уравнения. В математике, прямую можно определить с помощью уравнения вида:
ax + by + c = 0
где a, b и c - это коэффициенты, которые определяют положение прямой в пространстве. Зная значения этих коэффициентов, можно определить угол наклона прямой и пересечение с осями координат.
Кроме того, прямые могут быть определены с помощью геометрических построений. Например, прямая может быть определена как геометрическое место точек, равноудаленных от двух заданных точек. Или как геометрическое место точек, которые лежат на одной прямой с заданной точкой и заданным наклоном.
Использование прямых в геометрии широко распространено. Они используются для построения геометрических фигур, решения уравнений, изучения свойств пространства и многое другое. Понимание понятия прямой в геометрии является важным шагом для изучения более сложных концепций и теорий в этой области.
Примеры использования прямой в геометрии
Вот несколько примеров использования прямой в геометрии:
Соединение двух точек: Прямая может использоваться для соединения двух точек на плоскости. Например, чтобы соединить две точки A и B, мы можем провести прямую через них.
Определение отрезка: Прямая может быть использована для определения отрезка - части прямой, которая имеет конечные точки. Отрезок можно представить как участок прямой, ограниченный двумя точками.
Построение углов: Прямая может быть использована для построения различных типов углов. Например, прямая может быть базовой линией при построении прямого угла, острого угла или тупого угла.
Решение задач на координатной плоскости: Прямая может быть задана уравнением на координатной плоскости и использоваться для решения различных геометрических задач. Например, прямая может использоваться для нахождения точек пересечения двух прямых или для построения графика функции.
Аппроксимация кривой: В некоторых случаях, прямая может использоваться для аппроксимации кривой. Например, можно использовать ломаную прямую, состоящую из множества коротких прямых сегментов, чтобы приблизить сложную кривую фигуру.
Это лишь некоторые примеры использования прямой в геометрии. Прямая является одной из основных концепций геометрии и играет важную роль в анализе и решении разнообразных задач.



