Колебания – это повторяющееся изменение какой-либо величины с течением времени. Они встречаются повсеместно в живой и неживой природе: от постоянно колеблющихся атомов и молекул до колебаний звуковой волны и сигнала в электрической цепи. Колебания имеют свои особенности и строение, которые изучаются в физике.
Гармонические колебания – это один из типов колебаний, при которых величина, находящаяся в колеблющемся состоянии, изменяется синусоидально по закону гармонической функции. Гармонические колебания наиболее распространены в природе и широко применяются в научных и технических расчетах, например, в теории звука, синусоидальных электрических сигналов и т. д.
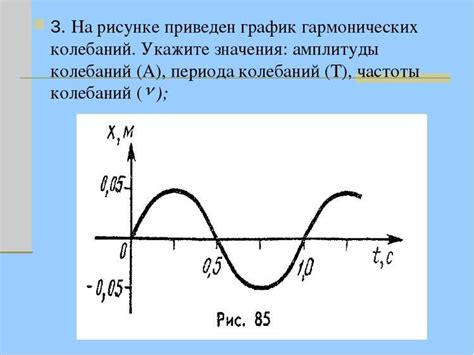
В гармонических колебаниях выделяются такие понятия, как амплитуда, период, частота и фаза. Амплитуда - это наибольшее отклонение от равновесного положения, а период - временной интервал, за который происходит один полный цикл колебаний. Частота - это обратная величина периода и измеряется в герцах (Гц), а фаза - это смещение колеблющейся величины относительно начального положения.
Определение колебаний и гармонических колебаний
Колебания представляют собой повторяющиеся изменения величины или состояния объекта или системы. Это явление широко распространено в природе и технике, и охватывает множество различных явлений, от колебаний звука и света до колебаний в электрических цепях и движении планет.
Гармонические колебания - это особый тип колебаний, при которых величина колеблющегося объекта или системы изменяется с течением времени в соответствии с гармонической функцией. Гармоническая функция представляет собой синусоидальную зависимость, в которой величина меняется с постоянной частотой и амплитудой. Эти колебания являются основой для описания многих явлений в физике и математике.
Основными характеристиками гармонических колебаний являются амплитуда, период и частота. Амплитуда представляет собой максимальное отклонение величины от ее равновесного положения. Период - это время, за которое колеблющийся объект или система проходит один полный цикл колебаний. Частота - это количество полных циклов колебания, проходящих через точку за единицу времени.
Гармонические колебания также могут быть описаны с помощью уравнений движения, которые связывают величину колеблющегося объекта или системы с временем. Например, для гармонического осциллятора уравнение движения может быть представлено формулой Гарриота или уравнением Гармоника. Эти уравнения позволяют предсказывать поведение колеблющихся объектов и систем в различных условиях.
Гармонические колебания имеют важное значение в науке и технике, а также в повседневной жизни. Они используются в широком спектре приложений, включая измерение времени с помощью механических и электронных часов, передачу звука и сигналов в области телекоммуникаций, изучение свойств материалов и процессов в физике и магнитной резонансной томографии, а также в музыке и искусстве.
Колебания - движение вокруг равновесного положения

Колебания представляют собой основную форму движения, которая присутствует во многих физических системах. Они возникают, когда система отклоняется от равновесия и начинает двигаться вокруг этого положения. Данное движение может быть регулярным и повторяющимся, что приводит к образованию гармонических колебаний.
Гармонические колебания являются особым случаем колебательного движения. Они характеризуются тем, что возвращающая сила, действующая на систему, пропорциональна отклонению от положения равновесия и всегда направлена противоположно этому отклонению. Таким образом, система движется взад-вперед вокруг равновесного положения.
Гармонические колебания имеют свои основные параметры, такие как амплитуда, период, частота и фаза. Амплитуда представляет собой максимальное отклонение системы от положения равновесия. Период - это время, за которое система выполняет одно полное колебание. Частота равна обратному периоду и показывает, сколько колебаний выполняет система в единицу времени. Фаза характеризует относительное положение системы в момент времени относительно начального положения.
Гармонические колебания широко применяются в различных областях физики, таких как механика, электродинамика, акустика и оптика. Они играют важную роль в объяснении множества природных явлений, а также в разработке и создании различных устройств и систем.
| Параметр | Описание |
|---|---|
| Амплитуда | Максимальное отклонение системы от положения равновесия. |
| Период | Время, за которое система выполняет одно полное колебание. |
| Частота | Количество колебаний системы в единицу времени. |
| Фаза | Относительное положение системы в момент времени относительно начального положения. |
Гармонические колебания - особый вид колебаний
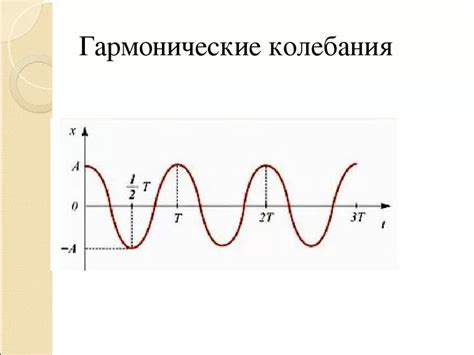
Гармонические колебания представляют собой один из основных видов механических колебаний. Они характеризуются тем, что их амплитуда и частота остаются постоянными в течение всего процесса колебаний.
Основным параметром гармонических колебаний является амплитуда, которая представляет собой максимальное отклонение колеблющейся системы от положения равновесия. Амплитуда напрямую связана с энергией системы и определяет величину колебаний.
Частота гармонических колебаний определяет количество колебаний, выполняемых за единицу времени. Она измеряется в герцах (Гц) и является обратной величиной к периоду колебаний. Чем выше частота колебаний, тем быстрее система совершает колебания.
Гармонические колебания можно представить в виде синусоидальной функции. Отклонения колеблющейся системы от положения равновесия могут быть положительными и отрицательными, что отражается на форме графика.
Гармонические колебания имеют множество практических применений, в том числе в области физики, электроники, механики и музыки. Они играют важную роль в исследовании свойств материалов, создании электрических цепей, работы механических устройств и создании музыкальных звуков.
Характеристики колебаний и гармонических колебаний
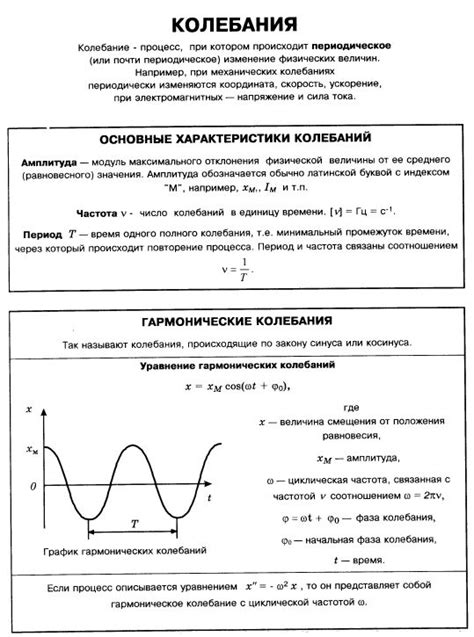
Колебания представляют собой повторяющиеся изменения физической величины вокруг некоторого равновесного состояния. Они возникают в различных системах, включая механические, электрические и акустические.
Одна из основных характеристик колебаний - амплитуда. Амплитуда колебаний определяет максимальное значение изменения физической величины во время одного полного цикла колебаний. Чем больше амплитуда, тем сильнее колебания.
Другой важной характеристикой является период колебаний. Период колебаний обозначает время, за которое физическая величина проходит один полный цикл колебаний. Он измеряется в секундах и обозначается символом T. Чем меньше период колебаний, тем выше частота колебаний.
Частота колебаний - это количество полных циклов колебаний, происходящих за единицу времени. Она обратно пропорциональна периоду колебаний и обозначается символом f. Частота измеряется в герцах (Гц) и выражается формулой f = 1/T.
Гармонические колебания - это особый вид колебаний, в которых физическая величина меняется по гармоническому закону. Они характеризуются постоянной частотой и амплитудой. Такие колебания широко встречаются в природе и технике, например, в звуковых волнах и электрических сигналах.
Гармонические колебания могут быть описаны с помощью тригонометрической функции синуса или косинуса. Эта функция позволяет определить изменение физической величины в зависимости от времени. Фаза колебаний определяет начальное положение колеблющейся системы и может быть выражена с помощью угла в радианах или градусах.
Амплитуда - максимальное отклонение от равновесного положения
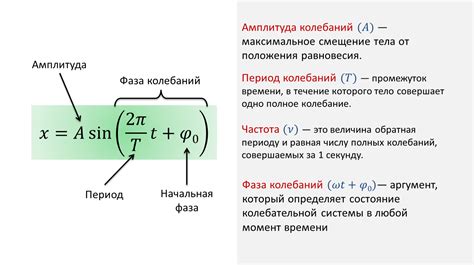
Амплитуда играет важную роль в описании колебаний, так как она определяет крутизну графика, характеризующего движение объекта. Чем больше амплитуда, тем больше энергии требуется для движения объекта и тем сильнее колебания.
Амплитуда может измеряться в различных единицах, в зависимости от конкретной системы. Например, для колебаний массы на пружине, амплитуда может измеряться в метрах или сантиметрах. Для электромагнитных колебаний, амплитуда измеряется в вольтах.
Знание амплитуды позволяет предсказывать свойства и характеристики колебаний, такие как период, частота и фазовая разность. С помощью амплитуды можно также оценить максимальную скорость и ускорение, которые достигаются во время колебаний.
Важно отметить, что амплитуда является свойством самого колеблющегося объекта и не зависит от внешних факторов, таких как сила, вызывающая колебания. Поэтому изменение амплитуды может быть результатом воздействия внешних сил или нарушения условий колебаний.



