Ось симметрии треугольника – это воображаемая линия, которая разделяет его на две равные части, симметричные относительно этой линии. Одна часть треугольника зеркально отображает другую вдоль оси симметрии. Понимание оси симметрии треугольника является важным в 3 классе, поскольку это базовый концепт симметрии, который впоследствии будет применяться в изучении более сложных геометрических фигур.
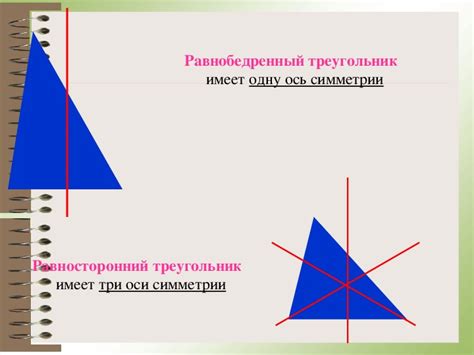
В треугольнике может быть одна, две или три оси симметрии. Если у треугольника есть только одна ось симметрии, то он считается симметричным. Если это треугольник равнобедренный, то у него всегда есть одна ось симметрии – медиана, которая проходит через вершину и середину основания треугольника. Если треугольник равносторонний, у него будет не только одна, но и две оси симметрии – медиана, проходящая через вершину и середину основания, и медиатриса, которая перпендикулярна биссектрисе.
Для треугольников с различными сторонами и углами может быть три оси симметрии – медиана и две медиатрисы. Медиана проходит через вершину треугольника и середину противоположной стороны. Медиатриса – это линия, перпендикулярная противоположной стороне и проходящая через середину этой стороны.
Что такое ось симметрии треугольника в 3 классе
В третьем классе дети изучают основные понятия симметрии, включая ось симметрии фигур. Ось симметрии является важным понятием не только в математике, но и в реальной жизни. Она используется, например, при создании зеркал, мебели или других предметов, которые имеют симметричную форму.
Чтобы найти ось симметрии треугольника, нужно просто нарисовать линию, которая будет делить треугольник на две равные части. Если вы сможете свернуть одну половинку треугольника по этой линии, она точно совпадет с другой половинкой.
Ось симметрии может быть горизонтальной, вертикальной или диагональной, в зависимости от формы треугольника. Например, равнобедренный треугольник имеет ось симметрии по биссектрисе одного из углов. Прямоугольный треугольник может иметь ось симметрии, проходящую через его гипотенузу.
Знание оси симметрии помогает детям в развитии пространственного воображения и понимании геометрических форм. Это важное понятие, которое используется не только в математике, но и в других науках и практических областях.
Структура треугольника и его особенности
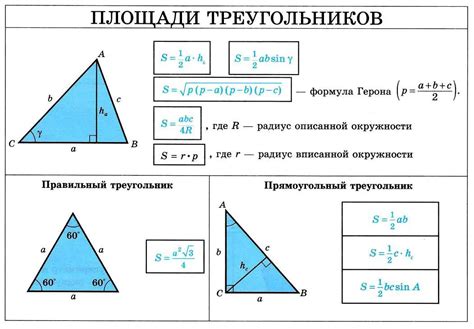
Три стороны треугольника могут иметь разные длины, что делает треугольник разносторонним. Если все три стороны треугольника имеют одинаковую длину, то треугольник называется равносторонним. Равнобедренный треугольник имеет две равные стороны.
Треугольник также имеет три угла. Сумма всех углов треугольника всегда равна 180 градусам. В треугольнике может быть прямой угол, когда один из углов равен 90 градусам, или острый угол, когда все углы меньше 90 градусов. Если один из углов больше 90 градусов, то треугольник называется тупоугольным.
Ось симметрии треугольника - это вымышленная линия, которая делит треугольник на две симметричные половины. Она проходит через середину стороны треугольника и перпендикулярна к этой стороне. Если треугольник прямоугольный, то осью симметрии будет являться его гипотенуза.
| Тип треугольника | Описание |
|---|---|
| Равносторонний треугольник | Все стороны равны |
| Равнобедренный треугольник | Две стороны равны |
| Прямоугольный треугольник | Имеет один прямой угол (90 градусов) |
| Остроугольный треугольник | Все углы меньше 90 градусов |
| Тупоугольный треугольник | Один из углов больше 90 градусов |
Знание основных характеристик треугольников позволяет более глубоко изучать геометрию и использовать их в различных математических задачах.
Ось симметрии и ее определение
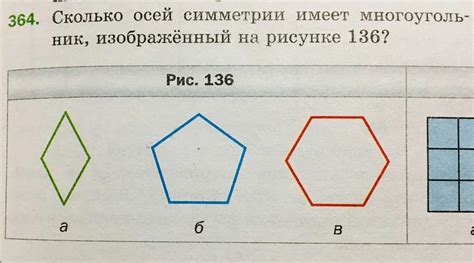
У треугольника может быть одна или несколько осей симметрии. Если ось симметрии проходит через вершину треугольника и середину противоположной стороны, то такая ось называется осью симметрии треугольника. Если ось симметрии проходит через середину одной стороны и середину противоположной стороны, то треугольник не имеет оси симметрии.
Ось симметрии - это характеристика фигуры, которая, помимо треугольника, может быть также применима для других геометрических фигур, таких как квадрат, круг, прямоугольник и т.д. Знание оси симметрии поможет определить, насколько симметричной является фигура или какая из ее частей симметричная.
Как найти ось симметрии треугольника
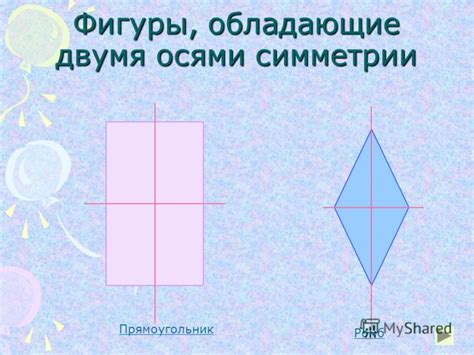
- Находите середины сторон треугольника: для этого соедините конец одной стороны с серединой противоположной стороны.
- Получите на плоскости точки пересечения полученных в предыдущем шаге отрезков.
- Найдите середину отрезка, соединяющего вершину треугольника с полученной точкой.
- Проведите прямую, проходящую через вершину треугольника и найденную середину отрезка. Эта прямая будет осью симметрии треугольника.
Также стоит отметить, что треугольник может иметь более чем одну ось симметрии, если он равносторонний или прямоугольный.
Примеры оси симметрии треугольника
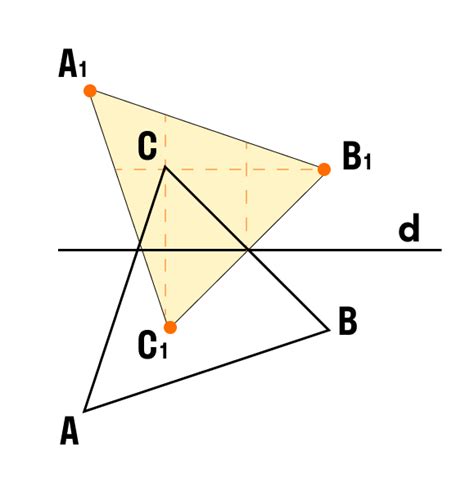
- В равностороннем треугольнике каждая высота, медиана и биссектриса являются осями симметрии.
- В равнобедренном треугольнике осью симметрии является медиана, проведенная из вершины, лежащей против основания.
- В прямоугольном треугольнике осью симметрии является биссектриса, проведенная из прямого угла к гипотенузе.
- В произвольном треугольнике может быть несколько осей симметрии, если треугольник имеет определенные свойства, например, симметрию относительно вершин или срединных перпендикуляров.
Оси симметрии позволяют нам определить сходство или симметрию различных геометрических фигур, их свойства и взаимные положения. Изучение осей симметрии в треугольниках помогает нам лучше понять их геометрические свойства и использовать их в разных дисциплинах, таких как геометрическая алгебра и анализ формы.
Роль оси симметрии в геометрии
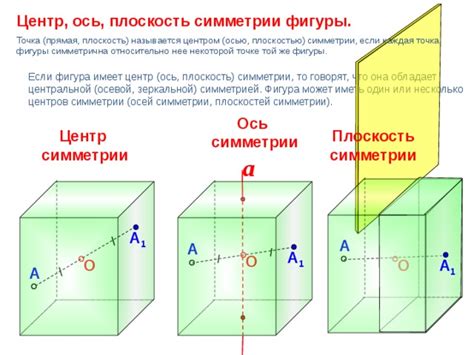
Ось симметрии – это линия, которая делит фигуру на две симметричные части. В геометрии ось симметрии играет важную роль и помогает нам находить сходство и правильность в различных фигурах.
Основные свойства оси симметрии:
1. Равенство частей: При наличии оси симметрии каждая часть фигуры будет точно соответствовать другой. Это значит, что если мы возьмем одну часть фигуры и разместим ее вдоль оси симметрии, то она полностью совпадет с другой частью.
2. Сохранение углов и длин: Ось симметрии сохраняет углы и длины фигуры. Например, если угол в фигуре равен 90 градусов, то его отображение через ось симметрии также будет иметь угол в 90 градусов.
3. Регулярные фигуры: Ось симметрии имеют регулярные фигуры, такие как треугольник, прямоугольник и круг. В регулярном треугольнике оси симметрии проходят через все три стороны и центр окружности.
Ось симметрии используется в геометрии для определения и классификации фигур. Она помогает нам понять, какие части фигуры являются симметричными и какие трансформации можно применить для создания симметричной фигуры.
Ось симметрии и ее применение в повседневной жизни
Ось симметрии треугольника - это линия, которая делит треугольник на две равные части, которые отражают друг друга.
Понимание оси симметрии треугольника имеет практическое применение в повседневной жизни. Она помогает нам создавать симметричные и красивые фигуры и предметы. Например, когда мы рисуем или вырезаем орнаменты, зеркала или окна в доме, мы часто используем ось симметрии, чтобы сделать фигуру более симметричной и привлекательной.
Также ось симметрии треугольника может помочь нам определить, является ли фигура равносторонним треугольником. Если треугольник имеет три равные стороны и три оси симметрии, то он является равносторонним треугольником.
Изучение оси симметрии треугольника помогает нам развивать свое чувство пропорции, внимательность и геометрическое мышление. Эти навыки пригодятся нам не только при работе с геометрическими фигурами, но и в повседневной жизни, например, при подгонке предметов или украшении.
Поэтому важно понимать, что такое ось симметрии треугольника и как ее применять в повседневной жизни, чтобы создавать симметричные, красивые и привлекательные фигуры и предметы.



