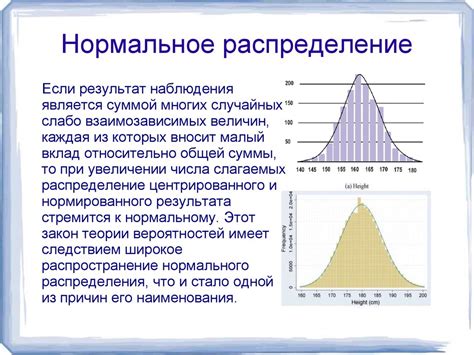
Нормальный закон распределения или нормальное распределение является одним из наиболее распространенных и важных законов вероятности и статистики. Нормальное распределение характеризуется симметричной формой графика и является главным представителем семейства непрерывных распределений. Оно широко используется в различных областях, таких как физика, экономика, социология и биология.
Нормальное распределение задается двумя параметрами: средним значением (математическим ожиданием) и стандартным отклонением. Среднее значение определяет центральную точку распределения, а стандартное отклонение показывает, насколько значения случайной величины отклоняются от среднего значения. Нормальное распределение имеет форму колокола и симметрично относительно среднего значения.
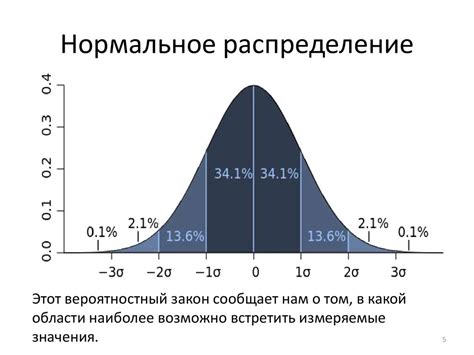
Особенностью нормального распределения является правило трех сигм (правило 68-95-99.7): около 68% значений случайной величины находятся в пределах одного стандартного отклонения от среднего, около 95% значений - в пределах двух стандартных отклонений, и примерно 99,7% - в пределах трех стандартных отклонений. Это правило дает представление о том, как распределены значения случайной величины относительно среднего значения.
Нормальное распределение имеет много применений в статистике, так как многие случайные величины, такие как рост, вес, IQ и результаты экзаменов, подчиняются нормальному закону распределения. Оно также позволяет проводить различные статистические тесты и оценивать вероятность получения определенных значений. Поэтому нормальное распределение играет важную роль в анализе данных и принятии решений на основе статистических данных.
Определение нормального закона распределения
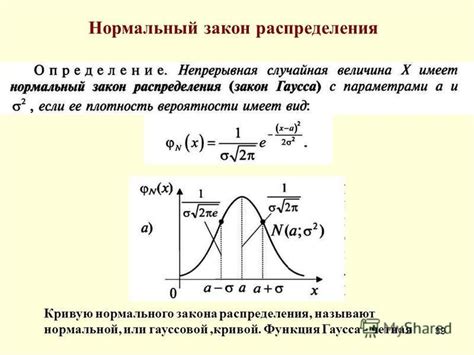
Нормальное распределение характеризуется симметричной колоколообразной формой графика. Оно имеет пик в центре и распределено равномерно в обоих направлениях. Случайная величина в данном распределении имеет бесконечное количество значений.
Нормальное распределение определяется двумя параметрами: математическим ожиданием (μ) и среднеквадратическим отклонением (σ). Математическое ожидание представляет собой среднее значение распределения, а среднеквадратическое отклонение показывает разброс значений относительно среднего.
Множество случайных переменных в реальной жизни приближается нормальным распределением. Например, рост людей, вес и IQ-показатель. Нормальное распределение удобно использовать для анализа и предсказания значений случайных величин.
Особенности нормального закона распределения:
1. Симметрия: Кривая нормального распределения симметрична относительно вертикальной оси, проходящей через математическое ожидание.
2. Выгиб: Кривая нормального распределения имеет пик в районе математического ожидания и выгибается в обе стороны.
3. Ограничение: Нормальное распределение имеет асимптотический характер, что означает, что кривая никогда не касается оси X.
Нормальное распределение является основой для многих статистических тестов и моделей. Оно позволяет исследователям анализировать и интерпретировать данные с помощью математических методов. Нормальное распределение также служит основой для построения других распределений и моделей.
Математическая формула нормального распределения
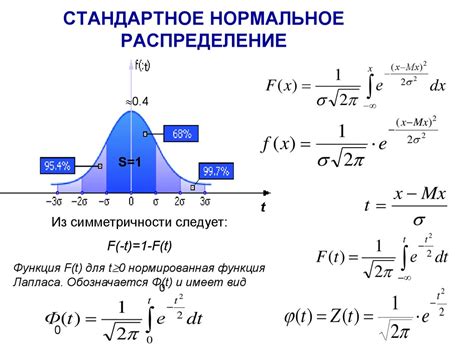
Математическая формула нормального распределения выглядит следующим образом:
P(x) = (1 / σ√(2π)) * e^(-((x-μ)^2 / (2σ^2)))
где:
- P(x) – вероятность плотности распределения случайной величины x;
- μ – математическое ожидание (среднее) распределения;
- σ – стандартное отклонение (разброс) распределения;
- e – основание натурального логарифма (≈ 2.71828).
Эта формула позволяет определить вероятность попадания значения случайной величины x в интервал. График нормального распределения имеет форму колокола, симметричного относительно математического ожидания и ограниченного по вертикали максимальным значением вероятности плотности.
Знание математической формулы нормального распределения позволяет проводить статистические анализы, оценивать вероятности событий и получать информацию о свойствах случайной величины.
Основные характеристики нормального закона распределения
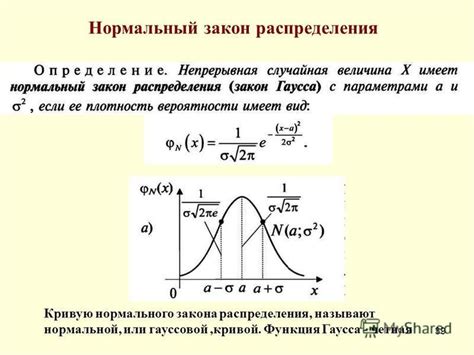
- Симметрия: Нормальное распределение симметрично относительно своего среднего значения. Это означает, что вероятность значений, находящихся слева и справа от среднего значения, одинакова.
- Одноколличественность: Нормальное распределение характеризуется одной количественной характеристикой - ее средним значением. Это число представляет собой центр распределения и является его самым типичным значением.
- Нормальность: Нормальное распределение стремится к тому, чтобы большинство значений сосредотачивались вокруг среднего значения и уменьшались с возрастанием расстояния от него. Это означает, что хвосты распределения постепенно убывают и стремятся к нулю.
- Простота формы: Форма нормального распределения проста и легко представляется на графике в виде колокольчика. Это делает его удобным для визуализации и понимания.
- Коэффициент вариации: Нормальное распределение характеризуется коэффициентом вариации, который позволяет измерить, насколько сильно значения разбросаны вокруг среднего значения. Чем меньше коэффициент вариации, тем более концентрированы значения вокруг среднего, и наоборот.
Понимание основных характеристик нормального распределения позволяет ученым и статистикам анализировать данные, предсказывать вероятности и строить модели, основанные на этом распределении. Нормальное распределение имеет множество практических применений и широко используется во многих науках и областях, включая физику, экономику, биологию и социальные науки.
Примеры применения нормального закона распределения
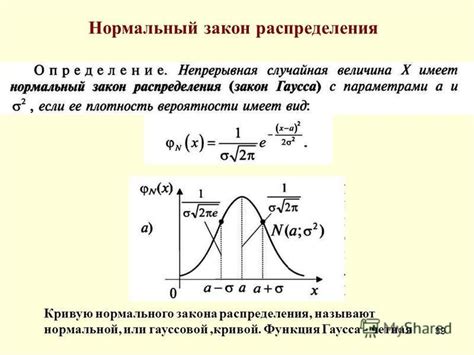
Финансы и экономика: Нормальное распределение используется для моделирования финансовых рынков и предсказания изменений цен на акции, валюты и другие финансовые инструменты. Многие модели риска основываются на предположении о нормальном распределении доходности активов.
Медицина: Нормальное распределение может быть использовано для анализа различных медицинских данных, таких как показатели здоровья пациентов, вес новорожденных или уровень холестерина в крови. Это позволяет определить норму для конкретного параметра и выявить отклонения от этой нормы.
География: Нормальное распределение может быть использовано для анализа данных о различных географических явлениях, таких как распределение осадков, температуры или высоты над уровнем моря. Это помогает определить типичные значения и степень отклонения от них.
Инженерия: Нормальное распределение используется для анализа и моделирования различных инженерных данных, таких как измерения размеров деталей, температура в разных точках системы или напряжение в электрической сети. Это помогает в определении статистических параметров и обнаружении нештатных ситуаций.
Это лишь некоторые примеры применения нормального закона распределения. Благодаря своей универсальности и математическим свойствам, нормальное распределение находит применение во многих областях и помогает исследователям и специалистам делать более точные прогнозы и принимать обоснованные решения на основе статистических данных.
Центральная предельная теорема и нормальный закон распределения

Нормальный закон распределения, также известный как гауссовское распределение, является одним из самых фундаментальных распределений в статистике. Он характеризуется своей симметрией и колоколообразной формой. График нормального распределения образует симметричную кривую, которая имеет один пик и тянется бесконечно в обе стороны. Нормальное распределение полностью определяется двумя параметрами: математическим ожиданием (средним) и стандартным отклонением.
ЦПТ говорит нам, что независимо от формы исходного распределения, сумма большого числа случайных величин, взятых из этого распределения, будет приближаться к нормальному распределению. Более точно, ЦПТ утверждает, что сумма большого числа случайных величин будет иметь нормальное распределение с тем же математическим ожиданием и стандартным отклонением, что и исходное распределение, деленными на квадратный корень из количества слагаемых.
Доказательство ЦПТ основано на применении характеристических функций случайных величин и использовании теоремы об обратном преобразовании Фурье. Однако, для практических целей, можно просто принять ЦПТ как факт и использовать его для приближения распределения суммы случайных величин нормальным распределением. Это позволяет проводить множество статистических исследований и прогнозирований, так как нормальное распределение широко применяется в моделировании данных и анализе.
Свойства нормального закона распределения
1. Центральная предельная теорема: Одно из ключевых свойств нормального распределения заключается в том, что сумма или среднее большого числа независимых и одинаково распределенных случайных величин сходится к нормальному распределению, даже если сами величины не являются нормально распределенными. Это является основой для использования нормального распределения в математической статистике.
2. Форма колокола: Нормальное распределение имеет симметричную колоколообразную форму с концентрацией значений вокруг среднего. Это означает, что вероятность значений, близких к среднему, составляет основную часть распределения, а вероятность значений, удаленных от среднего, уменьшается.
3. Параметры среднего и дисперсии: Нормальное распределение полностью определяется двумя параметрами: средним (μ) и дисперсией (σ²). Среднее значение определяет положение пика колокола, а дисперсия характеризует его ширину. Часто используют также стандартное отклонение (σ), которое является квадратным корнем из дисперсии.
4. 68-95-99.7 правило: Одним из важных свойств нормального распределения является то, что около 68% значений находятся в пределах одного стандартного отклонения от среднего, около 95% - в пределах двух стандартных отклонений, и около 99.7% - в пределах трех стандартных отклонений. Это правило позволяет легко оценить вероятность появления значений в определенном интервале.
5. Применимость в реальных явлениях: Нормальное распределение широко применимо для моделирования различных явлений в природе, экономике, физике, биологии и других областях. Многие случайные величины, такие как рост людей, вес, уровень интеллекта и т.д., подчиняются нормальному распределению или могут быть приближены этим законом.
Как проверить, соответствует ли случайная величина нормальному закону распределения?

Для того чтобы проверить, соответствует ли случайная величина нормальному закону распределения, можно использовать несколько статистических тестов.
Один из таких тестов - тест Колмогорова-Смирнова. Он позволяет сравнить эмпирическую функцию распределения с теоретической функцией распределения и оценить статистическую значимость различий между ними.
Другой распространенный тест - тест Шапиро-Уилка. Он основан на сравнении коэффициента асимметрии и эксцесса эмпирического распределения с их теоретическими значениями для нормального распределения.
Кроме того, можно использовать графические методы, такие как гистограммы и квантиль-квантильные графики (Q-Q plots), для визуальной оценки соответствия распределения данных нормальному.
Более продвинутые методы, такие как анализ Лиллиефорса, тест Андерсона-Дарлинга и тест Жарка-Бера, также могут быть использованы для проверки нормальности распределения.
Необходимо отметить, что результаты этих тестов могут быть влияние выборкой данных и размером выборки. Поэтому важно проводить несколько тестов и анализировать результаты в комплексе.
| Тест | Описание |
|---|---|
| Тест Колмогорова-Смирнова | Сравнивает эмпирическую функцию распределения с теоретической |
| Тест Шапиро-Уилка | Основан на сравнении коэффициента асимметрии и эксцесса |
| Графические методы | Гистограммы и квантиль-квантильные графики |
| Анализ Лиллиефорса | Тест на нормальность с использованием эмпирического кумулятивного распределения |
| Тест Андерсона-Дарлинга | Сравнивает функцию распределения с функцией распределения нормального распределения |
| Тест Жарка-Бера | Основан на анализе коэффициентов асимметрии и эксцесса |
Достоинства и недостатки использования нормального закона распределения
| Достоинства | Недостатки |
|---|---|
1. Широкое применение. Нормальное распределение используется для моделирования различных природных и социальных явлений. Оно применимо во множестве областей, включая физику, экономику, биологию, психологию и другие. Благодаря этому, нормальное распределение является универсальным инструментом для анализа данных. | 1. Ограничения применимости. |
2. Симметричность и нормальность. Нормальное распределение является симметричным относительно среднего значения и имеет колоколообразную форму. Это облегчает интерпретацию и анализ данных, так как параметры распределения явно описывают основные характеристики выборки, включая среднее значение и стандартное отклонение. | 2. Неустойчивость к выбросам. |
3. Центральная предельная теорема. Нормальное распределение является основным инструментом в рамках центральной предельной теоремы. Согласно этой теореме, сумма большого количества независимых случайных переменных, вне зависимости от их распределения, приближается к нормальному распределению. Это позволяет использовать нормальное распределение для оценки среднего значения и стандартной ошибки при анализе выборочных данных. | 3. Неявность и упрощение. Нормальное распределение является упрощенной моделью реальных данных. Использование нормального закона подразумевает неявное предположение о нормальности данных и их независимости. Однако, в реальных ситуациях это предположение может быть неверным, что может привести к неточностям в анализе и оценках распределения. |




