Решение системы неравенств является одной из основных задач в математике и может иметь важные применения в различных областях науки, техники и экономики. Но что делать, если требуется найти не просто любое решение, а наименьшее целое решение? В этой статье мы рассмотрим принципы поиска такого решения и приведем несколько примеров для наглядности.
Одним из основных принципов при поиске наименьшего целого решения системы неравенств является перебор значений переменных в целочисленном диапазоне. Идея заключается в том, чтобы начать с наименьшего возможного значения и постепенно увеличивать его до тех пор, пока не будет найдено удовлетворяющее условиям решение. При этом важно учитывать границы диапазона, заданные неравенствами, чтобы не выполнять бесконечное число итераций.
Но как определить, что найденное решение является наименьшим? Для этого можно использовать методы сравнения и проверки всех возможных вариантов решений. Важно помнить, что для определения наименьшего решения может потребоваться сравнение нескольких параметров или значений. Это значительно усложняет задачу, но при правильной организации поиска можно добиться точных результатов.
Принципы решения системы неравенств
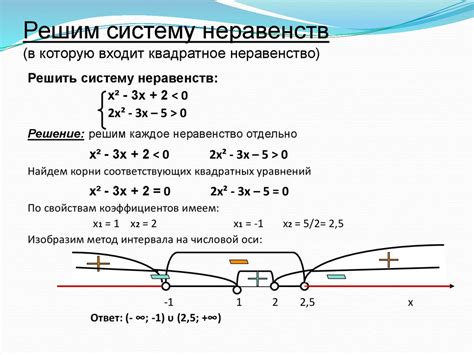
Решение системы неравенств состоит в нахождении набора значений переменных, которые удовлетворяют всем неравенствам системы. При этом нас интересуют только целочисленные решения, то есть такие наборы значений, где все переменные принимают целочисленные значения.
Принципы решения системы неравенств можно сформулировать следующим образом:
- Преобразование системы неравенств к каноническому виду. Для этого все неравенства приводятся к виду: переменная <= константа или переменная >= константа. При этом переменные могут быть только неотрицательными.
- Построение таблицы решений. Создается таблица, где каждая строка соответствует одному неравенству, а каждый столбец соответствует одной переменной. В ячейках таблицы записываются значения переменных, которые удовлетворяют соответствующему неравенству.
- Поиск минимального целочисленного решения. Необходимо найти такую строку таблицы решений, где значения переменных являются наименьшими среди всех строк. Это и будет минимальным целочисленным решением системы неравенств.
Принципы решения системы неравенств могут быть наглядно представлены с помощью примера. Рассмотрим, например, следующую систему неравенств:
| 2x + 3y <= 10 | x >= 0 |
| 4x + y >= 6 | y >= 0 |
Сначала приведем все неравенства к каноническому виду:
| x + y <= 5 | x >= 0 |
| 4x + y >= 6 | y >= 0 |
Затем построим таблицу решений:
| x | y |
|---|---|
| 0 | 5 |
| 0 | 6 |
| 1 | 4 |
| 1 | 5 |
| 1 | 6 |
| 2 | 3 |
| 2 | 4 |
| 2 | 5 |
| 3 | 3 |
Наконец, найдем минимальное целочисленное решение, которое будет равно x = 2 и y = 3. Таким образом, система неравенств имеет минимальное целочисленное решение x = 2, y = 3.
Нахождение наименьшего целого решения

Для решения системы неравенств и нахождения наименьшего целого решения необходимо использовать принципы целочисленного программирования. Подобные системы могут возникать в различных задачах оптимизации, где требуется найти наименьшее возможное значение переменных, удовлетворяющих определенным условиям.
Для начала, система неравенств должна быть приведена к виду, где все переменные ограничены только снизу. Это делается путем вычитания одной и той же константы из обеих частей каждого неравенства до тех пор, пока все переменные не будут ограничены только снизу. Затем, мы можем добавить новую переменную, называемую "вспомогательной переменной", которая будет участвовать в системе неравенств как и остальные переменные.
Далее, следует составить целочисленную линейную функцию, которую нужно минимизировать. Она состоит из суммы всех переменных с соответствующими коэффициентами. Целью является минимизация этой функции.
Задачу можно решить с помощью методов целочисленного программирования, таких как метод ветвей и границ или метод динамического программирования. Эти методы с помощью алгоритмов позволяют перебрать все возможные варианты значений переменных и выбрать наименьшее целое решение системы неравенств.
Итак, нахождение наименьшего целого решения системы неравенств требует использования принципов целочисленного программирования. Необходимо привести систему к виду, где все переменные ограничены только снизу, составить целочисленную линейную функцию и использовать методы целочисленного программирования для нахождения наименьшего целого решения.
Алгоритм поиска наименьшего целого решения

Для поиска наименьшего целого решения системы неравенств следует использовать следующий алгоритм:
- Составить систему неравенств в стандартной форме, то есть выразить все переменные только через положительные целые значения.
- Заменить все переменные расширенным набором из двух переменных: одну переменную для значения целой части и другую переменную для значения дробной части.
- Перебрать все возможные комбинации положительных целых значений для переменных.
- Для каждой комбинации вычислить значения переменных, используя значения целой и дробной частей.
- Проверить выполнение всех условий системы неравенств для каждой комбинации значений переменных.
- Найти наименьшее значение целой части, которое удовлетворяет всем условиям системы неравенств. Если такого значения нет, то система неравенств не имеет целочисленного решения.
Применение этого алгоритма позволяет найти наименьшее целое решение системы неравенств, если такое решение существует. Дальнейшее увеличение значения целой части будет приводить к нарушению хотя бы одного из условий системы неравенств.
Примеры решения системы неравенств
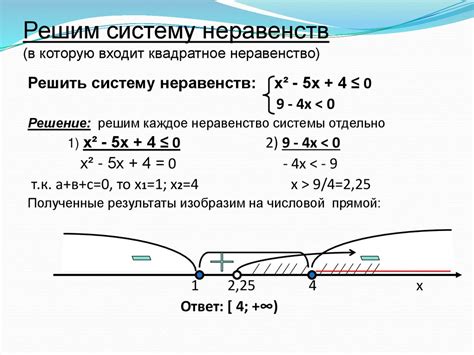
Для более наглядного объяснения принципов решения системы неравенств, рассмотрим несколько примеров:
Пример 1:
Рассмотрим систему неравенств:
{3x - 2y >= 5
{-4x + y > 3
Для решения данной системы неравенств можно использовать графический метод. Сначала построим график обеих неравенств на координатной плоскости:
На графике обозначены области, удовлетворяющие каждому из неравенств. Точка пересечения этих областей будет являться решением системы неравенств. В данном случае, точка пересечения равна (2, -1).
Пример 2:
Рассмотрим систему неравенств:
{2x + 3y >= 6
{-x + y >= 2
Для решения данной системы неравенств можно использовать метод подстановки. Подставим выражение y = 2 + x из второго неравенства в первое, получим:
2x + 3(2 + x) >= 6
Решая данное уравнение, получим значение x = 1. Подставим это значение во второе неравенство:
-1 + y >= 2
Решая данное уравнение, получим значение y = 3. Таким образом, решение системы неравенств равно (1, 3).
Таким образом, решение системы неравенств может быть найдено с использованием различных методов, таких как графический метод, метод подстановки, метод исключения и другие. Выбор метода зависит от конкретной системы неравенств и может быть определен на основе удобства и эффективности.
Полезные советы для решения системы неравенств
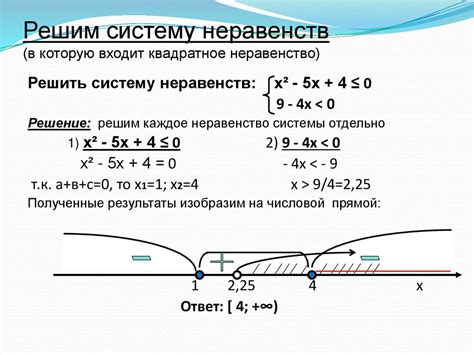
Решение системы неравенств может быть сложной задачей, но с правильным подходом можно достичь желаемого результата. Вот несколько полезных советов, которые помогут вам решить систему неравенств эффективно и без ошибок:
- Анализируйте каждое неравенство по отдельности. Изучите его знак и диапазон допустимых значений переменных. Это поможет определить, какие значения переменных удовлетворяют неравенству.
- Используйте графический метод для визуализации системы неравенств. Нанесите неравенства на координатную плоскость и найдите пересечение областей, которые удовлетворяют всем неравенствам. Это поможет вам визуально представить решение системы.
- Используйте алгебраические методы для точного определения решения системы. Применяйте различные методы упрощения выражений, замены переменных и преобразования неравенств, чтобы сократить систему к минимуму и найти решение.
- Проверяйте полученное решение, подставляя его в каждое неравенство системы. Убедитесь, что все неравенства выполняются для выбранных значений переменных. Если хотя бы одно неравенство не выполняется, это означает, что решение некорректно.
- Не забывайте о граничных условиях. Если неравенство содержит знак равенства, учтите, что это может повлиять на решение. Проверьте все возможные варианты, включая граничные значения и исключающие значения.
Следуя этим полезным советам, вы сможете решать системы неравенств более эффективно и получать точные результаты. Помните, что решение может быть не единственным, и ваша задача – найти все возможные значения переменных, которые удовлетворяют системе неравенств.




