Касательная – одна из основных геометрических фигур, которая играет важную роль в изучении окружностей. Она представляет собой прямую, которая соприкасается с окружностью только в одной точке. Касательная к окружности имеет ряд особенностей и свойств, которые пригодятся в геометрии и применяются в различных задачах.
Одной из основных особенностей касательной является то, что она перпендикулярна радиусу, проведенному в точке касания. То есть, угол, образованный касательной и радиусом в точке касания, равен 90 градусов. Это свойство позволяет использовать касательную для решения задач, связанных с построением прямоугольных треугольников и нахождением расстояний между точками на окружности.
Еще одно важное свойство касательной состоит в том, что она делит хорду, соединяющую точку касания с любой другой точкой окружности, на две равные части. Это означает, что отрезки хорды, находящиеся по разные стороны от касательной, имеют одинаковую длину. Это свойство касательной широко применяется для нахождения неизвестных длин отрезков или решения задач на равноудаленность точек от прямой.
Касательная к окружности: определение и свойства

Первое свойство касательной заключается в том, что она всегда касается окружности в единственной точке. Это означает, что если взять любую прямую и двигать ее вокруг окружности, то только одно положение прямой приведет к касанию.
Второе свойство заключается в том, что касательная перпендикулярна радиусу, проведенному в точке касания. Это означает, что угол между радиусом и касательной равен 90 градусам.
Третье свойство связано с прямоугольными треугольниками. Если провести касательную к окружности и соединить точку касания с центром окружности, то получится прямоугольный треугольник. Это происходит из-за свойства перпендикулярности касательной и радиуса.
Касательная к окружности имеет множество применений в геометрии. Она используется при решении задач на построение окружности, в доказательствах теорем о взаимном расположении прямых и окружностей, а также в задачах на нахождение значений углов и длин отрезков.
Касательная к окружности: что это такое?
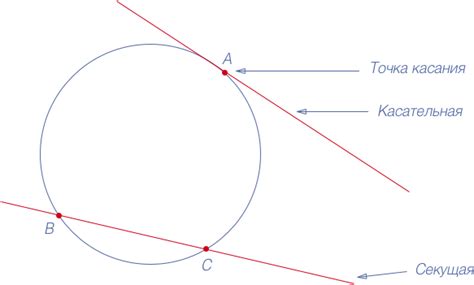
Касательная к окружности имеет несколько свойств:
- Касательная к окружности является прямой.
- Она касается окружности только в одной точке.
- Касательная перпендикулярна радиусу, проведенному в точке касания.
Касательная к окружности может быть использована для определения различных характеристик окружности. Например, она может быть использована для нахождения точки пересечения окружности с другой прямой или для нахождения наклона касательной в данной точке.
Касательная к окружности играет важную роль в геометрии и в различных областях науки и техники. Она является основой для изучения кривых и окружностей, а также для решения различных задач и проблем, связанных с окружностями.
Касательная к окружности: свойства и особенности
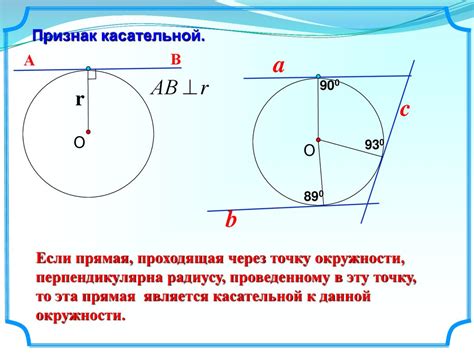
Основные свойства касательной к окружности:
- Касательная к окружности всегда перпендикулярна радиусу, проведенному к точке касания. Это означает, что угол между касательной и радиусом равен 90 градусов.
- Точка касания является точкой пересечения радиуса и касательной. Она лежит на одной прямой с центром окружности и точкой касания.
- Если из точки касания до центра окружности провести отрезок, то он будет равен радиусу окружности. Это свойство следует из определения касательной.
Касательная к окружности также обладает рядом других особенностей, которые важны при решении геометрических задач. Например:
- Если две окружности касаются внешним образом, то линия, соединяющая их центры, является касательной для каждой из окружностей в точке касания.
- Если две окружности касаются внутренним образом, то линия, соединяющая их центры, также является касательной для каждой из окружностей в точке касания.
Использование касательных к окружности широко распространено в геометрии и находит применение в задачах построения и вычисления различных параметров окружностей.
Применение касательной к окружности в геометрии
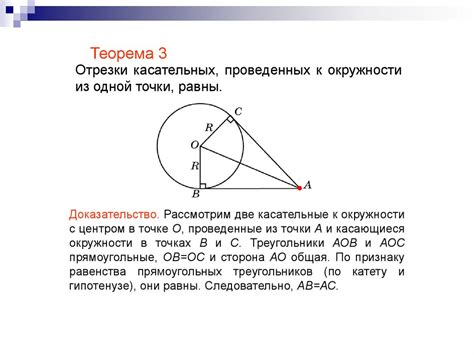
1. Поиск точек пересечения: Касательная позволяет найти точки пересечения окружности с другими фигурами, такими как прямые, заданные уравнениями. Например, с помощью касательной можно найти точки пересечения окружности с прямой, проходящей через ее центр.
2. Решение геометричеких задач: Касательная используется для решения различных геометрических задач. Например, с помощью касательной можно определить внутренний и внешний углы между прямой и окружностью, а также провести прямую, параллельную заданной, касающуюся окружности.
3. Исследование свойств окружностей: Касательные помогают изучить различные свойства окружностей, такие как радиус, диаметр, хорда и дуги. Например, касательная, проведенная к окружности из внешней точки, делит хорду на две равные части.
4. Разработка математических моделей: Касательные используются для создания математических моделей, которые описывают окружности и их свойства. Эти модели широко применяются в различных областях науки и техники.



