График функции является важным элементом в математике, который позволяет визуализировать зависимость между двумя переменными. Один из наиболее простых и интересных типов графиков – график функции игрек равно икс. Он представляет собой линию, которая проходит через все точки, у которых значения игрек (y) равны значениям икс (x).
График функции игрек равно икс имеет некоторые особенности. Во-первых, он всегда проходит через начало координат (0,0), так как значения игрек равны значениям икс. Во-вторых, такой тип графика симметричен относительно прямой y=x. Это значит, что если поменять местами значения игрек и икс, то график останется неизменным. В-третьих, график функции игрек равно икс представляет собой прямую линию, которая может быть наклонной или вертикальной в зависимости от значения коэффициента наклона функции.
Пример графика функции игрек равно икс может быть представлен следующим образом: если значения икс равны 1, 2, 3, то значения игрек также будут равны 1, 2, 3. Таким образом, точки на графике будут следующими: (1,1), (2,2), (3,3). В результате получится прямая линия, проходящая через все эти точки. Если поменять местами значения икс и игрек, то график останется таким же. Такой график может быть использован для моделирования зависимости одной переменной от другой, а также для построения простых математических алгоритмов.
Особенности графика функции игрек равно икс

Особенность этого графика заключается в том, что значение координаты y всегда равно значению координаты x. То есть, любая точка графика данной функции имеет координаты (x, x).
Такой график имеет следующие особенности:
- Прямая линия: график функции игрек равно икс представляет собой прямую линию, которая проходит через начало координат (0, 0) и образует угол 45 градусов с положительным направлением осей координат.
- Единичный наклон: угловой коэффициент этой прямой равен 1, так как значение координаты y всегда равно значению координаты x.
- Симметричность: график функции является симметричным относительно оси y=x. То есть, если перенести точку графика с координатами (x, y) на ось y=x, получим точку с координатами (y, x), которая также принадлежит графику функции.
- Уникальность: каждая точка на графике функции игрек равно икс имеет уникальные координаты (x, x), что означает, что каждое значение x соответствует только одному значению y.
Пример графика функции игрек равно икс представлен в таблице ниже:
| Значение x | Значение y |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
Значения функции при разных значащих цифрах
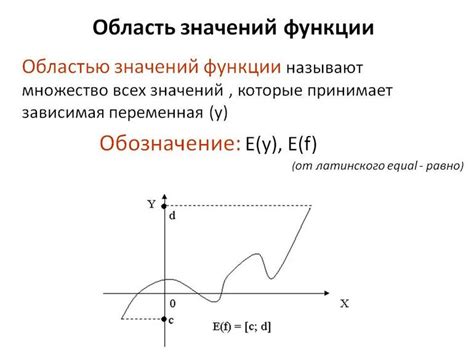
Функция игрек равно икс представляет собой простой график, на котором все значения y (игрек) равны соответствующим значениям x (икс). Таким образом, на графике данной функции мы наблюдаем прямую линию, проходящую через начало координат (0, 0) и образующую угол 45 градусов с положительным направлением оси x.
Значения функции игрек равно икс могут быть представлены в виде таблицы:
| Значащая цифра x (икс) | Значение функции y (игрек) |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
Таким образом, при значащих цифрах от 1 до 9 значение функции y (игрек) будет равно соответствующей значащей цифре x (икс).
Примеры:
- При x = 2, y = 2
- При x = 5, y = 5
- При x = 8, y = 8
Нулевая производная
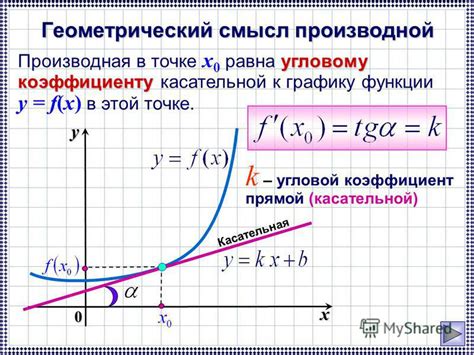
Если производная функции равна нулю, то эта точка может быть экстремумом: максимумом или минимумом функции. Например, если функция имеет нулевую производную в точке x = a, то это может означать, что функция имеет локальный минимум или максимум в этой точке.
Нулевая производная может также указывать на точки перегиба функции. Перегиб функции – это точка, в которой меняется выпуклость или вогнутость графика. Если производная функции равна нулю и меняет знак в данной точке, то это говорит о существовании перегиба в этой точке.
Примером функции с нулевой производной может служить функция y = x3. Ее производная равна нулю в точке x = 0, что указывает на существование перегиба в этой точке.
Примеры графиков функции игрек равно икс
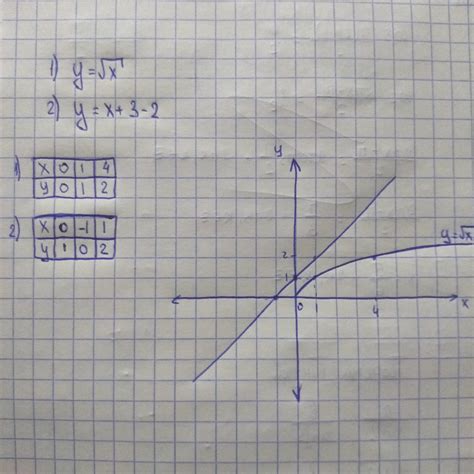
Функция игрек равно икс представляет собой особый случай графика, где каждая точка на плоскости имеет координаты (x, x). Таким образом, функция y = x описывает линию, проходящую через начало координат под углом 45 градусов.
На приведенном ниже графике показана функция игрек равно икс в интервале от -10 до 10:
| x | y |
|---|---|
| -10 | -10 |
| -5 | -5 |
| 0 | 0 |
| 5 | 5 |
| 10 | 10 |
Как видно из таблицы, значение y всегда равно значению x, что и обуславливает название функции "игрек равно икс". Этот график имеет вид прямой, проходящей через начало координат и обладающей прямой пропорциональности.
Математическую связь функции игрек равно икс можно представить следующим уравнением:
y = x
Примеры графиков функции игрек равно икс можно найти во многих областях, включая физику, экономику и графическое представление данных. Такие графики могут быть использованы для отображения зависимости одной переменной от другой и представления линейных трендов.



