Равновозможные события – это основной понятие в теории вероятности, которое имеет большое значение при расчете вероятностей различных событий. Обычно в контексте равновозможных событий говорят о том, что все события имеют одинаковые шансы на возникновение.
В теории вероятности равновозможные события обладают несколькими ключевыми чертами. Прежде всего, каждое из них имеет некоторую вероятность. Кроме того, вероятности всех равновозможных событий должны быть одинаковыми. Это значит, что шансы на возникновение каждого события равны между собой.
Примером равновозможных событий может служить бросок правильной монеты. В этом случае у нас есть два равновозможных события – выпадение герба и выпадение решки. Вероятность выпадения герба равна вероятности выпадения решки и составляет 0,5 или 50%.
Концепция равновозможных событий широко применяется в различных областях науки и практики, включая статистику, физику и экономику. Если мы имеем дело с несколькими равновозможными событиями, то вероятность каждого из них может быть легко рассчитана с помощью простого математического подхода.
Равновозможные события в теории вероятности

Если у нас имеется некоторый случайный эксперимент, то различные исходы этого эксперимента называются событиями. Если данные события имеют одинаковую вероятность наступления, то они считаются равновозможными.
Наиболее простым примером равновозможных событий может служить подбрасывание честной монеты. В данном случае есть всего два равновозможных исхода - выпадение орла или решки. Так как у обоих исходов равная вероятность наступления (половинная), то события "выпадение орла" и "выпадение решки" считаются равновозможными.
Определение равновозможных событий важно для построения математической модели вероятности. При проведении вероятностных расчетов, где все события равновозможны, используются равномерные распределения.
Равновозможные события представляют особый случай в теории вероятности, где вероятность каждого события равна некоторой константе, определяемой числом всех возможных равновозможных исходов эксперимента.
Определение и особенности
Основная особенность равновозможных событий заключается в том, что вероятность возникновения каждого из них равна. Если у нас есть n равновозможных событий, то вероятность возникновения каждого события равна 1/n. Например, при броске честной монеты есть два равновозможных события – выпадение орла и выпадение решки. Вероятность возникновения каждого из этих событий равна 1/2.
Другой важной особенностью равновозможных событий является то, что сумма вероятностей всех равновозможных событий всегда равна единице. Это следует из того, что все равновозможные события являются исчерпывающими – одно из них обязательно произойдет.
Равновозможные события широко используются в теории вероятности для моделирования различных случайных процессов. Они позволяют с учетом вероятностных соотношений предсказывать возможные исходы и оценивать вероятность появления определенных событий.
Примеры равновозможных событий

В теории вероятности равновозможными событиями называются те события, которые имеют одинаковую вероятность выпадения. Ниже приведены несколько примеров равновозможных событий:
| Пример | Объяснение |
|---|---|
| Подбрасывание монеты | При подбрасывании монеты есть всего два равновозможных исхода: выпадение "орла" или "решки". Оба исхода имеют одинаковую вероятность - 50%. |
| Бросание кубика | При бросании шестигранного кубика считается, что все шесть граней равновозможны и имеют одинаковую вероятность выпадения - 1/6. |
| Выбор карты из колоды | Если из полной колоды карт выбирается одна карта без возвращения, то каждая карта имеет одинаковую вероятность быть выбранной, так как в начале у каждой карты равновозможные шансы быть выбранной. |
| Выбор шаров из урны | При выборе шаров из урны с одинаковыми шансами выпадения каждого цвета шаров, все цвета считаются равновозможными событиями. |
Все эти примеры соответствуют определению равновозможных событий, так как для каждого события вероятность выпадения одинакова и составляет 50% или 1/6 или 1/n, где n - число возможных исходов.
Вероятность равновозможных событий

Для определения вероятности равновозможных событий необходимо поделить количество благоприятных исходов на общее количество возможных исходов.
Например, если у нас есть игральная кость, то вероятность выпадения каждой грани будет равна 1/6, так как у кости 6 граней и каждая грань имеет одинаковые шансы выпасть.
Еще одним примером является выбор карты из колоды. Если в колоде 52 карты и мы выбираем одну карту, то вероятность выбрать определенную карту равна 1/52, так как каждая карта имеет одинаковые шансы быть выбранной.
Вероятность равновозможных событий имеет важное значение в теории вероятности, так как позволяет определить вероятность наступления конкретного события на основе его равновозможности с другими событиями.
Например, если у нас есть два равновозможных события A и B, то вероятность наступления события A или B будет равна сумме их индивидуальных вероятностей.
Таким образом, вероятность равновозможных событий является ключевым понятием в теории вероятности и используется для определения вероятности наступления различных событий.
Условия равновозможности событий

Чтобы события были равновозможными, необходимо выполнение следующих условий:
- Все возможные исходы должны быть равновероятными. То есть каждый исход должен иметь одинаковую вероятность.
- События должны быть взаимоисключающими. Это означает, что если происходит одно событие, то другое не может произойти одновременно.
Если эти условия выполняются, то вероятность каждого события может быть рассчитана по формуле:
P(A) = 1/n, где P(A) - вероятность события A, n - количество равновозможных исходов.
Например, если у нас есть справедливая игральная кость, то вероятность выпадения каждого из шести возможных значений (от 1 до 6) будет равна 1/6. В этом случае все события, соответствующие выпадению каждого значения, являются равновозможными.
Связь равновозможности с частотностью
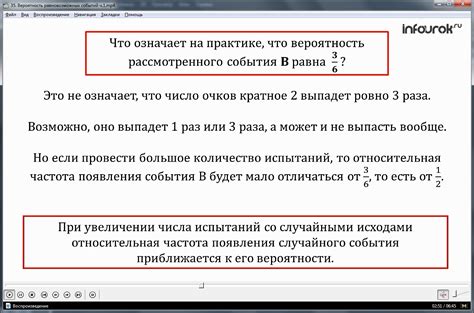
В теории вероятности равновозможные события имеют прямую связь с частотностью. Если два события равновозможны, то они имеют одинаковую вероятность выпадения. Вероятность события можно интерпретировать как отношение количества благоприятных исходов к общему количеству возможных исходов.
Связь с равновозможностью основана на предположении, что частотность событий в большой выборке будет стремиться к их вероятностям. То есть, если провести большое количество испытаний, количество выпадения каждого события будет приближаться к его вероятности.
Например, при подбрасывании правильной монеты вероятность выпадения орла или решки равна 0.5 каждому событию. Если провести большое количество подбрасываний, то количество выпадения орла и решки будет примерно равномерным.
Равновозможные события и независимость

События могут быть как независимыми, так и зависимыми друг от друга. Независимые события - это такие события, при которых наступление одного из них не влияет на вероятность наступления другого. Например, выбрасывание грани монеты и выпадение орла на одной стороне не зависит от выпадения решки на другой стороне.
Независимость событий является важным понятием в теории вероятности, так как позволяет упростить вычисления и анализ вероятностей. Если два события являются независимыми, то вероятность их совместного наступления равна произведению их вероятностей. Например, если вероятность выпадения орла на монете равна 0.5, а вероятность выпадения решки равна 0.5, то вероятность выпадения орла и решки одновременно равна 0.5 * 0.5 = 0.25.
Однако, не все события являются независимыми. Зависимые события - это такие события, при которых наступление одного из них влияет на вероятность наступления другого. Например, если из колоды карт вытянута черная карта, то вероятность вытащить красную карту будет уменьшаться.
Понимание равновозможных событий и их независимости является ключевым для правильного применения теории вероятности в различных областях, таких как математика, статистика, физика, экономика и другие.
Равновозможные события и случайные величины

Случайные величины в теории вероятности представляют собой величины, значения которых зависят от исхода случайного эксперимента. Случайные величины могут принимать разные значения в зависимости от того, какой исход эксперимента произошел.
Применение равновозможных событий в реальных задачах
Равновозможные события в теории вероятности обеспечивают простоту и удобство в решении реальных задач. В более простых случаях, где все события равновозможны, можно использовать простые формулы для расчета вероятностей. Это позволяет проводить анализ и принимать решения на основе вероятностных закономерностей, которые имеются в реальном мире.
Примером использования равновозможных событий может служить задача о бросании игральной кости. В этом случае имеется шесть равновозможных исходов, соответствующих выпадению каждой из шести граней кости. Вероятность выпадения конкретной грани равна 1/6. Таким образом, с помощью простой формулы можно рассчитать вероятность выпадения любой из граней.
В другом примере, равновозможные события могут использоваться для определения вероятности успеха в случайных экспериментах. Например, при проведении серии испытаний нового лекарства на группе пациентов, можно считать каждое испытание равновозможным событием. Исход успешного лечения является одним из возможных исходов, поэтому вероятность успеха можно выразить как отношение числа успешных испытаний к общему числу испытаний.
Также равновозможные события могут применяться для анализа вероятности выигрыша в различных азартных играх, таких как игры в казино. В этом случае каждый исход игры может считаться равновозможным событием, и вероятность выигрыша может быть рассчитана как отношение числа выигрышных исходов к общему числу исходов.
Использование равновозможных событий в реальных задачах позволяет проводить анализ вероятности и принимать обоснованные решения на основе вероятностных закономерностей. Это может быть полезным инструментом при прогнозировании, планировании и принятии решений в различных областях, включая медицину, экономику и игровую индустрию.
В теории вероятности равновозможные события играют важную роль. Равновозможные события представляют собой события, которые имеют одинаковую вероятность наступления. Это означает, что вероятность каждого из этих событий равна другим равновозможным событиям.
Определение равновозможных событий является ключевым понятием для установления связи между вероятностями различных событий. Если у нас есть несколько равновозможных событий, мы можем использовать это знание для определения вероятностей других событий.
Из равновозможности событий следует, что вероятность каждого из них равна 1/количество равновозможных событий. Например, если у нас есть 4 равновозможных события, то вероятность каждого из них равна 1/4 или 0,25 (или 25%).
Знание о равновозможности событий также позволяет нам использовать простой принцип сложения вероятностей. Если у нас есть два равновозможных события A и B, то вероятность события A или B равна сумме вероятности события A и вероятности события B. Это позволяет нам вычислять вероятности сложных событий на основе вероятностей равновозможных событий.
Определение равновозможных событий имеет большое значение в повседневной жизни и в научных исследованиях. Оно позволяет нам анализировать вероятность различных событий и принимать основанные на вероятности решения.



