В современном мире, где математика играет всё более важную роль в различных областях науки и технологий, понимание того, как определить математическую модель задачи, становится неотъемлемой частью образования и науки. Математическая модель представляет собой абстракцию реальной системы или процесса, которая помогает описать и предсказывать его поведение и свойства. От определения математической модели зависят дальнейшие исследования и применение математических методов решения конкретных задач.
Первым шагом в процессе построения математической модели является определение важных понятий и параметров, которые будут участвовать в описании системы. Важно выделить основные составляющие, определить их свойства и взаимодействие между собой. Изучение реального объекта или процесса, а также сбор и анализ доступных данных являются неотъемлемой частью этого этапа.
После определения важных параметров следует выбор уравнений и функций, которые будут использоваться для описания свойств и закономерностей системы. Это могут быть линейные или нелинейные уравнения, дифференциальные уравнения, алгебраические уравнения и другие математические выражения. Однако важно помнить, что модель должна быть адекватной и отражать реальность, поэтому выбор уравнений должен быть обоснованным.
Для лучшего понимания, как определить математическую модель задачи, рассмотрим пример. Предположим, у нас есть задача о поиске оптимального пути между двумя точками в городе. В качестве важных параметров мы можем выбрать расстояние между точками, время, затрачиваемое на передвижение, пропускную способность дорог и другие. Для описания свойств системы можно использовать функцию, которая будет учитывать расстояние и время преодоления пути, а также другие факторы, влияющие на выбор оптимального маршрута.
Задачи и модели: важные понятия
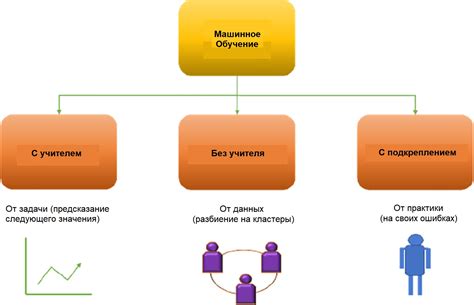
Математическая модель – это абстрактное представление реального объекта или процесса с использованием математических понятий и операций. Математические модели позволяют анализировать и решать сложные задачи, предсказывать поведение системы и оптимизировать процессы.
Параметры – это переменные, описывающие свойства и характеристики объектов или процессов в математической модели. Значения параметров могут варьироваться и влиять на результаты моделирования.
Переменные – это величины, которые могут изменяться в рамках модели. Они могут зависеть от параметров и других переменных, и изменение их значений влияет на результаты моделирования.
Функции – это математические выражения, описывающие зависимости между переменными и параметрами в математической модели. Функции могут представлять различные виды зависимостей, такие как прямая или обратная пропорциональность, экспоненциальный рост и другие.
Ограничения – это условия или ограничения, налагаемые на переменные и параметры в математической модели. Ограничения могут быть как физическими, так и логическими, ограничивая диапазон и вариативность значений.
Оптимизация – это процесс нахождения наилучших значений для переменных, удовлетворяющих ограничениям и минимизируя или максимизируя целевую функцию. Оптимизация используется для достижения наилучшего решения или планирования в различных областях науки, инженерии и бизнесе.
Примеры задач и математических моделей включают в себя: моделирование популяции животных, моделирование распространения эпидемий, оптимизация маршрутов доставки, прогнозирование погоды, решение уравнений в физике и многое другое. Математические модели могут быть применены практически во всех областях деятельности, где требуется анализ и оптимизация процессов.
Определение задачи и моделирование
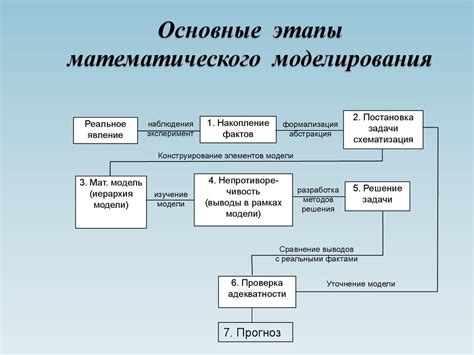
После определения задачи происходит моделирование, которое заключается в создании абстрактной математической модели, представляющей реальную ситуацию. Математическая модель должна содержать все необходимые элементы для решения задачи, такие как переменные, уравнения и условия.
Моделирование включает выбор подходящего математического описания задачи, а также выбор методов и инструментов для ее решения. Это может включать применение алгоритмов, статистических методов, теории оптимизации и других математических инструментов.
Основная цель моделирования - предоставить абстрактную математическую структуру, которая позволяет анализировать и решать задачу. Математическая модель должна быть достаточно точной, чтобы представлять суть реальной ситуации, и при этом достаточно простой, чтобы было возможно проводить вычисления и анализировать результаты.
Примеры задач, которые могут быть решены с помощью математического моделирования, включают оптимизацию расписания, планирование производства, прогнозирование финансовых показателей, моделирование трафика и многие другие. Математическое моделирование является мощным инструментом для анализа и решения разнообразных задач, изучения поведения систем и принятия обоснованных решений на основе данных.
Математическая модель: сущность и необходимость

Одной из основных задач математического моделирования является построение математической модели, которая позволяет наиболее точно описать и предсказать реальные явления или события. Математическая модель позволяет сформулировать и проверить различные гипотезы, а также провести эксперименты в виртуальной среде.
Математическая модель может использоваться для решения различных задач, например, оптимизации процессов, прогнозирования поведения системы, принятия решений и других. Она позволяет анализировать и изучать различные аспекты системы, например, масштабы, структуру, параметры и динамику.
Важно отметить, что математическая модель необходима для того, чтобы избежать неконтролируемого и неструктурированного подхода к решению задачи. Она помогает систематизировать информацию, сформулировать предположения и законы, а также провести анализ и синтез различных аспектов и компонентов системы или процесса.
Примером математической модели может быть модель движения тела под действием силы тяжести. В данном случае, математическая модель может использовать законы Ньютона и другие математические понятия для описания и предсказания движения тела. Такая модель может быть использована для решения практических задач, таких как расчет траектории полета снаряда или определение времени падения объекта с заданной высоты.
Таким образом, математическая модель является мощным инструментом для анализа и решения сложных задач. Она позволяет получить новые знания о системе или процессе, а также предсказывать и оптимизировать их поведение в различных условиях. При этом, правильное построение математической модели требует глубокого понимания основных принципов и понятий математики, а также аккуратного анализа и интерпретации полученных результатов.
Классификация задач и примеры моделей
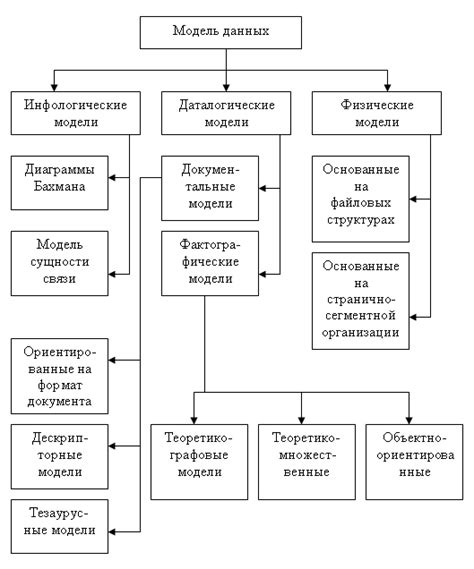
Математические модели могут быть использованы для решения различных задач, от простых и линейных до сложных и нелинейных. Предлагаемая классификация задач основана на характеристиках и типах моделей, которые могут быть применены для их решения. Вот несколько примеров классов задач и соответствующих им моделей:
Оптимизационные задачи:
Математические модели, используемые для решения оптимизационных задач, позволяют найти наилучшее решение из возможных вариантов. Примеры таких задач включают линейное программирование, задачи на сетевой анализ, задачи динамического программирования и задачи комбинаторной оптимизации.
Прогнозирование задач:
Математические модели, используемые для прогнозирования, позволяют предсказывать будущие значения на основе имеющихся данных. Примеры таких задач включают временные ряды, регрессионный анализ и методы машинного обучения, такие как нейронные сети и алгоритмы класcификации и регрессии.
Динамические задачи:
Математические модели, используемые для решения динамических задач, учитывают изменение переменных во времени. Примеры таких задач включают дифференциальные уравнения, системы дифференциальных уравнений, задачи оптимального управления и задачи транспортных потоков.
Статистические задачи:
Симуляционные задачи:
Математические модели, используемые для симуляции процессов и систем, позволяют изучать и предсказывать их поведение при различных условиях. Примеры таких задач включают моделирование случайных процессов, моделирование систем массового обслуживания и моделирование физических систем.
Каждый класс задач требует своего рода моделирования и математических инструментов для решения. Выбор правильной математической модели является ключевым шагом в решении задачи и позволяет получить точные и надежные результаты.
Определение целевых параметров и выбор модели
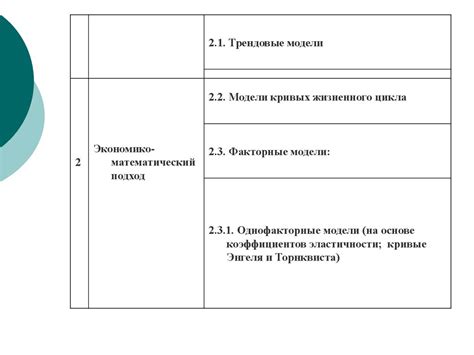
Выбор модели зависит от характеристик задачи, доступных данных и предполагаемых условий. Математическая модель должна быть адекватной и соответствовать реальным явлениям, которые она описывает. Она должна быть гибкой и удобной для решения и анализа.
- Линейные модели - описывают линейные зависимости между переменными. Они хорошо подходят для задач с линейно изменяющимися параметрами и простыми структурами.
- Нелинейные модели - описывают нелинейные зависимости между переменными. Они позволяют более гибко описывать сложные процессы и взаимодействия.
- Статистические модели - используются для анализа статистических данных и определения вероятностей различных событий.
- Оптимизационные модели - используются для поиска оптимальных решений и оптимальных значений параметров.
Выбор модели также зависит от доступных данных. Если данных мало или их качество низкое, то выбор модели может быть ограничен. В таких случаях можно использовать методы, которые позволяют оценить и улучшить качество данных, например, методы обработки и анализа данных.
Итак, определение целевых параметров и выбор модели - неотъемлемые части процесса построения математической модели задачи. Они определяются целью решения задачи, доступными данными и предполагаемыми условиями. Выбор адекватной и удобной модели играет важную роль в успешном решении задачи и получении точных и полезных результатов.



