Треугольник – это геометрическая фигура, состоящая из трех сторон и трех углов. Один из основных элементов треугольника – это его углы, которые могут быть прилежащими к его сторонам. Такие углы называются прилежащими или смежными.
Прилежащие углы прилегают к сторонам треугольника, таким образом, что каждый из них образуется парой с одной из сторон. Например, в треугольнике ABC угол А является прилежащим к сторонам AB и AC, угол В – прилежащим к сторонам AB и BC, а угол C – прилежащим к сторонам AC и BC.
Принято обозначать прилежащие углы буквами, используя рядом соответствующую заглавную букву треугольника. Например, если треугольник ABC, то угол A прилежащий к сторонам AB и AC обозначается как ∠BAC.
Знание прилежащих углов является важным для решения геометрических задач и вычисления известных величин треугольника. Зная прилежащие углы, можно определить другие углы треугольника, используя свойства геометрических фигур и треугольников, такие как сумма углов треугольника, теоремы о равенстве углов и теоремы о пропорциональности сторон.
Определение треугольника
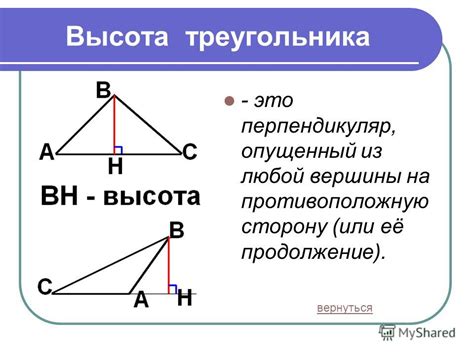
У треугольника есть несколько ключевых свойств:
1. Треугольник имеет три стороны, которые соединяют три точки в плоскости.
2. Три стороны треугольника могут быть различной длины и могут принимать любые значения, но их сумма всегда должна быть больше, чем длина любой из сторон. Это называется неравенством треугольника.
3. Треугольник имеет три угла, обозначенных обычно как A, B и C.
4. Сумма углов треугольника всегда равна 180 градусам. Поэтому прилежащие углы треугольника, то есть углы, которые лежат рядом с каждой стороной треугольника, в сумме также равны 180 градусам.
Треугольники могут быть разделены на различные типы на основе их сторон и углов. Некоторые из наиболее распространенных типов треугольников включают равносторонний треугольник, равнобедренный треугольник и прямоугольный треугольник.
Стороны треугольника
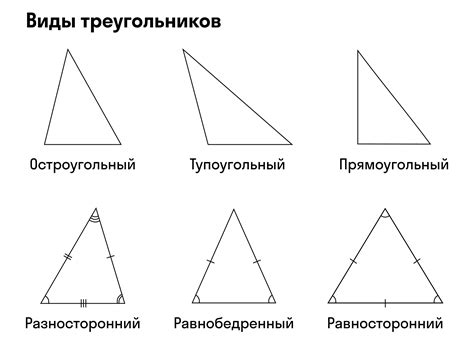
Стороны треугольника могут быть различной длины. Обозначают их обычно буквами a, b и c. Сторона a соединяет вершины A и B, сторона b - вершины B и C, а сторона c - вершины C и A.
У треугольника есть несколько важных свойств, связанных со сторонами:
1. Сумма длин любых двух сторон треугольника всегда больше длины третьей стороны. Данное свойство называется неравенством треугольника и является одним из основных критериев существования треугольника.
2. Равнобедренный треугольник имеет две равные стороны. Такой треугольник может быть также равносторонним, если все его стороны равны.
3. Разносторонний треугольник - это треугольник, у которого все три стороны различной длины.
Изучение сторон треугольника помогает определить его форму, проводить вычисления и анализировать другие характеристики этой геометрической фигуры.
Углы треугольника
Углы прилежащие к сторонам треугольника - это углы, расположенные у основания треугольника и имеющие общую сторону с этим основанием. В каждом треугольнике есть три пары углов, прилежащих к каждой из трех сторон.
Сумма углов треугольника всегда равняется 180 градусам.
Это значит, что сумма всех углов прилежащих к каждой из трех сторон также равна 180 градусам.
Таким образом, если известны два угла прилежащих к одной из сторон треугольника, то третий угол можно вычислить, вычитая сумму известных углов от 180 градусов.
Знание углов прилежащих к сторонам треугольника позволяет решать множество геометрических задач, а также использовать различные теоремы и свойства треугольников.
Понятие прилежащих углов

Прилежащие углы обладают следующим свойством: сумма мер двух прилежащих углов всегда равна мере третьего угла треугольника. Если в треугольнике углы A и B являются прилежащими углами к стороне c, то сумма мер углов A и B будет равна мере угла C.
Знание понятия прилежащих углов помогает в решении различных задач по геометрии. Оно позволяет установить связь между углами и сторонами треугольника, а также использовать геометрические свойства для вычислений и нахождения неизвестных величин.
Пример:
Рассмотрим треугольник ABC, в котором углы А и В являются прилежащими углами к стороне С. Пусть мера угла А равна 40°, а мера угла В равна 60°. Тогда, сумма мер углов А и В будет равна мере угла С. Следовательно:
40° + 60° = 100°.
Таким образом, мера угла С равна 100°.
Знание понятия прилежащих углов помогает нам установить связи между углами треугольника и решить задачу на нахождение меры угла С, используя известные меры углов А и В.
Значение углов прилежащих к сторонам треугольника

В треугольнике каждый угол имеет своё значение и взаимосвязь с другими углами и сторонами. Углы, прилегающие к сторонам треугольника, также имеют свое значение и влияют на его свойства и связи.
Углы, прилежащие к одной и той же стороне треугольника, называются смежными углами. Смежные углы могут быть как прилежащими, так и неприлежащими углами к данной стороне.
| Сторона треугольника | Прилежащий угол | Неприлежащий угол |
|---|---|---|
| AB | ∠BAC | ∠ABC |
| BC | ∠ACB | ∠ABC |
| AC | ∠CAB | ∠ACB |
Значение смежных углов зависит от свойств треугольника. Например, для прямоугольного треугольника смежные углы, прилежащие к гипотенузе, являются смежными дополнительными углами, сумма которых равна 90°. Для равностороннего треугольника все смежные углы равны между собой и составляют по 60°.
Изучение свойств углов прилежащих к сторонам треугольника помогает понять его геометрические особенности и использовать их для решения задач по геометрии.
Важность изучения прилежащих углов

Знание прилежащих углов позволяет решать разнообразные задачи, например:
- Расчет неизвестных углов и сторон: Зная значения прилежащих углов, можно вычислить неизвестные углы и стороны треугольника с использованием соответствующих геометрических формул. Это позволяет нам проверить, является ли треугольник прямоугольным, равнобедренным или равносторонним.
- Нахождение площади треугольника: Площадь треугольника можно вычислить, зная длину одной из сторон и прилежащий к ней угол. Для этого нужно использовать формулу площади треугольника, которая основана на полупериметре и радиусе описанной окружности.
Прилежащие углы также могут помочь нам понять взаимосвязь между углами и сторонами треугольника. Например, если две стороны треугольника прилегают к одному углу, то они могут быть параллельными или перпендикулярными. Это знание позволяет нам легче решать задачи и строить разнообразные геометрические фигуры.
Таким образом, изучение прилежащих углов является важной частью изучения геометрии и дает нам больше возможностей для решения задач и строительства разнообразных геометрических фигур.
Задачи на нахождение прилежащих углов
Рассмотрим несколько задач на нахождение прилежащих углов:
- Задача №1: В треугольнике ABC угол A равен 45 градусов, а угол B равен 60 градусов. Найдите значение угла C.
- Задача №2: В треугольнике DEF угол D равен 80 градусов, а угол E равен 30 градусов. Найдите значение угла F.
- Задача №3: В треугольнике XYZ угол X равен 90 градусов, а угол Y равен 45 градусов. Найдите значение угла Z.
Решение задач связанных с прилежащими углами треугольника основано на свойствах геометрических фигур, а также на знании суммы углов в треугольнике (сумма всех углов равна 180 градусов).
Для решения задачи №1 мы можем воспользоваться свойством суммы углов в треугольнике: угол C = 180 - угол A - угол B. Подставив значения, получим угол C = 180 - 45 - 60 = 75 градусов.
Аналогично для задачи №2 можем использовать свойство суммы углов в треугольнике: угол F = 180 - угол D - угол E. Подставив значения, получим угол F = 180 - 80 - 30 = 70 градусов.
Задача №3 уже несколько сложнее, так как известен только один угол и прямой угол. Однако, мы можем воспользоваться свойством суммы углов в треугольнике и свойствами прямого угла. Так как угол Y равен 45 градусов, а угол X равен 90 градусов, то угол Z = 180 - угол X - угол Y = 180 - 90 - 45 = 45 градусов.
Таким образом, решая задачи на нахождение прилежащих углов, мы применяем свойства геометрических фигур и используем знания о сумме углов в треугольнике.
Практическое применение прилежащих углов
Понимание понятия "прилежащие углы" в треугольнике имеет ряд практических применений, которые могут помочь в решении различных задач связанных с геометрией. Рассмотрим некоторые из них.
1. Определение третьего угла треугольника: зная два прилежащих угла можно вычислить третий угол треугольника, используя тот факт, что сумма углов треугольника равна 180 градусов.
2. Определение типа треугольника: с помощью прилежащих углов можно определить тип треугольника - остроугольный, тупоугольный или прямоугольный. Например, если один из прилежащих углов равен 90 градусов, то треугольник является прямоугольным.
3. Определение соотношения сторон: прилежащие углы могут помочь определить соотношение сторон треугольника. Например, если два прилежащих угла треугольника равны, то их противоположные стороны равны.
| Прилежащие углы | Тип треугольника | Соотношение сторон |
|---|---|---|
| Остроугольные | Остроугольный | Разные стороны |
| Тупоугольные | Тупоугольный | Разные стороны |
| Прямоугольные | Прямоугольный | Зависит от длин сторон |
Из приведенной выше таблицы можно видеть, что прилежащие углы важны для определения свойств треугольника и вычисления различных параметров.
Таким образом, знание прилежащих углов в треугольнике может быть полезным в различных ситуациях, связанных с геометрией, и помочь в решении задач, связанных с треугольниками и их свойствами.



