Нули и полюса передаточной функции - это понятия, важные для теории систем и сигналов. Они помогают описывать поведение системы при передаче сигнала от входа к выходу. Нули и полюса показывают, какие значения частоты могут вызывать изменения в передаче сигнала, а также как эти изменения происходят.
Нуль - это частота, при которой передаточная функция обращается в ноль. Он представляет собой особую точку на комплексной плоскости и указывает на то, что в этой точке входной сигнал будет полностью подавлен или нейтрализован. Нули позволяют определить, какие частоты блокируются или проходят через систему.
Полюс - это частота, при которой передаточная функция обращается в бесконечность. Он также представляет собой точку на комплексной плоскости и указывает на то, что в этой точке система неустойчива и создает резкое возрастание или убывание передачи сигнала. Полюса позволяют определить, насколько быстро система реагирует на входные сигналы различных частот.
Определение и основные понятия
Нули передаточной функции - это значения комплексных переменных, при которых передаточная функция обращается в ноль. Они представляют собой такие значения частоты или времени, при которых выходной сигнал системы обнуляется. Нули могут оказывать существенное влияние на стабильность и производительность системы управления.
Полюса передаточной функции - это значения комплексных переменных, при которых передаточная функция стремится к бесконечности или имеет разрыв. Они указывают на такие значения частоты или времени, при которых система становится неустойчивой или имеет скачок в выходном сигнале. Полюса также определяют динамическую характеристику системы и ее способность откликаться на внешние воздействия.
Знание о нулях и полюсах передаточной функции позволяет анализировать и проектировать системы управления, оптимизировать их параметры и предсказывать их характеристики. Понимание этих понятий позволяет инженерам и специалистам в области управления создавать более стабильные, эффективные и надежные системы управления, что имеет огромное значение в различных отраслях техники и технологий.
Нули и их значение в передаточной функции
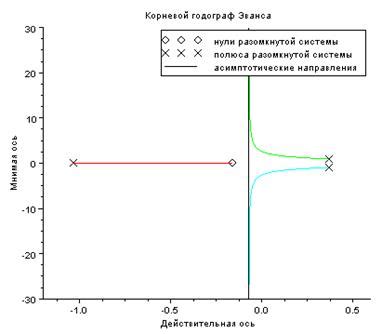
Значение нулей в передаточной функции имеет важное физическое и инженерное значение. Нули размещаются на плоскости комплексного аргумента и могут быть расположены внутри или снаружи единичного круга. Также нули могут быть расположены на вещественной оси.
Присутствие нулей в передаточной функции позволяет учитывать влияние физических и инженерных факторов на систему. Например, нули могут указывать на возможность исключения некоторых входных воздействий, что является важным в задачах фильтрации и подавления помех.
Значение нулей также может быть использовано для определения стабильности системы. Если все нули передаточной функции лежат в левой полуплоскости комплексной плоскости, то система будет устойчивой.
Влияние нулей на передаточную функцию может быть проанализировано с помощью диаграмм Боде и Найквиста. Эти диаграммы позволяют определить, как нули влияют на амплитудную и фазовую характеристики передаточной функции.
В целом, нули являются важным инструментом при анализе и проектировании систем управления. Понимание и использование концепции нулей помогает инженерам более точно и эффективно моделировать и управлять различными системами.
Полюса и их влияние на передаточную функцию
Передаточная функция системы определяет связь между входным и выходным сигналами. Она имеет вид:
G(s) = N(s) / D(s),
где G(s) - передаточная функция, N(s) - числитель, D(s) - знаменатель. Полюса определяются корнями знаменателя передаточной функции.
Каждый полюс может иметь различные значения, которые определяются характеристиками системы. Влияние полюсов на передаточную функцию состоит в следующем:
- Чем ближе полюс к мнимой оси, тем более гибкая система. Данное поведение связано с резонансами и колебаниями.
- Полюс на мнимой оси является гармоническим полюсом. Он описывает систему с гармоническим колебанием, например, при наличии незатухающих синусоидальных колебаний.
- Полюс со значением вещественной части меньше нуля определяет устойчивую систему. Устойчивая система стремится к нулю входного сигнала.
- Полюс со значением вещественной части больше нуля определяет неустойчивую систему. Неустойчивая система будет стремиться к бесконечности входного сигнала.
Таким образом, знание полюсов передаточной функции позволяет провести анализ и определить характеристики системы. Например, устойчива ли она, имеет ли нежелательные колебания или резонансы.
Виды нулей и полюсов
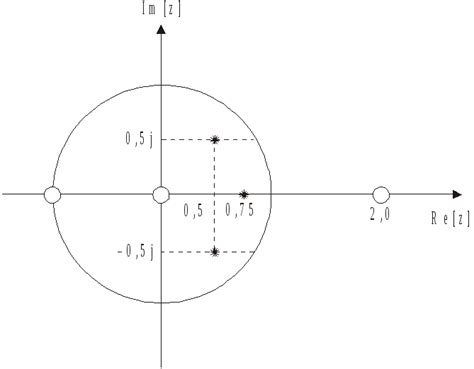
Нули передаточной функции - это значения, при которых функция обращается в ноль. Они определяют места, где передаточная функция имеет нулевое значение и сигналы не передаются. В зависимости от расположения нулей можно выделить несколько видов:
- Реальные нули - когда нули функции находятся на вещественной оси, то есть представлены действительными числами. Реальные нули говорят о существовании точек, где передача сигналов полностью блокируется.
- Комплексные нули - когда нули функции находятся в комплексной области, то есть представлены комплексными числами. Комплексные нули говорят о существовании частот, на которых передаточная функция будет обращаться в ноль.
- Нули на бесконечности - когда передаточная функция обращается в ноль на бесконечности. Это значит, что на бесконечности передача сигналов полностью прекращается.
Полюса передаточной функции - это значения, при которых функция становится бесконечной или расходится. Полюсы определяют места, где передаточная функция имеет бесконечное значение и сигналы усиливаются. В зависимости от расположения полюсов можно выделить несколько видов:
- Реальные полюса - когда полюсы функции находятся на вещественной оси, то есть представлены действительными числами. Реальные полюса говорят о существовании точек, где сигналы усиливаются.
- Комплексные полюса - когда полюсы функции находятся в комплексной области, то есть представлены комплексными числами. Комплексные полюса говорят о существовании частот, на которых сигналы будут усиливаться.
- Полюса на бесконечности - когда передаточная функция становится бесконечной на бесконечности. Это значит, что на бесконечности сигналы неограниченно усиливаются.
Примеры нулей и полюсов в передаточных функциях
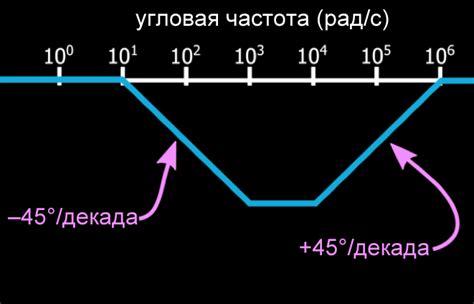
Рассмотрим несколько примеров нулей и полюсов в передаточных функциях:
- Передаточная функция вида H(z) = (z - z0), где z0 - ноль функции. В этом случае, ноль находится в точке z = z0 и соответствует точке пересечения функции с осью z.
- Передаточная функция вида H(s) = 1 / (s - p0), где p0 - полюс функции. В этом случае, полюс находится в точке s = p0 и соответствует точке пересечения функции с осью s.
- Передаточная функция вида H(s) = (s - p1)(s - p2), где p1 и p2 - полюсы функции. В этом случае, полюсы находятся в точках s = p1 и s = p2, и соответствуют точкам пересечения функции с осью s.
- Передаточная функция вида H(s) = (s - z1)(s - z2) / (s - p1)(s - p2), где z1 и z2 - нули функции, а p1 и p2 - полюсы функции. В этом случае, нули находятся в точках s = z1 и s = z2, и соответствуют точкам пересечения функции с осью s, а полюсы находятся в точках s = p1 и s = p2.
Примеры нулей и полюсов в передаточных функциях позволяют проиллюстрировать, как эти элементы влияют на форму функции и ее поведение в различных точках частотного диапазона.
Устранение нулей и полюсов
Нули передаточной функции определяют места входов, где выход имеет нулевое значение. Единичный ноль означает, что сигнал на этом входе не оказывает влияния на выход системы. Множественные нули могут указывать на наличие перепадов в усилении или фазовых сдвигов в системе. В случае, если нули находятся в правой полуплоскости комплексной плоскости, система может стать неустойчивой.
Полюса передаточной функции определяют места, где передача сигнала системой бесконечно усиливается или затухает. Есть два типа полюсов: действительные полюса и комплексные полюса. Действительные полюса имеют влияние на устойчивость и динамику системы. Комплексные полюса указывают на наличие колебательных характеристик в системе.
Устранение нулей и полюсов может быть необходимо для достижения заданных характеристик системы управления, таких как стабильность, точность, скорость реакции и др. Это может быть достигнуто путем изменения передаточной функции, добавления или удаления нулей и полюсов.
Важно учитывать, что устранение нулей и полюсов может привести к изменению динамики и устойчивости системы управления. Поэтому, при проектировании системы необходимо тщательно анализировать влияние каждого изменения передаточной функции.
Полюсно-нулевые диаграммы передаточных функций

Полюсно-нулевая диаграмма передаточной функции представляет собой графическое представление положения нулей и полюсов передаточной функции в комплексной плоскости. Эта диаграмма позволяет проанализировать основные характеристики системы и определить ее стабильность и устойчивость.
Нулями передаточной функции являются решения уравнения передаточной функции, при которых числитель функции равен нулю. Полюсами передаточной функции являются решения уравнения передаточной функции, при которых знаменатель функции равен нулю. Положение нулей и полюсов определяет форму и свойства передаточной функции.
На полюсно-нулевых диаграммах передаточных функций нули и полюса обозначаются точками, расположенными на комплексной плоскости. Нули обозначаются кружками, а полюса - крестиками. Расположение этих точек позволяет определить степень устойчивости системы и ее поведение.
Полюсно-нулевые диаграммы передаточных функций часто используются при проектировании и анализе систем управления и фильтрации. Они позволяют определить, как система будет испытывать колебания, реагировать на входные сигналы и подавлять шум или помехи.
Анализ полюсно-нулевых диаграмм передаточных функций позволяет инженерам и научным работникам предварительно оценить свойства и производительность системы, прежде чем строить реальные модели и проводить эксперименты. Это экономит время и ресурсы, а также позволяет предотвратить возможные проблемы и улучшить результаты проектирования.
| Символ | Значение |
|---|---|
| О | Нуль |
| X | Полюс |
Свойства нулей и полюсов в системах управления
Нули передаточной функции являются корнями ее числителя. Они определяют, при каком значении частоты передаточная функция обращается в ноль. Нули влияют на форму графика амплитудно-частотной и фазово-частотной характеристики. Если передаточная функция имеет нули на мнимой оси, то система будет обладать резонансами или позволит получить бесконечное усиление выходного сигнала.
Полюса передаточной функции являются корнями ее знаменателя. Они определяют, при каком значении частоты передаточная функция обращается в бесконечность. Полюса также влияют на форму графика амплитудно-частотной и фазово-частотной характеристики. Если все полюса находятся в левой полуплоскости комплексной плоскости, то система является устойчивой.
Система управления может быть устойчивой только если все ее полюса находятся в левой полуплоскости комплексной плоскости, иначе она будет неустойчивой или гранично устойчивой. Нули и полюса могут быть как вещественными, так и комплексными числами.
Анализ и понимание свойств нулей и полюсов передаточной функции позволяют инженерам проектировать системы управления с нужными характеристиками. Они могут использовать различные методы и подходы, такие как перемещение нулей и полюсов, чтобы добиться желаемого поведения системы.
Расчет нулей и полюсов передаточной функции
Нули передаточной функции представляют собой значения частоты, при которых знаменатель функции обращается в ноль, т.е. выходной сигнал становится равным нулю. Нули указывают на особые точки, в которых передаточная функция может изменять свое поведение.
Полюса передаточной функции представляют собой значения частоты, при которых числитель функции обращается в ноль, т.е. выходной сигнал стремится к бесконечности. Полюса указывают на особые точки, в которых передаточная функция может иметь разрывы или колебательное поведение.
Расчет нулей и полюсов передаточной функции может быть выполнен с использованием различных методов, включая алгоритм Найквиста и методы кругов и прямых. В общем случае, это требует решения алгебраического уравнения, полученного из передаточной функции.
После расчета нулей и полюсов, можно провести анализ стабильности и устойчивости системы управления. Например, если все полюса передаточной функции лежат в левой полуплоскости комплексной плоскости, то система будет устойчивой. Если есть полюса, лежащие в правой полуплоскости, то система может быть неустойчивой.
| Символ | Обозначение | Описание |
|---|---|---|
| Ноль | z | Точка, при которой передаточная функция обращается в ноль |
| Полюс | p | Точка, при которой передаточная функция стремится к бесконечности |



