Черточки на треугольниках – это особые отметки или линии, которые проводятся на сторонах или углах треугольников для обозначения определенных свойств и характеристик. Геометрия, как наука о пространственных фигурах и их свойствах, широко использует черточки на треугольниках для облегчения анализа и решения задач.
Зачем же нужны эти черточки? Они помогают установить соотношения между сторонами и углами треугольников, которые могут быть важными для решения задач геометрии. Через черточки можно обозначить равные длины сторон, равные углы, отрезки, составляющие определенные пропорции и многое другое.
Различные черточки на треугольниках имеют свои названия и значение. Например, одна из самых часто используемых черточек – черта над стороной, которая указывает на ее равенство с другой стороной. Это свойство треугольников называется равенством сторон по названию этой черты.
Черточки на треугольниках в геометрии: определение и значение
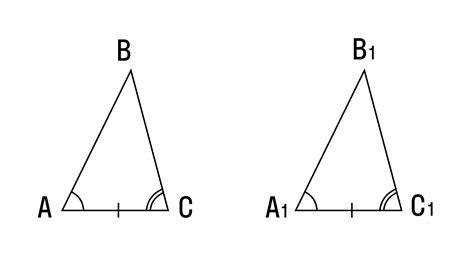
Черточки являются важными элементами треугольника, их длина и расположение влияют на его свойства и характеристики.
Длина черточек определена следующим образом: каждая черточка делит соответствующую сторону треугольника пополам. То есть, если AB – одна из сторон треугольника, а M – средняя точка стороны AB, то длина черточки AM будет равна длине черточки MB.
Черточки играют важную роль в геометрии треугольников, они обладают несколькими уникальными свойствами. Например, черточки треугольника пересекаются в одной точке, которая называется центром тяжести. Эта точка делит каждую черточку в отношении 2:1, то есть от центра тяжести до вершины черточки и от центра тяжести до средней точки противоположной стороны черточки будут относиться как 2:1.
Также, черточки определяют шесть треугольников внутри исходного треугольника. Эти треугольники называются медианами треугольника и имеют схожие свойства. Например, длина медианы будет меньше длины соответствующей стороны и больше половины периметра треугольника.
Черточки на треугольнике имеют ценность в геометрии, так как они позволяют использовать особенности и свойства треугольников в различных расчетах и задачах. Знание черточек и их свойств позволяет углубить понимание структуры и характеристик треугольников, а также использовать их в решении более сложных задач геометрии.
Таким образом, черточки на треугольниках являются важными элементами, которые определяют не только структуру треугольника, но и его свойства. Знание черточек и их свойств позволяет проводить более глубокий анализ и решение задач в геометрии треугольников.
Определение черточек на треугольнике
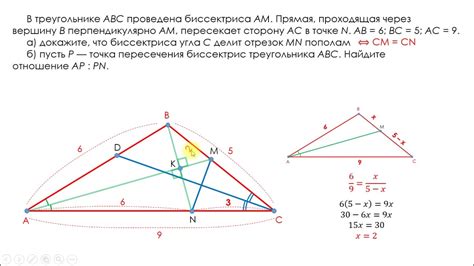
Медиана, проведенная из вершины треугольника, делит противоположную сторону на две равные части. Все три черточки пересекаются в одной точке, называемой центром тяжести или барицентром треугольника.
Черточки на треугольнике имеют следующие особенности:
- Длина черточек соответствует половине длины соответствующих сторон треугольника.
- Центр тяжести треугольника является точкой пересечения черточек.
- Черточки делят треугольник на шесть равных треугольников.
- Черточки служат опорой для построения других конструкций в геометрии, таких как окружности и другие фигуры.
Черточки на треугольнике имеют важное значение в геометрии и широко используются для анализа и вычислений свойств треугольников. Они помогают понять и визуализировать различные аспекты треугольников и их связей с другими геометрическими фигурами.
Значение черточек в геометрии
Черточки на треугольниках в геометрии играют важную роль и используются для обозначения различных элементов треугольника. Они помогают нам лучше понять и изучить свойства и характеристики треугольников.
Также черточки используются для обозначения параллельных сторон треугольника. Если в треугольнике две стороны параллельны между собой, то на них рисуют две черточки. Это помогает нам определить свойства треугольников с параллельными сторонами, например, параллелограммы или ромбы.
Черточки также могут указывать на перпендикулярные стороны треугольника. Если сторона треугольника перпендикулярна к одному из углов треугольника, на нее рисуют перпендикулярную черточку. Это помогает нам определить свойства прямоугольных треугольников и работать с их углами и сторонами.
Значение черточек в геометрии не стоит недооценивать. Их наличие и расположение на треугольниках помогает нам определить свойства и особенности каждой фигуры, а также делает геометрические рассуждения более понятными и удобными.
Как образуются черточки на треугольниках
Черточки на треугольниках образуются в результате пересечения секущих линий с треугольной фигурой. Они представляют собой отрезки, которые соединяют две стороны треугольника или сторону с вершиной.
Существует три типа черточек на треугольниках:
- Медианы: черточки, которые соединяют каждую вершину треугольника с серединой противоположной стороны. Таким образом, треугольник имеет три медианы, которые пересекаются в точке, называемой центром тяжести.
- Биссектрисы: черточки, которые делят углы треугольника пополам. Каждый угол имеет две биссектрисы, которые пересекаются в точке, называемой центром вписанной окружности.
- Высоты: черточки, которые опущены из вершин треугольника на противоположные стороны. Таким образом, треугольник имеет три высоты, которые пересекаются в точке, называемой ортоцентром.
Черточки на треугольниках обладают рядом интересных свойств и играют важную роль в геометрии. Они помогают определить центры и окружности, а также находить различные углы и отношения между сторонами треугольника.
Свойства черточек на треугольниках
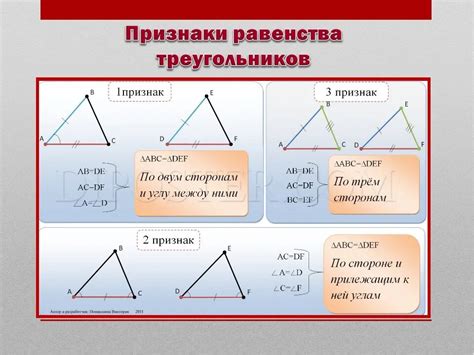
Самая известная черточка на треугольнике - это медиана. Медиана - это отрезок, который соединяет вершину треугольника с серединой противоположной стороны. Очень важно отметить, что в треугольнике всегда существуют три медианы, которые пересекаются в одной точке, называемой центром масс треугольника.
Вторая черточка, которую мы часто используем, - это высота. Высота - это отрезок, опущенный из вершины треугольника на противоположную сторону или его продолжение. Важно отметить, что в треугольнике всегда есть три высоты, и они пересекаются в одной точке, называемой ортоцентром.
Третья черточка - это биссектриса. Биссектриса - это отрезок, который делит угол треугольника пополам и проходит через вершину смежной стороны. В треугольнике всегда существуют три биссектрисы, и они пересекаются в одной точке, называемой центром вневписанной окружности треугольника.
Использование черточек на треугольниках позволяет нам легко находить различные свойства треугольников и решать геометрические задачи. Они помогают нам определить центры треугольников и связанные с ними особенности. Поэтому понимание и использование черточек на треугольниках является важным навыком для изучения геометрии.
Способы измерения черточек на треугольниках

- Использование линейки: Для измерения длины черточки на треугольнике можно использовать обычную линейку. Проведите линейку вдоль черточки и определите ее длину, записывая результат.
- Использование угломера: Если черточка на треугольнике является углом, вы можете использовать угломер. Приложите одну сторону угломера к одному из концов черточки и определите угол, записывая результат.
- Использование гониометра: Если черточка на треугольнике является углом, вы можете использовать гониометр. Поставьте гониометр на черточку, чтобы определить угол с помощью шкалы гониометра.
- Использование формул: В некоторых случаях черточки на треугольниках могут быть измерены с использованием определенных математических формул. Это может включать расчет длины черточки с использованием теоремы Пифагора или расчет угла с использованием тригонометрических функций.
- Использование компьютерных программ: Современные компьютерные программы для геометрии могут предоставить возможность измерять черточки на треугольниках. Это может быть полезным, особенно для сложных треугольников или когда требуется высокая точность измерений.
Способ измерения черточек на треугольниках выбирается в зависимости от их характера и доступных инструментов. Важно помнить, что точность измерений может быть ограничена инструментами и ограничениями метода измерения.
Применение черточек в решении геометрических задач
Черточки на треугольниках в геометрии имеют много применений и часто используются при решении различных геометрических задач. Они помогают установить отношения между сторонами и углами треугольников, а также выявить специальные свойства треугольников.
Одним из основных способов использования черточек на треугольнике является построение медиан - линий, соединяющих вершины треугольника с серединами противолежащих сторон. Эти линии делят каждую медиану на две равные части и пересекаются в точке, называемой центром тяжести треугольника. Черточки, построенные через центр тяжести треугольника, также делят его на шесть равных треугольников, что может быть полезно при решении различных задач на равенство площадей.
Еще одним способом использования черточек является построение биссектрис - линий, делящих углы треугольника на две равные части. Биссектрисы также пересекаются в одной точке, называемой центром вписанной окружности треугольника. Через этот центр вписанной окружности также можно провести черточку, перпендикулярную одной из сторон треугольника, которая будет проходить через точку касания вписанной окружности со стороной треугольника. Это свойство может быть использовано при решении задач на равенство отрезков и углов.
Черточки на треугольнике также помогают установить соотношения между сторонами и углами треугольника. Например, через вершину треугольника можно провести черточку, перпендикулярную одной из сторон, и таким образом разделить эту сторону на две части, пропорциональные другим двум сторонам треугольника. Это соотношение известно как теорема о разделении сторон треугольника.
Примеры использования черточек на треугольниках
1. Разделение сторон треугольника на равные части:
Черточки могут быть использованы для разделения сторон треугольника на равные части. Это позволяет упростить решение задач, связанных с построением или измерением треугольников.
2. Определение углов и сторон:
Черточки помогают определить углы и стороны треугольника, что очень полезно при изучении его свойств и применении в различных геометрических задачах. Они могут использоваться для угловой и линейной измерений и помогают ясно обозначить различные элементы треугольника.
3. Упрощение построения графиков и диаграмм:
Дополнительные черточки на границах треугольников могут использоваться для построения графиков и диаграмм, где каждая черточка представляет определенное значение. Это удобно для визуализации данных и сравнения различных значений на графике или диаграмме.
4. Помощь в проведении параллельных и перпендикулярных линий:
Черточки на треугольниках можно использовать для проведения параллельных и перпендикулярных линий. Они могут служить в качестве ориентира при построении и помогают наглядно представить понятия параллельности и перпендикулярности.
5. Упрощение изучения и понимания геометрических концепций:
Черточки могут быть использованы для упрощения изучения и понимания различных геометрических концепций, таких как медианы, биссектрисы, высоты и теоремы, связанные с треугольниками. Они помогают визуализировать эти концепции и сделать их более понятными и доступными для обучения.
Специфика использования черточек в разных типах треугольников

В геометрии существует несколько различных типов треугольников, в которых черточки могут использоваться с разными целями и иметь различные значения. Рассмотрим особенности использования черточек в трех основных типах треугольников: прямоугольных, равнобедренных и разносторонних.
1. Прямоугольные треугольники:
| Черточки | Значение |
|---|---|
| Медиана из вершины прямого угла | Делит прямой угол на два равных угла |
| Высота из вершины прямого угла | Является перпендикулярной к гипотенузе и проходит через вершину прямого угла |
| Биссектриса прямого угла | Делит прямой угол на два равных угла и проходит через вершину прямого угла |
2. Равнобедренные треугольники:
| Черточки | Значение |
|---|---|
| Медиана из вершины угла при основании | Делит основание на две равные части и проходит через вершину угла при основании |
| Биссектриса угла при основании | Делит угол при основании на два равных угла и проходит через вершину угла при основании |
| Высота из вершины угла при основании | Является перпендикулярной к основанию и проходит через вершину угла при основании |
3. Разносторонние треугольники:
| Черточки | Значение |
|---|---|
| Медианы | Делят стороны на равные сегменты и пересекаются в одной точке (центре тяжести) |
| Высоты | Являются перпендикулярными к сторонам и проходят через вершины треугольника |
| Биссектрисы | Делят углы на две равные части и пересекаются в одной точке (центре вписанной окружности) |
Использование черточек в треугольниках позволяет увидеть особенности и свойства каждого типа треугольника, а также помогает решать различные геометрические задачи.
Альтернативные методы обозначения сторон треугольников
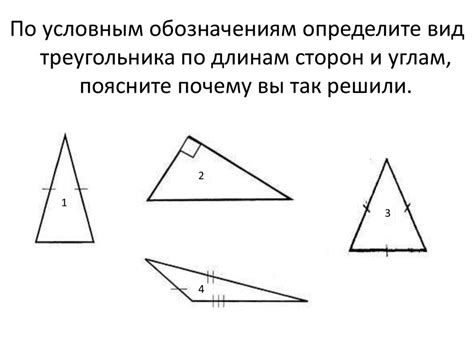
Помимо традиционной Черточки через две точки, существуют другие методы обозначения сторон треугольников. Они могут быть использованы для различных целей и могут предоставлять дополнительную информацию о сторонах.
Один из таких методов - использование буквенных обозначений сторон. Вместо черточки, стороны обозначаются буквами, например, "AB", "BC" и "CA". Такое обозначение может быть особенно полезно, когда треугольник встречается в контексте более сложной геометрической фигуры, такой как многоугольник или параллелограмм.
Другим методом является использование числовых значений для обозначения сторон треугольника. Каждая сторона может быть пронумерована, например, последовательностью чисел 1, 2 и 3. Это также может быть полезно при выполнении математических операций с треугольниками или при анализе их свойств.
В таблице ниже приведены примеры альтернативных методов обозначения сторон треугольника:
| Метод | Пример обозначения |
|---|---|
| Традиционная Черточка через две точки | AB, BC, CA |
| Буквенные обозначения сторон | a, b, c |
| Числовые обозначения сторон | 1, 2, 3 |
Выбор метода обозначения сторон треугольника зависит от контекста и целей анализа. Каждый метод имеет свои преимущества и может быть использован для более точного и удобного представления информации о треугольнике.



