Математика - это наука, которая изучает числа, формулы, структуры и пространство. Она играет важную роль в разных сферах жизни и является неотъемлемой частью нашей повседневной деятельности. Учебники, задания и уроки по математике часто содержат примеры с использованием символов и знаков. Одним из таких символов является звездочка, которая имеет свое значение в контексте математики.
Звездочка в математических примерах обычно используется для обозначения операции умножения. Она является альтернативным символом для умножения и широко применяется в разных странах, включая Россию. Например, если у нас есть пример "5 * 3", то звездочка указывает на то, что необходимо перемножить числа 5 и 3. В данном случае результат будет равен 15.
Хотя звездочка является наиболее распространенным символом для обозначения умножения в математике, некоторые учебники и преподаватели могут использовать другие символы, такие как точка "·" или крестик "x". Это особенно часто встречается в печатных изданиях, где звездочка может быть затруднительной для восприятия или красочности изображений.
Важно помнить, что звездочка может иметь различные значения в зависимости от контекста. Например, в статистике она может обозначать умножение, а в программировании - комментарий или указатель на указатель. Поэтому при изучении математики всегда важно обращать внимание на контекст и интерпретировать знаки и символы в соответствии с заданием или примером.
Звездочка в математике: объяснение и значения

В выражениях и уравнениях звездочка ставится между двумя числами или переменными, чтобы указать на операцию умножения. Например, выражение 3 * 4 означает, что число 3 умножается на число 4.
Однако, звездочка может иметь и другие значения в зависимости от контекста.
Значение звездочки в математике:
1. Умножение: Как уже упоминалось выше, в основном звездочка используется для обозначения операции умножения. Например, 5 * 2 означает умножение числа 5 на число 2.
2. Произведение векторов: В линейной алгебре звездочка может обозначать операцию векторного произведения. Это операция, которая применима только к векторам и в результате дает вектор, перпендикулярный обоим исходным векторам.
3. Указатель на комментарий: В некоторых случаях, звездочка может использоваться в комментариях в математических записях для привлечения внимания к определенным частям выражения или формулы. Она может служить для выделения объяснений или для указания на какие-то важные моменты.
4. Индикатор звездного решения: В некоторых математических задачах звездочка может обозначать особое решение, часто называемое "звездным", которое отличается от общего решения.
В зависимости от контекста и области математики, звездочка может иметь и другие значения. Важно учесть, что значение звездочки следует определять исходя из используемого математического текста или обозначений, чтобы избежать путаницы и неправильных толкований.
Звездочка в примере: отличительная особенность математических задач

Звездочка используется как знак операции умножения в различных областях математики, включая арифметику, алгебру, геометрию и т.д. В математических выражениях звездочка помогает обозначить, что два числа или выражения нужно перемножить, а не сложить или разделить.
Примеры использования звездочки в математических задачах:
| 2 * 3 = 6 | Звездочка (*) обозначает умножение двух чисел: 2 и 3. |
| x * y = z | Звездочка (*) обозначает умножение двух переменных: x и y, результатом будет переменная z. |
| (a + b) * c = d | Звездочка (*) обозначает умножение выражения (a + b) на число c, результатом будет число d. |
Использование звездочки в примере помогает читателю сразу понять, что речь идет о перемножении чисел или выражений. Без звездочки такая операция была бы малоотличима от сложения или деления. Поэтому звездочка является важным элементом математической нотации и помогает упростить запись и понимание математических задач.
Значение звездочки в формулах и уравнениях
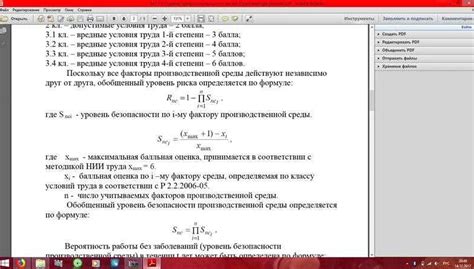
Звездочка (*) в математике имеет различное значение в контексте формул и уравнений. Рассмотрим несколько примеров:
Умножение чисел: звездочка используется для обозначения операции умножения двух чисел. Например, выражение 2 * 3 означает умножение числа 2 на число 3, что в результате дает число 6.
Перемножение переменных: в математических формулах звездочка может обозначать перемножение двух переменных. Например, если у нас есть формула a * b * c, это означает, что переменные a, b и c умножаются между собой.
Произведение чисел: звездочка может использоваться для обозначения произведения нескольких чисел. Например, выражение 2 * 3 * 4 означает произведение чисел 2, 3 и 4, что в результате дает число 24.
Производная функции: в математическом анализе звездочка может использоваться для обозначения производной функции. Например, f'(x) обозначает производную функции f(x).
Декартово произведение: в теории множеств звездочка может использоваться для обозначения декартова произведения двух множеств. Например, A*B обозначает декартово произведение множеств A и B.
Таким образом, значение звездочки в формулах и уравнениях зависит от контекста и может использоваться для обозначения умножения чисел, перемножения переменных, произведения чисел, производной функции или декартова произведения множеств.
Звездочка в математическом обозначении переменных

Звездочка (*) в математике используется для обозначения операции умножения, а также для обозначения переменных.
Когда звездочка используется в качестве операции умножения, она обозначает умножение двух чисел. Например, выражение 2 * 3 означает умножение числа 2 на число 3 и равно 6.
Кроме того, звездочка может использоваться для обозначения переменных в математических выражениях. В этом случае звездочка обычно используется как символ заполнителя или джокер. Например, выражение x * y означает произведение двух переменных x и y, где x и y могут принимать любые значения.
Использование звездочки в качестве обозначения переменных позволяет создавать универсальные формулы и уравнения, которые могут быть применены к различным значениям переменных.
Например, уравнение y = a * x + b, где a и b являются коэффициентами, а x и y являются переменными, задает линейную функцию, где значение y зависит от значения переменной x.
Таким образом, звездочка в математическом обозначении переменных представляет собой мощный инструмент для создания и изучения математических моделей и выражений.
Использование звездочки в терминах и определениях

Одно из наиболее распространенных использований звездочки в математике - обозначение операции умножения. Например, если вы видите выражение 2 * 3, оно означает, что число 2 умножается на число 3, и результатом этой операции будет число 6. В этом случае звездочка является знаком операции и разделяет множители.
Однако звездочка не всегда обозначает умножение. В некоторых случаях она может использоваться для обозначения других математических операций, таких как возведение в степень или операция модуля. Например, запись 2 * 3^2 означает, что число 2 умножается на число 3 в квадрате, что приведет к результату 18. Здесь звездочка разделяет множитель и степень.
Звездочка также может использоваться для обозначения отношения или операции поиска. Например, в статистике звездочка может обозначать значимость или статистическую значимость. Когда звездочка указывается рядом с результатом исследования или статистическим показателем, это означает, что результат является статистически значимым и отличается от случайного.
Кроме того, звездочка может иметь свое значение в определенных областях математики, таких как логика и теория множеств. Например, в логике звездочка может обозначать операцию логического "И" или "умножение" логических значений. В теории множеств звездочка может обозначать операцию декартова произведения двух множеств.
В итоге, использование звездочки в математике может быть очень многообразным и зависит от контекста. При чтении математических уравнений и примеров важно внимательно анализировать и интерпретировать значение звездочки, чтобы правильно понять смысл операции или отношения, которые она обозначает.



