Умножение и деление являются основными арифметическими операциями, с которыми мы сталкиваемся ежедневно. Они играют важную роль в нашей жизни и позволяют нам решать различные задачи. Умение правильно выполнять умножение и деление натуральных чисел является основой для понимания более сложных математических операций.
Умножение - это операция, при которой мы складываем одно и то же число несколько раз. Умножение можно представить как быстрое сложение. Например, при умножении числа 3 на число 4 мы складываем число 3 четыре раза: 3 + 3 + 3 + 3 = 12.
Деление - это операция, обратная умножению. При делении число разбивается на равные группы. Деление можно представить как нахождение ответа на вопрос: сколько раз число А содержится в числе В. Например, при делении числа 12 на число 4 мы разбиваем число 12 на 4 группы по 3 элемента в каждой: 12 / 4 = 3.
Что такое умножение и деление
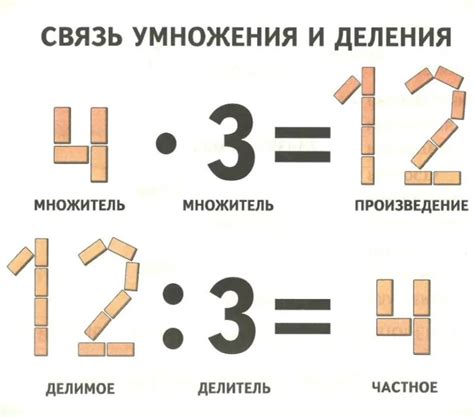
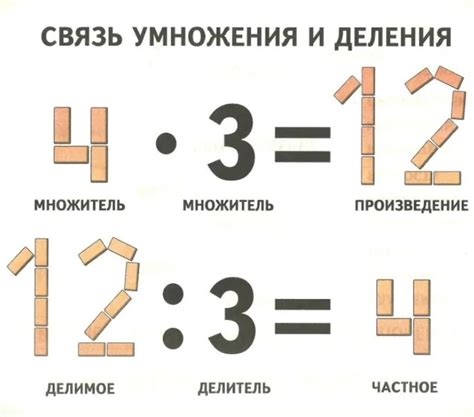
Умножение - это операция, при которой два или более числа (множители) объединяются, чтобы получить одно число (произведение). Произведение чисел равно результату умножения.
Например, если умножить 3 на 4, получится произведение 12. Это означает, что 3 умножить на 4 равно 12.
Деление - это операция, обратная умножению. Она позволяет разделить одно число (делимое) на другое число (делитель), чтобы получить результат (частное).
Например, если разделить 12 на 3, получится частное 4. Это означает, что 12 разделить на 3 равно 4.
Умножение и деление можно использовать для решения различных задач, таких как вычисление площади прямоугольника, разделение группы предметов поровну на несколько частей и многое другое.
Правила умножения и деления
Правила умножения:
- При умножении однозначного числа на любое число, результатом будет само это число.
- При умножении числа на 10, 100, 1000 и т.д. результатом будет число, в котором цифры увеличены на столько разрядов, сколько в знаменателе степени десятки.
- При умножении двузначного числа на некоторое число, сначала умножают одну цифру этого числа на число, затем другую цифру.
- При умножении многозначного числа на некоторое число, каждую его цифру умножают на это число, начиная с последней и движась к первой.
Правила деления:
- При делении числа на 10, 100, 1000 и т.д. результатом будет число, в котором цифры уменьшены на столько разрядов, сколько в знаменателе степени десятки.
- При делении двузначного числа на однозначное число, число десятков исходного числа нужно разделить на это однозначное число, затем число единиц.
- При делении двузначного числа на двузначное число, число, полученное на первом шаге деления, нужно разделить на новое двузначное число и получить остаток, который добавится к цифре единиц полученного числа.
- При делении многозначного числа на некоторое число, на первом шаге деления цифра с наибольшим разрядом делится на это число, затем прибавляется следующая цифра и вся полученная сумма делится на это число, и т.д.
Правила умножения и деления помогают справиться с математическими вычислениями и решением задач в школьной и повседневной жизни.
Примеры умножения натуральных чисел

Ниже приведены несколько примеров умножения натуральных чисел:
- Умножение чисел 2 и 3:
2 * 3 = 6
В результате умножения чисел 2 и 3 получается число 6. - Умножение чисел 5 и 4:
5 * 4 = 20
При умножении числа 5 на 4 получается число 20. - Умножение чисел 7 и 1:
7 * 1 = 7
Умножение числа 7 на 1 дает результат равный 7. - Умножение чисел 9 и 0:
9 * 0 = 0
При умножении числа 9 на 0 получается число 0.
Умножение натуральных чисел применяется во многих областях, таких как математика, физика, экономика и технические науки. Это важная операция, которая позволяет расчитывать результаты различных вычислений и моделировать процессы роста и изменения.
Как умножать числа с несколькими разрядами

В начале умножения необходимо помнить о десятичной системе счисления и правилах умножения одноразрядных чисел. Затем можно перейти к умножению чисел со множеством разрядов.
Чтобы умножить два числа с несколькими разрядами, сначала перемножьте каждую цифру первого числа на каждую цифру второго числа, начиная с крайнего правого разряда. Затем сложите полученные промежуточные произведения, учитывая позиции разрядов и переносы, если таковые имеются. Результат будет произведением двух чисел.
Во время умножения, выравнивайте промежуточные произведения по разрядам и положению запятой. В случае многоразрядных чисел, выравнивание поможет сохранить правильную структуру чисел в процессе умножения.
Процесс умножения может быть сложным при работе с числами большого размера, поэтому рекомендуется использовать запись умножения в столбик, чтобы упростить его выполнение.
Вот пример умножения чисел с несколькими разрядами:
256
× 32
──────
512
+ 7680
────────
8192
В этом примере мы умножаем число 256 на число 32. Перемножаем каждую цифру числа 256 на каждую цифру числа 32 и получаем промежуточные произведения: 2×32, 5×32 и 6×32. Затем складываем эти промежуточные произведения и получаем результат умножения: 8192.
Ознакомившись с правилами и примерами умножения чисел с несколькими разрядами, вы сможете успешно выполнять эту операцию и применять ее в решении различных математических задач.
Примеры деления натуральных чисел
Рассмотрим несколько примеров деления натуральных чисел:
| Делимое | Делитель | Частное |
|---|---|---|
| 12 | 3 | 4 |
| 15 | 5 | 3 |
| 24 | 8 | 3 |
В первом примере мы делим число 12 на 3 и получаем частное равное 4. Это означает, что 12 можно поделить на 3 равные группы по 4 элемента в каждой.
Во втором примере мы делим число 15 на 5 и также получаем частное равное 3. То есть число 15 можно поделить на 5 равных групп по 3 элемента в каждой.
В третьем примере мы делим число 24 на 8 и также получаем частное равное 3. Это означает, что число 24 можно поделить на 8 равных групп по 3 элемента в каждой.
Таким образом, примеры деления натуральных чисел помогают нам лучше понять и применить это математическое действие в различных ситуациях.
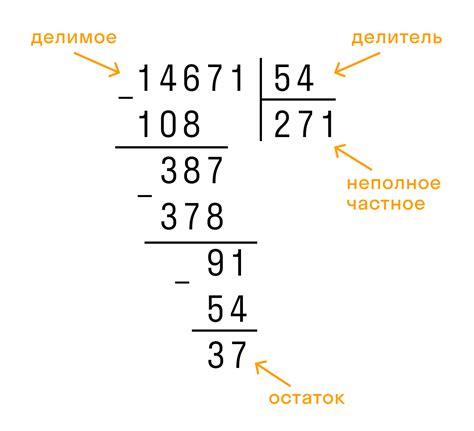
Как делить числа с несколькими разрядами

Для того чтобы выполнить деление чисел с несколькими разрядами, следуйте следующим шагам:
- Расставьте числа, которые вы делите, одно под другим, с целым числом и делителем выровненными по разрядам.
- Начинайте деление с самого левого разряда и переносите остаток от деления каждого разряда на следующий. Если остатка нет, переносите 0.
- Если число в разряде, которое вы делите, меньше делителя, перенесите следующий разряд вместе с этим разрядом.
- Вписывайте результат деления в столбик снизу вверх.
- Продолжайте деление до тех пор, пока не достигнете последнего разряда.
Важно помнить, что при делении с несколькими разрядами может потребоваться выполнить несколько итераций, чтобы корректно выполнить операцию. Также, будьте внимательны при записи результатов деления, чтобы не допустить ошибки.
Ниже приведен пример деления чисел с несколькими разрядами:
| 1 | 0 | 4 | 0 | |
| / | 2 | |||
| 0 | . | 5 | 2 | |
В данном примере, число 1040 делится на 2. Следуя шагам, мы получаем результат деления 0.52.
Теперь, когда вы понимаете методику деления чисел с несколькими разрядами, вы можете применять ее для решения более сложных математических задач и задач повседневного применения.
Полезные свойства умножения и деления

Одно из основных свойств умножения - коммутативность. Это значит, что порядок множителей не имеет значения, результат будет одинаковым. Например, 2 умножить на 3 или 3 умножить на 2 даст результат 6.
Другое полезное свойство - ассоциативность умножения. Это означает, что можно менять порядок скобок при умножении трех чисел, результат будет всегда одинаковым. Например, (2 перемножить на 3) умножить на 4 или 2 перемножить на (3 умножить на 4) даст результат 24.
Умножение имеет также свойство нейтрального элемента - число 1. Умножение любого числа на 1 дает в результате это же число. Например, 5 умножить на 1 равно 5.
Свойства деления в значительной степени связаны с умножением. Деление является обратной операцией к умножению, то есть, если результат умножения двух чисел равен третьему числу, то результат деления третьего числа на один из множителей равен второму множителю.
Деление также имеет свойство нейтрального элемента - число 1. Деление любого числа на 1 дает в результате это же число. Например, 10 делить на 1 равно 10.
Важно знать и применять эти свойства умножения и деления при выполнении арифметических операций с натуральными числами, так как они позволяют упростить вычисления и решение задач. Изучение этих свойств является основой для дальнейшего изучения математики.



