Геометрия - наука, изучающая пространственные фигуры, их свойства и взаимное расположение. В рамках геометрии большое внимание уделяется углам - угол является одной из основных характеристик любой фигуры. Угол представляет собой область плоскости, ограниченную двумя полупрямыми, называемыми сторонами угла, и общим началом, называемым вершиной угла. Однако, не все углы равны по величине - некоторые углы могут быть меньше или больше других.
Один угол считается меньше другого, если его величина (мера) меньше величины другого угла. Для измерения углов используется система меры углов, представляющая собой деление полного угла на 360 равных частей, называемых градусами. Каждый градус можно дополнительно разделить на минуты и секунды, для более точного определения величины угла. Мера угла определяется с помощью специальных инструментов - угломеров или процесса измерения длин сторон угла и их сравнения с известными углами.
Меньший угол может быть определен с помощью различных методов. Например, если углы имеют одинаковую вершину, а одна сторона первого угла лежит на продолжении другой стороны второго угла, то первый угол считается меньше второго. Также, можно определять меньший угол путем сравнения их мер - если величина одного угла меньше величины другого, то первый угол считается меньше. Определение меньшего и большего угла играет важную роль в геометрии, так как позволяет сравнивать и классифицировать углы и фигуры на основе их свойств и характеристик.
Что значит, что один угол меньше другого
Когда говорят, что один угол меньше другого, имеют в виду их числовые значения, а не их физический размер. Углы могут быть измерены в градусах (°), радианах (rad) или градах (gon). Когда один угол имеет меньшее числовое значение, это означает, что он охватывает меньшую часть полной окружности или поворота.
Однако, важно помнить, что угол - это не только его числовое значение, но и его положение в пространстве. Два угла могут иметь одинаковое числовое значение, но быть расположенными по-разному. Например, два угла по 45° могут быть расположены в разных положениях относительно других линий или поверхностей, что делает их визуально разными.
Поэтому, если говорят, что один угол меньше другого, это означает, что его числовое значение меньше, и мы сравниваем их величины. Важно учитывать контекст и положение углов, чтобы правильно понимать, что означает, что один угол меньше другого.
Понятие угла и его размеры
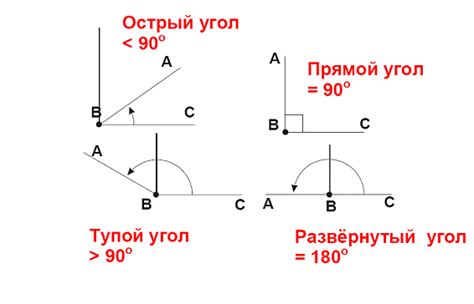
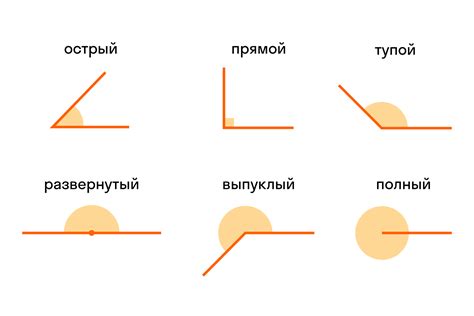
Размер угла определяется величиной его отклонения от прямого угла, который составляет 90 градусов. Если угол меньше прямого, то говорят, что он острый. Острый угол имеет размер меньше 90 градусов, но больше нуля. Если угол равен 90 градусам, его называют прямым углом. Если угол больше прямого, то он называется тупым. Тупой угол имеет размер больше 90 градусов, но меньше 180 градусов.
Таким образом, когда говорят, что один угол меньше другого, это означает, что размер первого угла меньше размера второго.
Свойства углов и их виды
Углы могут быть положительными и отрицательными. Положительный угол имеет направление против часовой стрелки, а отрицательный - по часовой стрелке. Нулевой угол является особым случаем, он представляет собой прямую линию и не имеет острой вершины.
В зависимости от величины, углы могут быть разделены на три вида:
| Меньший угол | Больший угол | Прямой угол |
|---|---|---|
| Угол, значение которого меньше 90 градусов, называется меньшим углом. Он имеет острую вершину и открытый вид. | Угол, значение которого больше 90 градусов, называется большим углом. Он имеет тупую вершину и открытый вид. | Угол, значение которого равно 90 градусов, называется прямым углом. Он имеет острый вершину и закрытый вид. |
Знание свойств углов и их видов является важным для решения геометрических задач и построения точных геометрических фигур.
Сравнение углов по размеру
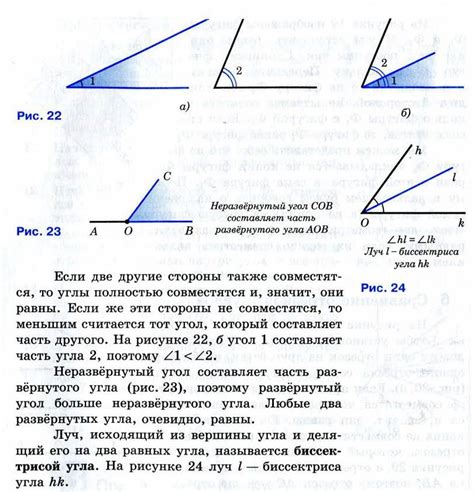
Для сравнения углов необходимо смотреть на их величину, измеренную в градусах. Угол считается меньше другого угла, если его мера оказывается меньше меры второго угла. То есть, если угол А имеет меру 40 градусов, а угол В - 60 градусов, то угол А будет меньше угла В.
Однако, необходимо помнить, что сравнение углов не всегда является простым процессом. Взгляды на углы могут быть искажены из-за перспективы или искажений объекта. Поэтому при сравнении углов важно учитывать контекст и способ определения их величины.
Сравнение углов по размеру не только помогает в геометрии, но также имеет практическое применение в повседневной жизни. Например, в архитектуре и дизайне, сравнение углов позволяет создавать баланс и гармонию в проектах. Также, сравнение углов может использоваться при решении задач физики и инженерии.
Методы измерения углов
Существует несколько методов измерения углов:
Протектором: для этого метода используется инструмент под названием протектор, который позволяет с легкостью измерять и строить углы. Протектор представляет собой сгибаемый инструмент с зубчиками и наклонными рисками, которые позволяют точно измерить углы с помощью разметки на бумаге или другой поверхности.
Гониометром: гониометр - это особый инструмент, который специально разработан для измерения углов. Он состоит из полукруглой дуги, на которой расположена шкала градусов. Гониометр позволяет измерять углы с высокой точностью, используя наклонный индикатор или специальный лазерный прибор.
Координатным методом: этот метод основан на математических принципах и использует координатную плоскость для измерения углов. Угол измеряется как отклонение от расположенных в начале координат осей X и Y. Для измерения углов с помощью координатного метода необходимо знать координаты начальной и конечной точек.
Измерение углов является важным навыком в геометрии и науке, и правильное использование метода измерения помогает достичь более точных результатов при решении математических задач и построении фигур.
Примеры задач

Рассмотрим несколько примеров задач, связанных с определением того, что один угол меньше другого:
- Найдите два угла треугольника, если известно, что один из них меньше другого.
- Определите, являются ли два угла в параллелограмме равными, если один из них меньше другого.
- Пусть имеется прямоугольный треугольник, у которого один угол равен 30 градусам. Найдите меньший угол треугольника.
- В равнобедренном треугольнике один из углов основания равен 60 градусам. Определите меньший угол треугольника.
Для решения этих задач необходимо знать основные свойства углов и их сравнение. Если один угол меньше другого, это означает, что его величина численно меньше, чем второго угла. Поэтому в каждом из примеров необходимо использовать известные свойства углов и математические операции для нахождения решения.
Значение углов в практической жизни
Понимание значения углов имеет важное практическое значение в различных областях нашей жизни. Углы широко используются в геометрии, строительстве, архитектуре, физике и других науках.
Одно из основных практических приложений углов - измерение и построение. Мы используем углы для определения размеров и форм объектов. Например, в строительстве углы помогают нам правильно установить стены или разметить фундамент. В архитектуре, углы используются для создания гармоничного дизайна и симметрии зданий.
В физике углы имеют большое значение при изучении движения, напряжения и других физических явлений. Они помогают нам понять взаимоотношения и влияние сил и напряжений на объекты.
Также углы используются в навигации и геодезии. Они облегчают измерение и определение направлений и расстояний на местности.
Понимание значения углов также полезно для повседневных задач. Например, при парковке автомобиля, знание углов поможет выбрать правильное положение и угол поворота. В кулинарии, углы используются при нарезке продуктов, чтобы получить ровные и правильные куски.
Таким образом, знание значения углов в практической жизни играет важную роль во множестве областей, помогая нам измерять, конструировать, анализировать и улучшать наши задачи и процессы.



