Дроби - это очень важная тема в математике, особенно в 6 классе. На первый взгляд они могут показаться сложными и запутанными, но на самом деле дроби - это не так уж и сложно. В этой статье мы расскажем вам все, что вы должны знать о дробях и поделимся полезными правилами.
Во-первых, что такое дробь? Дробь - это число, которое представлено двумя числами - числителем и знаменателем, разделенными горизонтальной чертой. Числитель показывает, сколько частей мы берем, а знаменатель показывает, на сколько частей делится целое. Например, если у нас есть дробь 1/2, это означает, что мы берем одну часть из двух возможных.
Дроби можно складывать, вычитать, умножать и делить, но для этого сначала нужно привести дроби к общему знаменателю. Правило приведения дробей к общему знаменателю достаточно простое - нужно найти наименьшее общее кратное (НОК) знаменателей и заменить каждую дробь на эквивалентную ей с общим знаменателем. Например, если у нас есть дроби 1/2 и 1/3, то мы должны привести их к общему знаменателю 6, и получим 3/6 и 2/6 соответственно.
Знание дробей очень полезно в жизни. Они используются для расчетов долей и процентов, в рецептах, при работе с деньгами и многих других ситуациях. Поэтому очень важно хорошо понимать и уметь работать с дробями. Надеемся, что эта статья поможет вам разобраться и узнать больше о дробях!
Что мы знаем о дробях 6 класс

Дроби используются для представления долей, частей целого числа или величины. Они играют ключевую роль в решении задач, связанных с долями, процентами, длинами, площадями и объемами.
Основные правила работы с дробями в 6 классе:
- Сложение и вычитание дробей: Необходимо привести дроби к общему знаменателю, затем складывать или вычитать числители и оставить знаменатель без изменений.
- Умножение дробей: Для умножения дробей, нужно умножить числитель первой дроби на числитель второй дроби и знаменатель первой на знаменатель второй, затем сократить полученную дробь до несократимого вида, если это возможно.
- Деление дробей: Для деления дробей, нужно умножить первую дробь на обратную второй дробь (знаменатель и числитель меняются местами), затем сократить полученную дробь до несократимого вида.
Правила работы с дробями применяются во многих задачах и ситуациях повседневной жизни, поэтому важно освоить их хорошо. Практика и решение задач помогут лучше понять и запомнить правила работы с дробями.
Определение дробей и их основные свойства
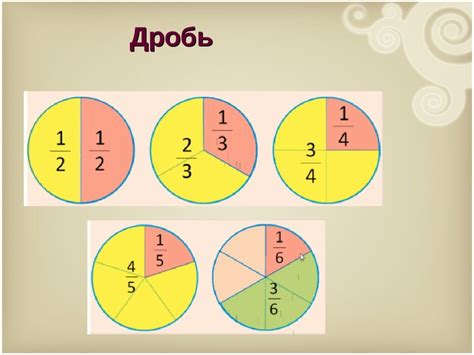
Дробь позволяет выразить отношение целого числа к целому числу. Например, дробь 2/3 означает, что у нас есть две части из трех возможных.
Основные свойства дробей:
- Если дроби имеют одинаковый знаменатель, то их числители можно складывать и вычитать.
- Если дроби имеют одинаковый знаменатель, то их числители можно умножать и делить.
- Дроби можно сравнивать - для этого необходимо сравнить их числители.
- Если числитель и знаменатель дроби умножить или разделить на одно и то же число, то значение дроби не изменится.
- Если дробь умножить или разделить на 1, то она останется равной исходной дроби.
Знание основных свойств дробей позволяет успешно работать с ними и решать задачи по их упрощению, сложению, вычитанию, умножению и делению.
Правила сложения и вычитания дробей
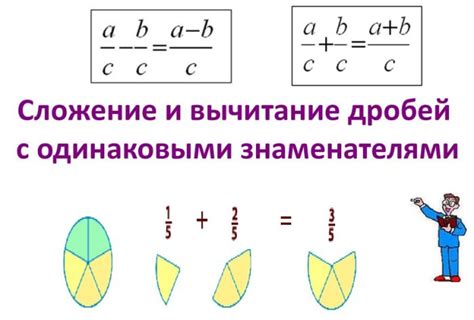
Для того чтобы сложить или вычесть дроби, необходимо выполнить несколько шагов
- Найти общий знаменатель у дробей, которые нужно сложить или вычесть. Используй наименьшее общее кратное знаменателей дробей.
- Привести все дроби к общему знаменателю путем умножения числителей и знаменателей на соответствующие множители.
- Если знаменатели дробей равны, то приводить дроби не нужно.
- Сложить или вычесть числители дробей (или те, и другие).
- Записать полученную дробь с найденным ранее общим знаменателем.
- Если полученная дробь оказалась несократимой, сократить ее до минимального вида.
Ниже представлен пример сложения двух дробей:
Дано: $frac{3}{4} + frac{1}{6}$
- Находим общий знаменатель: $lcm(4, 6) = 12$
- Приводим дроби к общему знаменателю:
- $frac{3}{4} = frac{3}{4} * frac{3}{3} = frac{9}{12}$
- $frac{1}{6} = frac{1}{6} * frac{2}{2} = frac{2}{12}$
- Складываем числители: $9 + 2 = 11$
- Записываем результат с общим знаменателем: $frac{11}{12}$
- Сокращаем дробь до минимального вида: $frac{11}{12}$
Итак, сумма дробей $frac{3}{4} + frac{1}{6}$ равна $frac{11}{12}$.
Примеры задач на сложение и вычитание дробей

1. Задача на сложение:
Вова купил 2/3 килограмма яблок и 1/4 килограмма груш. Сколько всего килограммов фруктов он купил?
Решение:
Для сложения дробей необходимо, чтобы знаменатели были одинаковыми. Приведем дроби к общему знаменателю, который в данном случае будет равен 12:
2/3 = 8/12
1/4 = 3/12
Теперь можно сложить числители:
8/12 + 3/12 = 11/12
Ответ: Вова купил 11/12 килограмма фруктов.
2. Задача на вычитание:
У Маши было 3/5 пирожка, и она съела 1/5 пирожка. Сколько пирожков осталось у Маши?
Решение:
Для вычитания дробей знаменатель должен быть одинаковым. Приведем дроби к общему знаменателю, который в данном случае будет равен 5:
3/5 - 1/5 = 2/5
Ответ: У Маши осталось 2/5 пирожка.
Правила умножения и деления дробей

Правило умножения дробей:
Для умножения дробей необходимо перемножить числители и знаменатели. То есть, если у нас есть дроби a/b и c/d, то их произведение будет равно (a*c)/(b*d). Например, чтобы умножить 1/3 на 2/5, мы должны умножить числитель 1 на 2 и знаменатель 3 на 5, что даст нам результат 2/15.
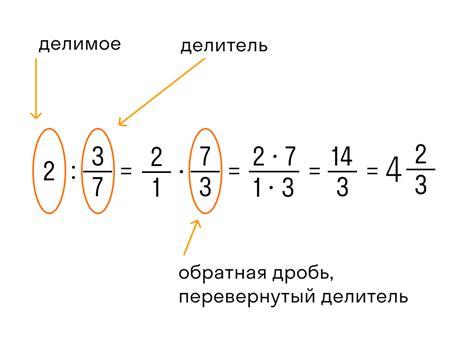
Правило деления дробей:
Для деления дробей необходимо помножить первую дробь на обратную второй дроби. Обратная дробь получается, если поменять числитель и знаменатель местами. То есть, если у нас есть дроби a/b и c/d, то результат деления будет равен (a/b)*(d/c)= (a*d)/(b*c). Например, чтобы разделить 2/3 на 4/5, мы должны умножить 2/3 на 5/4, что даст нам результат 10/12 или 5/6.
Запомни эти правила умножения и деления дробей, и ты сможешь легко выполнять эти операции. Практикуйся на примерах, чтобы лучше понять их применение.
Примеры задач на умножение и деление дробей
- Задача 1: Умножить дробь 3/5 на дробь 2/3.
- Задача 2: Разделить дробь 1/4 на дробь 2/3.
- Задача 3: Упростить дробь 10/15.
Решение: Чтобы умножить дроби, нужно умножить их числители между собой и знаменатели между собой. В данном случае получим 3 * 2 / 5 * 3 = 6/15. Итак, результатом умножения будет дробь 6/15.
Решение: Чтобы разделить дроби, нужно умножить делимую дробь на обратную дробь, то есть числитель станет знаменателем, а знаменатель - числителем. В данном случае получим 1/4 * 3/2 = 3/8. Итак, результатом деления будет дробь 3/8.
Решение: Чтобы упростить дробь, нужно найти их наибольший общий делитель (НОД) числителя и знаменателя и поделить оба числа на этот НОД. В данном случае НОД чисел 10 и 15 равен 5. Поделив числитель и знаменатель на 5, получим упрощенную дробь 2/3.
Зная основные правила и используя примеры задач, вы сможете успешно решать задачи на умножение и деление дробей. Постепенно у вас будут сложнее задачи, но практика поможет вам стать опытным в решении таких задач.
Приведение дробей к общему знаменателю
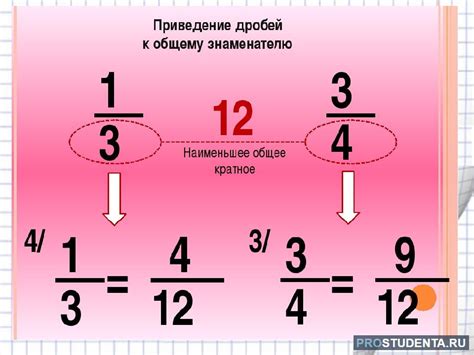
Если у нас есть две дроби с разными знаменателями, то чтобы привести их к общему знаменателю, нужно найти их наименьшее общее кратное (НОК) знаменателей. НОК - это наименьшее число, которое делится на оба знаменателя без остатка.
Процесс приведения дробей к общему знаменателю можно представить следующим образом:
| Исходные дроби | Приведение к общему знаменателю |
|---|---|
| $$\frac{a}{b}$$ | $$\frac{a \cdot k}{b \cdot k}$$ |
| $$\frac{c}{d}$$ | $$\frac{c \cdot k}{d \cdot k}$$ |
Где $$k$$ - это некоторое число, которое мы выбираем, чтобы знаменатели стали равными.
После приведения дробей к общему знаменателю, мы можем выполнять операции над ними. Например, для сложения дробей нам необходимо сложить числители дробей и оставить знаменатель неизменным.
Важно помнить, что после выполнения арифметических операций с дробями, результат нужно упростить, если это возможно. Для упрощения дроби необходимо найти их наибольший общий делитель (НОД) и поделить числитель и знаменатель на этот НОД.
Сокращение дробей до несократимого вида

Для сокращения дроби, необходимо найти их наибольший общий делитель (НОД) числителя и знаменателя. НОД – это наибольшее число, на которое можно одновременно поделить и числитель, и знаменатель.
Сокращение дробей до несократимого вида может быть выполнено следующим образом:
- Разложите числитель и знаменатель на простые множители.
- Найдите общие простые множители числителя и знаменателя.
- Укажите эти общие простые множители и возведите их в наименьшие степени.
- Если после сокращения дроби еще остались общие множители числителя и знаменателя, продолжите сокращение.
- Полученная дробь будет в несократимом виде.
Пример:
Рассмотрим дробь 12/18 и будем сокращать ее.
1. Разложим числитель (12) и знаменатель (18) на простые множители: 12 = 2 * 2 * 3 и 18 = 2 * 3 * 3.
2. Найдем общие простые множители: 2 и 3.
3. Возведем общие простые множители в наименьшие степени: 2 * 3 = 6.
4. Проверим, остались ли еще общие множители: нет, значит дробь 12/18 не может быть сокращена дальше.
5. Полученная дробь 12/18 является несократимой.
Сокращение дробей до несократимого вида очень важно при выполнении различных операций с дробями, таких как сложение, вычитание, умножение и деление. Несократимый вид дроби позволяет упростить расчеты и получить точный результат.
Знание правил сокращения дробей до несократимого вида поможет вам успешно решать задачи и использовать дроби в повседневной жизни.
Примеры задач на приведение и сокращение дробей

Пример 1: Проведя вычисления, приведите дробь к несократимой форме: 24/36.
Решение: Для приведения дроби к несократимой форме, нужно найти их наибольший общий делитель (НОД) и поделить числитель и знаменатель на этот НОД. В данном случае, НОД для чисел 24 и 36 равен 12. Поделив числитель и знаменатель на 12, получим дробь в несократимой форме: 2/3.
Пример 2: Найдите несократимую форму для дроби 12/18.
Решение: Чтобы найти несократимую форму дроби, нужно найти их наибольший общий делитель и поделить числитель и знаменатель на него. В данном случае, НОД для чисел 12 и 18 равен 6. Поделив числитель и знаменатель на 6, получим дробь в несократимой форме: 2/3.
Пример 3: Приведите дробь 16/24 к несократимой форме.
Решение: Чтобы привести дробь к несократимой форме, нужно найти их наибольший общий делитель и поделить числитель и знаменатель на него. В данном случае, НОД для чисел 16 и 24 равен 8. Поделив числитель и знаменатель на 8, получим дробь в несократимой форме: 2/3.
Надеемся, что эти примеры задач помогут вам улучшить ваше понимание приведения и сокращения дробей. Продолжайте практиковаться, и скоро вы сможете решать задачи этой темы легко и быстро.



