Параллелограмм – это четырехугольник, у которого противоположные стороны равны по длине и параллельны друг другу. Один из самых известных примеров параллелограмма – прямоугольник. Диагонали параллелограмма – это отрезки, соединяющие его противоположные вершины. Интересно, что диагонали параллелограмма пересекаются в одной точке и делятся пополам.
Для доказательства этого факта можно использовать свойства параллелограмма. Рассмотрим одну из диагоналей параллелограмма и проведем медиану к ней. Медиана – это отрезок, соединяющий вершину с серединой противоположной стороны. Поскольку противоположные стороны параллельны, медиана будет делить диагональ пополам. Таким образом, точка пересечения диагоналей параллелограмма будет являться серединой каждой из них.
Другой способ доказательства заключается в использовании геометрической симметрии. Параллелограмм обладает осью симметрии, которая проходит через точку пересечения диагоналей. По определению, точка пересечения является центром симметрии фигуры. Симметричность параллелограмма гарантирует, что диагонали будут делиться пополам.
Что такое параллелограмм
В параллелограмме все углы также равны и смежные углы дополнительны. Также важно отметить, что диагонали параллелограмма делятся пополам точкой пересечения. Это значит, что точка пересечения диагоналей находится на равном удалении от вершин параллелограмма.
Диагонали параллелограмма также имеют ряд особенностей. Они равны по длине и делятся пополам точкой пересечения. Кроме того, каждая диагональ является осью симметрии параллелограмма, что означает, что если мы отразим параллелограмм относительно одной из его диагоналей, то получим фигуру, совмещающуюся с исходным параллелограммом.
Параллелограммы широко используются в геометрии и имеют много практических применений. Их свойства, такие как параллельность сторон и углов, делают их полезными для конструкций и вычислений. Более того, многие другие геометрические фигуры, такие как прямоугольник, ромб и квадрат, являются разновидностями параллелограмма.
Определение и свойства параллелограмма
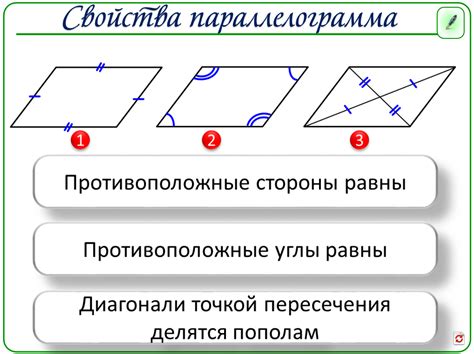
У параллелограмма есть несколько важных свойств:
- Противоположные стороны параллелограмма равны по длине.
- Противоположные углы параллелограмма равны по величине.
- Диагонали параллелограмма делятся пополам в точке их пересечения.
- Сумма углов параллелограмма равна 360 градусов.
Также, у параллелограмма есть несколько следствий из этих свойств:
- Диагонали параллелограмма равны по длине.
- Противоположные углы параллелограмма дополняют друг друга до 180 градусов.
- Напротив каждого угла параллелограмма находится его собственная пара равных и смежных углов.
| Свойство | Иллюстрация |
|---|---|
| Противоположные стороны равны | А------------B | | | | D------------C |
| Противоположные углы равны | A ---- B | | | | D ---- C |
| Диагонали делятся пополам | A / \ / \ / \ / \ /_ _ _ _ _\ B C \_ _ _ _ _/ D |
| Сумма углов равна 360° | A ---- B | | | | D ---- C |
Диагонали параллелограмма
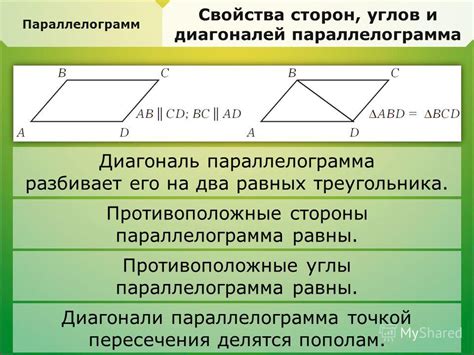
Главное свойство диагоналей параллелограмма заключается в том, что они делятся точкой пересечения пополам. Это означает, что расстояние от точки пересечения до каждого из концов диагоналей равно. Другими словами, диагонали параллелограмма делят его на четыре равные треугольных площади.
Из данного свойства следует, что длина каждой диагонали параллелограмма равна сумме длин двух векторов, образованных его сторонами. Векторы, образованные сторонами параллелограмма, равны по длине и противоположно направлены. Поэтому сумма длин векторов будет равна нулю, что означает, что длина каждой диагонали также равна нулю.
Другое важное свойство диагоналей параллелограмма заключается в том, что они пересекаются под прямым углом. Это означает, что диагонали параллелограмма являются взаимно перпендикулярными.
Таким образом, диагонали параллелограмма играют важную роль при изучении его свойств и вычислении площади и периметра параллелограмма. Они делят фигуру на равные части и образуют прямой угол, что делает их полезными элементами для решения геометрических задач.
Определение и свойства диагоналей
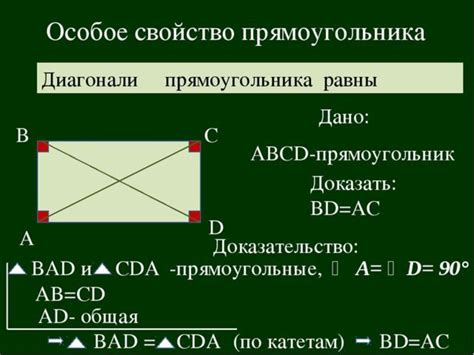
Основное свойство диагоналей параллелограмма заключается в том, что они делятся точкой пересечения пополам. Это означает, что длина каждой диагонали равна полусумме длин двух других диагоналей.
Кроме того, диагонали параллелограмма являются биссектрисами углов, образованных этими диагоналями и сторонами параллелограмма. Это означает, что каждая диагональ делит соответствующий угол на два равных угла.
Также, диагонали параллелограмма являются взаимно перпендикулярными. Это означает, что они пересекаются под прямым углом.
Диагонали параллелограмма также обладают свойством равенства, то есть две диагонали равны друг другу. Это свойство следует из факта, что параллелограмм является частным случаем ромба.
Знание свойств диагоналей параллелограмма позволяет более глубоко понять строение и связи между элементами этой геометрической фигуры, а также использовать их в решении задач и построениях.
Точка пересечения диагоналей параллелограмма

Точка пересечения диагоналей параллелограмма делит каждую из них пополам. Это значит, что расстояние от вершины параллелограмма до точки пересечения диагоналей равно половине длины диагонали. Можно сказать, что эта точка является центром симметрии параллелограмма. В математической терминологии точка пересечения диагоналей называется центром параллелограмма.
Свойства точки пересечения диагоналей в параллелограмме:
- Расстояние: Расстояние от вершины параллелограмма до точки пересечения диагоналей равно половине длины диагонали.
- Центр симметрии: Точка пересечения диагоналей является центром симметрии параллелограмма. Это значит, что относительно этой точки можно отразить фигуру так, чтобы каждая ее часть совпала с соответствующей ей противоположной частью.
- Дополнительные свойства: Точка пересечения диагоналей делит параллелограмм на четыре равных треугольника, которые имеют общую вершину - центральную вершину.
Важно отметить, что эти свойства точки пересечения диагоналей справедливы только для параллелограммов. В других четырехугольниках такие свойства может не быть.
Определение и свойства точки пересечения
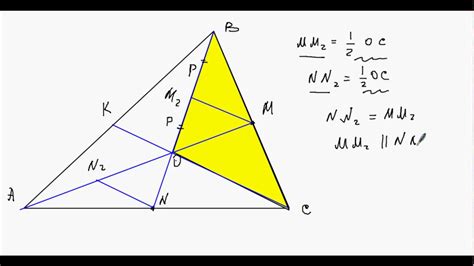
одна диагональ соединяет противоположные углы параллелограмма, а вторая - противоположные стороны.
Основные свойства точки пересечения:
- Расположение: Точка пересечения находится внутри параллелограмма, но может лежать на границе его сторон.
- Симметричность: Точка пересечения делит каждую из диагоналей пополам. Это означает, что расстояние от точки пересечения до любой из концов диагонали равно расстоянию от точки пересечения до противоположного конца диагонали.
- Уникальность: Всегда существует только одна точка пересечения внутри параллелограмма.
Знание о точке пересечения важно при решении геометрических задач, связанных с параллелограммами. Она помогает определить симметричные отношения и делает анализ фигуры более легким и понятным.
Деление диагоналей пополам
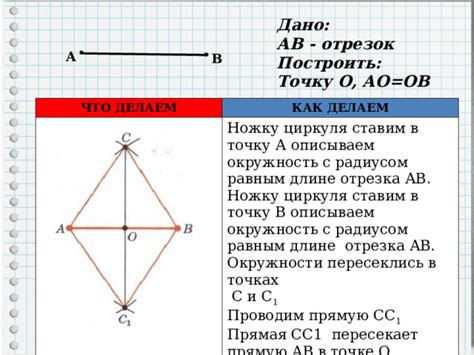
Пусть ABCD - параллелограмм, а AC и BD - его диагонали. Пусть точка пересечения диагоналей обозначается как O. Тогда можно утверждать, что точка O делит диагонали AC и BD пополам.
Это свойство можно доказать с помощью геометрических рассуждений:
Доказательство:
Рассмотрим треугольник AOC. В этом треугольнике у нас есть две пары равных сторон: AO=CO и AC=AC. По свойству равных сторон углы, противолежащие им, равны. Из этого следует, что угол AOC равен углу COA.
Таким же образом можно рассмотреть треугольник BOD и заметить, что угол BOD равен углу DOB.
Поскольку угол AOC равен углу COA, а угол BOD равен углу DOB, то мы можем заключить, что треугольники AOC и BOD являются подобными. Они имеют два равных угла и соответственные стороны пропорциональны.
Из подобия треугольников AOC и BOD следует, что отношение длины AO к длине AC равно отношению длины BO к длине BD.
Таким образом, если мы обозначим отрезки AO и BO как x, а отрезки AC и BD как d, то мы можем записать следующее:
x / d = x / d
Отсюда следует, что у нас есть равенство:
x = x
Таким образом, мы доказали, что точка O делит диагонали параллелограмма пополам, что и требовалось доказать.
Как диагонали делятся пополам в параллелограмме?
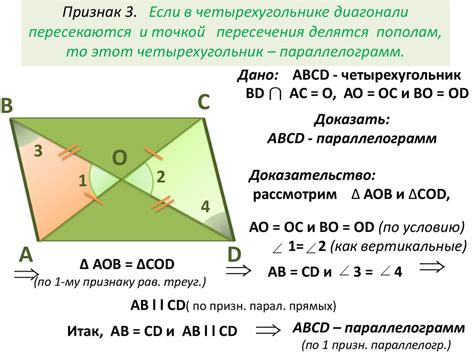
Диагонали параллелограмма - это отрезки, соединяющие противоположные вершины. Одним из очень интересных свойств параллелограмма является то, что его диагонали делятся пополам. Это означает, что точка их пересечения (точка пересечения диагоналей) делит каждую диагональ пополам.
Математически это можно выразить следующим образом: если AC и BD - диагонали параллелограмма ABCD, то точка пересечения диагоналей O делит каждую диагональ пополам, то есть:
| OA = OC | OB = OD |
Это свойство можно доказать с помощью геометрических соображений или с использованием векторных методов. Но самый простой способ доказательства заключается в использовании свойств параллелограмма.
Заметим, что в параллелограмме противоположные стороны равны, а значит их векторы равны. Таким образом, векторы AB и CD равны между собой, а векторы BC и AD также равны. Поскольку точка O - середина отрезка AB (так как диагонали делятся пополам), вектор AO равен вектору OB. Аналогично, вектор CO равен вектору OD.
Таким образом, мы доказали, что в параллелограмме точка пересечения диагоналей делит каждую диагональ пополам.
Соотношение длин диагоналей
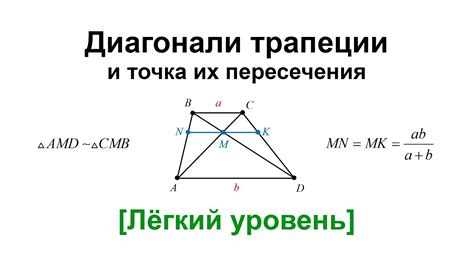
В параллелограмме диагонали делятся точкой пересечения пополам. Это значит, что каждая диагональ располагается между двумя равными отрезками, а соотношение длин диагоналей будет равно единице.
Пусть одна диагональ параллелограмма равна AB, а другая диагональ - CD. Тогда можно записать следующие равенства:
AB = 2x, где x - равенство отрезков AM и MB, где M - точка пересечения диагоналей.
CD = 2y, где y - равенство отрезков CM и DM, где M - точка пересечения диагоналей.
Так как диагонали делятся пополам, то справедливо следующее равенство:
AB = CD
2x = 2y
Упрощая равенство, получим:
x = y
Таким образом, соотношение длин диагоналей в параллелограмме всегда равно 1:1.
Формула соотношения длин диагоналей

| Длина первой диагонали | : | Длина второй диагонали | = | Сумма длин двух сторон | : | Разница длин двух сторон |
Таким образом, формула для соотношения длин диагоналей параллелограмма записывается следующим образом:
Диагональ 1 : Диагональ 2 = (Сторона 1 + Сторона 2) : (Сторона 1 - Сторона 2)
Где сторона 1 и сторона 2 - стороны параллелограмма, а Диагональ 1 и Диагональ 2 - соответственно первая и вторая диагонали.
Используя данную формулу, можно легко найти соотношение длин диагоналей любого параллелограмма, зная длины его сторон.
Практическое применение

Понимание принципа деления диагоналей параллелограмма пополам может быть полезным при решении различных задач и проблем.
В архитектуре и строительстве знание этого принципа позволяет более точно планировать и проектировать здания и сооружения. Например, при создании плана помещения можно использовать этот принцип для определения оптимального места для расположения точки доступа к интернету или для размещения различных электрических розеток.
В графическом дизайне принцип деления диагоналей пополам может использоваться для создания более гармоничного и сбалансированного композиционного решения. Например, равное деление диагоналей может быть использовано для размещения текстовых и графических элементов на дизайне веб-сайта или рекламного баннера.
В математике этот принцип может быть использован для доказательства различных теорем и задач. Например, для доказательства равенства площадей треугольников можно использовать принцип равного деления диагоналей параллелограмма.
Наконец, в повседневной жизни понимание этого принципа может помочь нам принять рациональные решения. Например, при выборе между двумя вариантами, можно оценить их преимущества и недостатки, используя принцип деления диагоналей пополам.
Таким образом, практическое применение принципа деления диагоналей параллелограмма пополам находится в различных областях нашей жизни, где он может помочь нам принять правильные решения и достичь гармонии и баланса.
Примеры использования деления диагоналей пополам в задачах
Найти площадь параллелограмма:
Площадь параллелограмма можно найти, зная длины его сторон и одну из его высот. Если диагонали параллелограмма делятся пополам, то они равны между собой и являются его высотами. Тогда площадь параллелограмма можно вычислить как произведение длины одной из его диагоналей на любую сторону.
Доказать, что четырехугольник – параллелограмм:
Найти координаты точки пересечения диагоналей:
Если известны координаты вершин параллелограмма, то можно найти координаты точки пересечения его диагоналей. Если диагонали делятся пополам, то координаты этой точки можно найти как полусумму координат вершин.
Таким образом, деление диагоналей пополам является важным свойством параллелограмма и находит широкое применение при решении различных задач и доказательств в математике.



