Треугольник - одна из основных и наиболее изучаемых геометрических фигур. Он обладает множеством особенностей и интересных свойств. Одно из таких свойств - деление противоположной стороны пополам. Но почему это свойство так важно и как оно работает?
Деление противоположной стороны пополам основано на теореме, известной как Теорема о биссектрисе треугольника. Согласно этой теореме, биссектриса угла треугольника делит противоположную ему сторону на две части, пропорциональные двум другим сторонам треугольника. Иными словами, отношение длины одной части к длине другой части равно отношению длины смежной стороны к длине противоположной стороны.
Такое деление находит много применений в геометрии и физике. Например, оно может использоваться для нахождения высоты треугольника или расчета углов треугольника. Оно также является важным элементом при проектировании и конструировании различных объектов и сооружений. Знание и понимание этого свойства треугольников позволяет математикам и инженерам эффективно решать задачи и создавать новые технологические решения.
Биссектриса противоположного угла
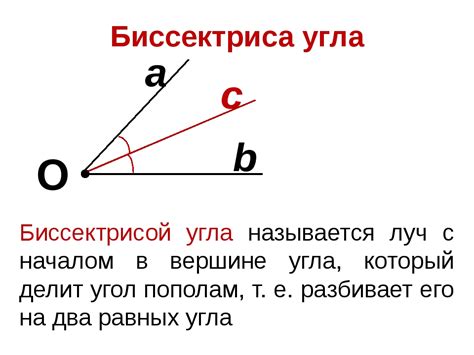
Биссектрисой противоположного угла называется отрезок, который делит противоположный угол треугольника на две равные части и прямоугольный проводит к противоположной стороне.
Биссектриса противоположного угла является одной из важных линий в треугольнике. Она имеет ряд свойств и применений.
- Биссектриса противоположного угла является внутренним угловым биссектрисом треугольника.
- Биссектриса противоположного угла делит противоположную сторону треугольника на отрезки, пропорциональные длинам смежных сторон.
Применение биссектрис противоположных углов заключается в решении различных задач по построению и вычислению треугольников. Зная длину биссектрисы и длины двух смежных сторон, можно найти длину противоположной стороны.
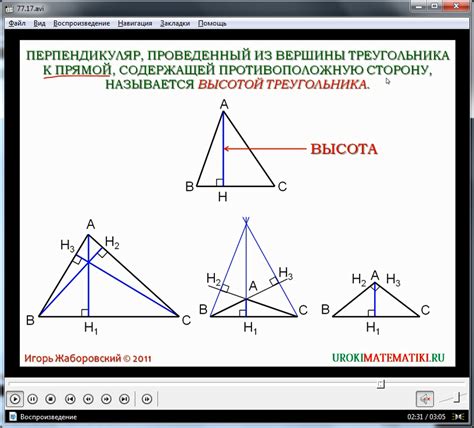
Перпендикуляр, проведенный из вершины
Для построения перпендикуляра, проведённого из вершины треугольника, необходимо следующее:
- Выбрать вершину треугольника, из которой будет проводиться перпендикуляр.
- Прокладывать прямую линию, проходящую через выбранную вершину и перпендикулярную соответствующей боковой стороне.
Этот перпендикуляр разделяет треугольник на две равные части и называется высотой треугольника. Он также является основой для вычисления различных параметров треугольника, таких как площадь или углы.
Построение перпендикуляра, проведённого из вершины треугольника, является важным инструментом в геометрии и широко применяется при решении различных задач и заданий, связанных с треугольниками.
Медиана, идущая из вершины
Медианы делят сторону треугольника на две равные части. Точка, в которой медиана пересекает сторону, называется серединой этой стороны и является серединой отрезка, на который сторона делится медианой.
Медиана, идущая из вершины, имеет несколько свойств:
- Медиана, идущая из вершины, равна половине длины стороны, с которой она образует угол.
- Медиана, идущая из вершины, делит противоположную сторону пополам.
- Центр тяжести, через который проходят все медианы, делит медианы пополам.
Медианы являются важным элементом треугольника и находят применение в решении различных задач геометрии и механики.
Высота, опущенная из вершины
Высота имеет особое значение, так как она является основой для вычисления площади треугольника. Длина высоты может быть найдена с использованием теоремы Пифагора или теоремы о высоте треугольника.
Теорема Пифагора: Если треугольник прямоугольный, то квадрат длины высоты равен произведению длин отрезков, на которые высота делит гипотенузу - наибольшую сторону прямоугольного треугольника.
Теорема о высоте треугольника: Длина высоты треугольника, опущенной из вершины на сторону противоположную этой вершине, равна произведению длин двух отрезков прямой, на которую эта высота делит.
Высота, опущенная из вершины, может быть использована для решения различных геометрических и геодезических задач, а также имеет важное значение в теории треугольников.
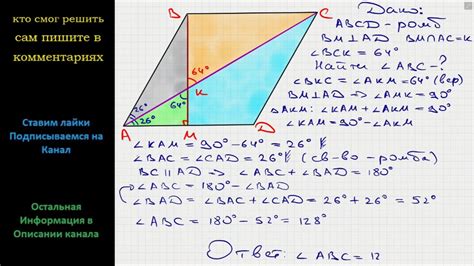
Биссектриса, исходящая из вершины
В треугольнике существует специальная линия, называемая биссектрисой, которая делит противоположную сторону пополам. Биссектриса исходит из вершины треугольника и делит угол на две равные половины. Таким образом, она делит противоположную сторону треугольника пополам и создает две равные отрезки.
Биссектриса имеет важное значение в геометрии, так как она служит одним из инструментов для решения различных задач. Например, с ее помощью можно найти точку пересечения биссектрис трех углов треугольника, называемую центром вписанной окружности. Также биссектриса может помочь в построении треугольника, если известны значения сторон и одного угла.
 | Для нахождения биссектрисы, исходящей из вершины, можно использовать следующую формулу: Bi = (√(a * b * (a + b + c) * (a + b - c))) / (a + b) Где:
|
Таким образом, биссектриса, исходящая из вершины, является важным элементом в геометрии треугольника, который позволяет находить решения для различных задач и строить треугольники на основе известных параметров.
Серединный перпендикуляр противоположной стороны
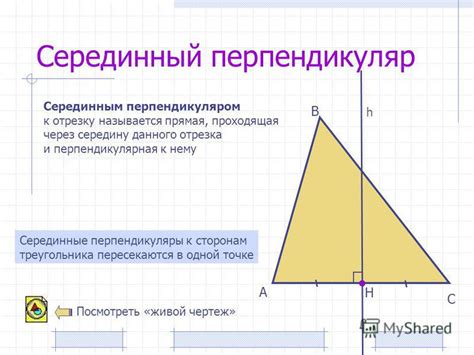
Серединный перпендикуляр противоположной стороны является осевой симметрией треугольника, то есть делит его пополам. Это значит, что если провести серединный перпендикуляр к противоположной стороне, то он разделит треугольник на два равных по площади треугольника.
Из этого следует, что длина серединного перпендикуляра равна половине длины противоположной стороны. Также стоит отметить, что серединный перпендикуляр является биссектрисой угла, образованного противоположной стороной и остальными двумя сторонами треугольника.



