Логарифмы - это математическая операция, которая позволяет нам решать различные задачи, связанные с экспоненциальными функциями. Логарифмы с разными основаниями имеют свои особенности и требуют специального подхода при их вычислении. В данной статье мы рассмотрим подробную инструкцию по счету логарифмов с различными основаниями и узнаем, как правильно использовать основные формулы и правила.
Первым шагом необходимо понять, как выглядят основные формулы для вычисления логарифмов с разными основаниями. Для логарифма с основанием a, где a - положительное число и a ≠ 1, формула будет выглядеть следующим образом:
loga(x) = y, где x - основание логарифма, a - основание, y - значение логарифма
Основные правила для вычисления логарифмов с разными основаниями включают:
- Смена основания: loga(x) = logb(x) ÷ logb(a), где a и b - разные основания
- Произведение: loga(xy) = loga(x) + loga(y)
- Деление: loga(x / y) = loga(x) - loga(y)
- Возведение в степень: loga(xn) = n * loga(x), где n - натуральное число
Следуя этой подробной инструкции и правилам, вы сможете легко и точно считать логарифмы с различными основаниями. Помните, что практика и упорство в изучении этой математической операции помогут вам стать опытным и уверенным в решении сложных задач.
Основные понятия логарифмов

Основание логарифма определяет, с помощью какой степени числа необходимо возвести, чтобы получить данное число. Иногда основание логарифма опускается, в этом случае считается, что основание равно 10.
Логарифмы позволяют упростить сложные математические выражения и решать уравнения, связанные с возведением чисел в степень. Они часто используются в научных и инженерных расчетах.
Логарифмы имеют ряд основных свойств, среди которых:
| Свойство | Формула |
| Логарифм произведения | logb(a·c) = logba + logbc |
| Логарифм частного | logb(a/c) = logba - logbc |
| Логарифм степени | logb(an) = n·logba |
| Смена основания логарифма | logba = logca / logcb |
Знание этих основных понятий и свойств логарифмов позволит вам с легкостью решать задачи и упрощать сложные выражения с логарифмами на практике.
Как считать натуральный логарифм

Для расчета натурального логарифма существует специальная функция во многих программных языках и калькуляторах. Она обозначается как ln(x), где x - число, для которого вы хотите найти логарифм.
Чтобы использовать функцию натурального логарифма в своих вычислениях, вам нужно ввести значение x в переменную и вызвать функцию ln(). Результат будет являться натуральным логарифмом заданного числа.
Например, если вы хотите найти натуральный логарифм числа 5, то вам нужно вызвать функцию ln(5). Результат будет примерно равен 1.60943.
Также стоит отметить, что натуральный логарифм обладает определенными свойствами. Например, ln(1) всегда равен 0, а ln(e) всегда равен 1.
Логарифмы являются мощным математическим инструментом, который может быть полезным в различных областях. Разучивание и практика расчета натурального логарифма поможет вам лучше понять его значения и применение.
Таблица натуральных логарифмов
| x | ln(x) |
|---|---|
| 1 | 0 |
| e | 1 |
| 2 | 0.69315 |
| 3 | 1.09861 |
| 4 | 1.38629 |
| 5 | 1.60943 |
| 10 | 2.30259 |
В таблице приведены значения натуральных логарифмов для некоторых известных чисел. Она может быть полезна для быстрого поиска значений и ориентирования в величинах логарифмов.
Способы вычисления десятичного логарифма
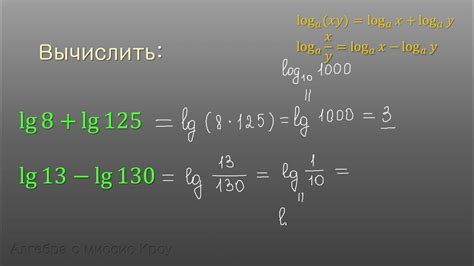
Существует несколько способов вычисления десятичного логарифма:
- Использование таблицы значений - один из самых старых и простых способов вычисления логарифма. Для этого нужно найти таблицу логарифмов, которая содержит значения логарифмов для разных чисел. Затем, найдя нужное число в таблице, можно прочитать его логарифм.
- Использование калькулятора - в большинстве научных и инженерных калькуляторов есть функция для вычисления логарифма. Для вычисления десятичного логарифма нужно нажать соответствующую кнопку (обычно обозначенную как "log", "log10" или "log10") и ввести число, для которого нужно вычислить логарифм.
- Использование математических формул - для более точного и подробного вычисления логарифма можно использовать математические формулы. Для десятичного логарифма можно использовать формулу: log10(x) = log(x) / log(10), где log(x) - натуральный логарифм числа x.
Выбор способа вычисления логарифма зависит от доступных инструментов и уровня точности, необходимого для конкретного решения задачи.
Как использовать требования точности при вычислении логарифмов

При вычислении логарифмов с разными основаниями, точность играет важную роль. Чем выше требования точности, тем более точное значение логарифма можно получить. Важно иметь в виду, что точность вычислений влияет на время выполнения и объем памяти, затрачиваемый на вычисления.
Если точность не является критическим фактором, можно использовать встроенные функции логарифма в языке программирования. Они обычно предоставляют разные основания для вычисления логарифмов. Например, в большинстве языков программирования можно использовать функцию log() для вычисления натурального логарифма (с основанием e) или функцию log10() для вычисления логарифма по основанию 10.
Однако, если требуется более высокая точность, можно использовать специальные библиотеки или алгоритмы вычисления логарифма с большей точностью. Такие библиотеки как MPFR (Multiple Precision Floating-Point Reliable) или MATLAB Symbolic Math Toolbox предоставляют возможность работать с числами высокой точности и вычислять логарифмы с заданной точностью.
При использовании библиотек, следует обратить внимание на диапазон значений, для которых гарантируется точность. Часто, для обеспечения более высокой точности, требуется использовать больше памяти или производить вычисления более длительное время.
Также, стоит помнить, что некоторые основания логарифмов могут быть сложными для вычисления с высокой точностью. Например, вычисление логарифма с основанием 2 может быть сложнее, чем логарифма с основанием 10 или е.
В итоге, выбор метода вычисления логарифма с разными основаниями зависит от требуемой точности, доступных ресурсов и особенностей конкретной задачи. При выборе метода следует обратить внимание на особенности реализации, чтобы получить наиболее точные и эффективные результаты.
Методы вычисления произвольного логарифма

Вычисление логарифма с произвольным основанием может быть не таким простым, как расчет классического натурального логарифма или десятичного логарифма. Однако существуют несколько методов, которые могут помочь в этом процессе.
- Метод замены основания. Данный метод заключается в преобразовании логарифма с произвольным основанием в логарифм с базисом, который более удобен для вычисления. Например, логарифм с основанием a может быть выражен через натуральный или десятичный логарифм следующим образом:
- loga(x) = ln(x) / ln(a), если используется натуральный логарифм (ln)
- loga(x) = log10(x) / log10(a), если используется десятичный логарифм (log10)
Выбор метода зависит от ваших предпочтений и того, какой доступный инструмент у вас есть. Независимо от выбранного метода, помните, что правильное вычисление произвольного логарифма может быть полезным при решении различных математических задач и применении в реальной жизни.
Обратные операции: как найти аргументы логарифма

Для нахождения аргументов логарифма необходимо использовать обратные операции. Если известен логарифм и его основание, то можно найти аргумент. Существуют два основных способа нахождения аргументов логарифма: используя прямую функцию возведения в степень и используя свойства логарифмов.
1. Используя прямую функцию возведения в степень:
Допустим, нам дан логарифм logb(x) = y. Чтобы найти аргумент x, необходимо применить прямую функцию возведения в степень к обоим сторонам уравнения: by = x.
Пример:
Для уравнения log2(x) = 4, применяем прямую функцию возведения в степень by = x: 24 = x. Получаем результат x = 16.
2. Используя свойства логарифмов:
Для нахождения аргумента логарифма, используя свойства логарифмов, необходимо применить обратные операции.
Пример:
Допустим, нам дано уравнение log3(2x) = 4. Применяем свойства логарифмов: 2x = 34. Затем решаем полученное уравнение: 2x = 81. Для нахождения значения x делим обе части уравнения на 2 и получаем x = 40,5.
Таким образом, зная логарифм и его основание, можно использовать прямую функцию возведения в степень или свойства логарифмов для нахождения аргумента логарифма.
Применение логарифмов в математике и физике

В математике логарифмы позволяют сократить сложные выражения и упростить проведение различных операций, таких как перемножение и деление больших чисел. Также, они помогают решать уравнения, включающие переменные с разными основаниями, и находить значения неизвестных в комплексных системах уравнений.
В физике логарифмы применяются для моделирования физических явлений и представления данных в более удобном виде. Например, логарифмический масштаб используется для представления графиков, основанных на экспоненциальном росте или убывании, таких как радиоактивный распад или затухание сигнала.
Кроме того, логарифмы играют важную роль в статистике, экономике и других областях, где требуется анализ данных и проведение численных расчетов. Понимание логарифмов и умение их применять является неотъемлемой частью математического и научного образования.
| Применение логарифмов в математике | Применение логарифмов в физике |
|---|---|
| Упрощение сложных выражений | Моделирование физических явлений |
| Решение уравнений с разными основаниями | Представление данных в более удобном виде |
| Нахождение неизвестных в комплексных системах уравнений | Использование логарифмического масштаба для графиков |
Вычисление логарифмов с помощью калькулятора

Для вычисления логарифмов с разными основаниями можно воспользоваться обычным калькулятором, следуя простым инструкциям:
| Основание | Действие | Пример |
|---|---|---|
| Основание 10 | Использовать кнопку "log" или "log10" | log(100) = 2 |
| Основание 2 | Использовать кнопку "log2" или конвертировать в основание 10 | log2(8) = log(8) / log(2) = 3 |
| Другие основания | Использовать формулу изменения основания | logb(x) = log(x) / log(b) |
Некоторые калькуляторы также предоставляют возможность вводить основание непосредственно, что значительно упрощает процесс.
Примеры решения задач с логарифмами

Для лучшего понимания применения логарифмов, рассмотрим несколько примеров решения задач:
Пример 1: Найдите значение логарифма по основанию 2 от числа 8.
Решение:
Так как 2 возводится в какую степень, чтобы получить 8, значит, логарифм числа 8 по основанию 2 будет равен 3. То есть:
log2 8 = 3
Пример 2: Решите уравнение log3 x = 2.
Решение:
Из определения логарифма по основанию 3 следует, что 3 возводится во вторую степень, чтобы получить число x. Таким образом, мы можем записать уравнение:
32 = x
После выполнения простого вычисления получаем, что x равно 9. Значит, решением уравнения будет:
x = 9
Пример 3: Найдите значение выражения log4 64 + log4 16.
Решение:
Сначала мы находим значения отдельных логарифмов:
log4 64 = 3, log4 16 = 2
Затем, мы суммируем эти значения:
3 + 2 = 5
Таким образом, значение выражения будет равно 5.



