Степени – это одна из важнейших математических операций, которая позволяет возводить число в определённую степень. Это значит, что мы можем умножить число само на себя несколько раз, указав число повторений – степень. Обычно степени представлены положительными целыми числами, но существуют и отрицательные и дробные степени.
Если степень отрицательна, то мы получаем обратное значение числа, возведённого в положительную степень. Например, чтобы возвести число 2 в степень -3, мы сначала возведем число в положительную степень (2 в степень 3), а затем возьмем обратное значение: 1 / (2 в степень 3) = 1 / 8 = 0.125.
Работа со степенями может быть немного сложнее, если степень является дробной. В этом случае мы используем понятие корня. Например, чтобы возвести число 9 в степень 1/2 (квадратный корень), мы найдем квадратный корень из числа 9, что равно 3.
Важно помнить, что работа со степенями, особенно с отрицательными и дробными степенями, требует внимательного подхода и тщательных вычислений. Неправильное использование степеней может привести к ошибкам и неправильным результатам. Поэтому необходимо внимательно проверять свои вычисления и использовать специальные математические функции или калькуляторы при необходимости.
Степени в математике

Степени могут быть как положительными, отрицательными, так и дробными. Положительные степени означают, что число умножается на самого себя несколько раз. Например, 23 равно 2 * 2 * 2 = 8.
Отрицательные степени означают, что число возводится в степень, обратную данной. Например, 2-3 равно 1 / (2 * 2 * 2) = 1/8.
Дробные степени означают, что число возводится в степень, которая является дробью. Например, 21/2 - квадратный корень числа 2, равный примерно 1.414.
При работе со степенями важно помнить некоторые правила:
- Степень числа 0 всегда равна 1: 0n = 1, где n ≠ 0;
- Любое число в степени 0 равно 1: a0 = 1, где a ≠ 0;
- Степень числа 1 всегда равна 1: 1n = 1;
- Степень 1/2 означает извлечение квадратного корня: a1/2 = √a;
- При умножении чисел с одинаковым основанием степень складывается: am * an = am+n;
- При делении чисел с одинаковым основанием степень вычитается: am / an = am-n;
- При возведении числа в степень, возведенное число можно умножить на само себя нужное количество раз: (am)n = am*n;
- Отрицательная степень числа равна обратной его положительной степени: a-n = 1 / an.
Что такое степень
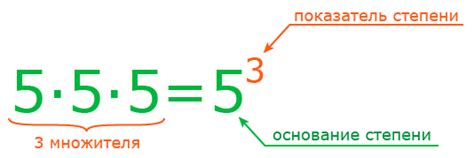
Степени могут быть как положительными, так и отрицательными. Положительная степень означает, что число умножается само на себя определенное количество раз, а отрицательная степень обратного числа означает, что число делится на само себя определенное количество раз.
Степени могут быть также и дробными. Дробная степень означает, что число умножается само на себя определенное количество раз, но возводится в корень с указанным знаменателем.
В математике степени имеют свои правила и законы. Например, умножение чисел со степенями с одинаковым основанием даёт степень с тем же основанием и суммой показателей степеней.
Работа со степенями

Степени представляют собой математический инструмент, который используется для обозначения повторных умножений числа на само себя. Работа со степенями может быть несколько сложнее, если они отрицательные или дробные.
Если степень отрицательная, то результат будет обратным числу, возведенному в положительную степень. Например, 2 в степени -3 будет равно 1/2 в кубе, то есть 1/8.
Если степень дробная, то результат можно представить как корень из числа. Например, 4 в степени 1/2 будет равно квадратному корню из 4, то есть 2.
Чтобы правильно работать со степенями, необходимо знать основные правила и свойства. Например, умножение чисел в степени с одним и тем же основанием равно сложению степеней: a^n * a^m = a^(n + m).
Также следует помнить о правиле возведения числа в степень 0, которое гласит, что любое число, кроме нуля, в степени 0 равно 1: a^0 = 1 (a ≠ 0).
Для удобства работы со степенями можно использовать калькулятор, который позволяет вводить числа и степени, а затем вычислять результат. Важно при этом следить за правильным вводом данных и проверять полученные результаты.
Правильное понимание работы со степенями позволяет решать различные задачи по алгебре и прикладным наукам. Овладев этими навыками, вы сможете более точно и эффективно решать различные математические задачи.
Как работать со степенями, если они отрицательные

| Ситуация | Расчет | Пример |
|---|---|---|
| Число в отрицательной степени | Возведение в степень и взятие обратного значения | 2-3 = 1 / (23) = 1 / 8 = 0.125 |
| Отрицательное число в положительной степени | Возведение в степень и взятие обратного значения | (-2)3 = -(23) = -8 |
| Отрицательное число в отрицательной степени | Возведение в степень, взятие обратного значения и добавление знака | (-2)-3 = 1 / ((-2)3) = 1 / (-8) = -0.125 |
Операции с отрицательными степенями требуют внимательности и точных расчетов, чтобы избежать ошибок. Важно помнить, что выполнение действий в правильной последовательности поможет получить правильные результаты.
Особенности работы со степенями в дробной форме

Работа со степенями чисел в дробной форме имеет свои особенности, которые следует учитывать при выполнении математических операций. Дробные степени часто встречаются в физических и экономических расчетах, а также в научных и инженерных задачах.
Когда степень отрицательна, число возводится в обратную степень, что эквивалентно делению единицы на это число, возведенное в положительную степень. Например, чтобы возвести число 2 в степень -1, нужно выполнить следующую операцию: 1/2^1 = 1/2 = 0.5. Если же степень отрицательная и число в основании равно нулю, то результатом будет бесконечность.
Для работы со степенями в дробной форме можно использовать формулу для вычисления общего случая: a^n/m = (a^1/m)^n.
Важно помнить, что числа в дробной степени можно записывать как иррациональные десятичные числа или как отношения двух целых чисел. В случае иррациональных десятичных чисел, вычисление степени может потребовать округления, что может сказаться на точности результата.
Еще одной особенностью работы со степенями в дробной форме является то, что возведение числа в дробную степень приводит к взятию корня из этого числа. Например, возвести число 4 в степень 1/2 (корень квадратный) эквивалентно извлечению квадратного корня из числа 4, что равно 2. Так же можно использовать работу со степенями как вычисление корня n-го порядка.
При работе со степенями в дробной форме также следует обратить внимание на возможность возникновения комплексных чисел в результате вычислений. Комплексное число получается, когда основание отрицательное и степень имеет нечетное значение. Например, (-1)^(1/3) = -1.
Примеры работы со степенями

Для понимания работы со степенями, давайте рассмотрим несколько примеров, включающих отрицательные и дробные показатели степени.
Пример 1: Отрицательные степени
Чтобы возвести число в отрицательную степень, нам нужно взять его обратное значение.
Например, если у нас есть число 2, и мы хотим возвести его в степень -3, то мы можем записать это как 1/23.
Таким образом, возводим в степень 3 и берем обратное значение, получая результат 1/8 или 0.125.
Пример 2: Дробные степени
Возводить число в дробную степень можно с помощью радикалов. Корень степени m из числа a может быть представлен в виде m√a.
Например, если мы хотим найти корень степени 2 из числа 4, это можно записать как 21/2.
Это означает, что мы ищем число, которое нужно возвести в квадрат, чтобы получить 4. В этом случае, корень из 4 равен 2.
Пример 3: Комбинированные степени
Мы также можем комбинировать отрицательные и дробные степени.
Например, если у нас есть число 3 и мы хотим возвести его в степень -1/2, мы можем записать это как 3-1/2.
Это означает, что мы ищем обратный корень квадратный из числа 3. В этом случае, извлечение обратного корня из 3 даст нам 1/√3.
Работая со степенями, важно помнить о правилах алгебры и использовать подходящие методы для решения задач.
Надеюсь, эти примеры помогли вам лучше понять, как работать со степенями, включая отрицательные и дробные показатели степени.
Практическое применение степеней

- Физика: Отрицательные степени используются для обозначения величин, обратных физическим величинам. Например, величина сопротивления в электрических цепях может быть выражена через отрицательную степень величины проводимости. Также, при решении задач в механике, дробные степени применяются при расчете площади поверхности объектов или объема тела.
- Экономика: Отрицательные и дробные степени широко используются при расчете процентов, скидок, налогов и других финансовых индикаторов. Например, при расчете суммы будущей платежной нагрузки или при определении стоимости использования кредита на протяжении определенного срока.
- Биология: Отрицательные степени применяются для работы с малыми числами. Например, при расчете концентрации растворов, массы микроорганизмов или концентрации гормонов в организме.
Это лишь несколько примеров областей, где применяются степени с отрицательными и дробными значениями. Знание правил и навыки работы с такими степенями помогают решать различные задачи, проводить научные исследования и анализировать данные.
Расширение применения степеней на практике

Отрицательные степени часто используются для обращения величин. Например, чтобы найти обратное значение числа, мы можем возвести его в отрицательную степень. К примеру, число 2 возводится в степень -1, получая в результате 1/2. Таким образом, величина, возведенная в отрицательную степень, становится обратной по отношению к исходной величине.
Дробные степени позволяют нам работать с корнями чисел. Квадратный корень числа можно представить как число, возведенное в степень 1/2. Например, квадратный корень из 4 равен 2, так как 2^2 = 4. Третья степень числа, также называемая кубическим корнем, представляет собой число, возведенное в степень 1/3. Например, кубический корень из 8 равен 2, так как 2^3 = 8.
Применение отрицательных и дробных степеней позволяет нам решать разнообразные задачи из различных областей. Например, в физике мы можем использовать степени для вычисления скорости, ускорения и сопротивления. В экономике степени помогают в рассчете процентных ставок и дисконтирования. Различные научные и инженерные дисциплины также широко используют степени в своих расчетах и моделях.



