Решение примеров – это задача, с которой сталкиваются все, начиная с учеников и заканчивая математиками. Не всегда легко разобраться с большими числами, сложными операциями и нестандартными задачами. Однако существуют алгоритмы и способы, которые помогут вам найти верное решение.
Среди них есть классические алгоритмы, такие как алгоритм Евклида для нахождения наибольшего общего делителя, алгоритм Дейкстры для поиска кратчайшего пути в графе, алгоритм Флойда–Уоршалла для нахождения всех кратчайших путей в графе и множество других. Эти алгоритмы часто используются в программировании и решении сложных математических проблем.
Кроме классических алгоритмов, существуют и другие способы, которые помогут вам решить пример. Например, алгоритм полного перебора позволяет проверить все возможные варианты решения и найти оптимальное. Алгоритм жадного выбора позволяет выбирать локально оптимальные решения на каждом шаге, что часто приводит к глобально оптимальному решению.
Таким образом, если вы столкнулись с задачей, которую головоломка для вас, не отчаивайтесь. Существует множество алгоритмов и способов, которые помогут вам найти правильное решение. При этом не забывайте использовать свою интуицию и логическое мышление, ибо они часто являются незаменимыми помощниками при решении сложных примеров.
Алгоритмы для решения примеров
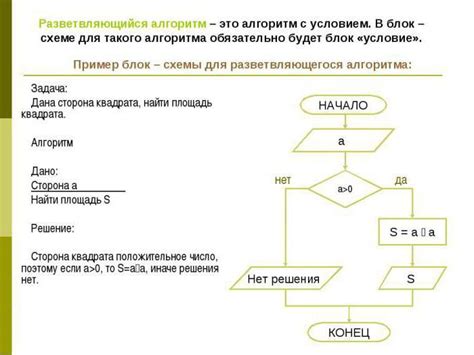
Решение математических примеров может быть вызовом для многих людей. Однако с помощью правильных алгоритмов и методов вы сможете справиться с этой задачей более легко и быстро.
Один из самых простых алгоритмов для решения примеров - это последовательность действий по порядку. Сначала выполняются умножение и деление, затем сложение и вычитание. Этот алгоритм позволяет избежать ошибок, связанных с приоритетностью операций.
Еще один полезный алгоритм - использование скобок для явного задания порядка действий. Скобки позволяют указать, какие операции необходимо выполнить в первую очередь и облегчают понимание выражения.
Если вы сталкиваетесь с примерами, содержащими сложные математические функции, такие как синус, косинус или корень, то может быть полезно использовать приближенные методы или таблицы значений для экономии времени.
Важной частью решения примеров является также работа с дробями и процентами. Для этого существуют специальные алгоритмы, которые помогут преобразовать числа и провести необходимые расчеты.
Независимо от примера, с которым вы столкнулись, важно помнить о том, что правильная последовательность действий и использование правильных алгоритмов является ключом к успешному решению примера. Не стесняйтесь использовать различные методы и техники для достижения желаемого результата. Упражнение делает мастера!
Не бойтесь примеров! Используйте различные алгоритмы для их решения и получайте удовольствие от математики!
Получение правильного решения

Не всегда легко найти правильное решение математического примера, особенно если он сложный или нестандартный. Однако, существуют различные алгоритмы, которые могут помочь вам найти правильный ответ.
Один из таких алгоритмов – алгоритм последовательности действий. С его помощью вы можете разбить сложный пример на несколько более простых шагов и решить их поочередно. Это позволит вам избежать ошибок и получить верное решение исходной задачи.
Еще одним полезным алгоритмом является алгоритм применения приоритетов. Он позволяет определить, какие операции должны быть выполнены в первую очередь, а какие – во вторую. Например, умножение и деление имеют более высокий приоритет перед сложением и вычитанием. Правильное применение приоритетов операций поможет получить правильный результат.
Если вам сложно найти правильное решение примера, вы также можете воспользоваться алгоритмом проверки. С его помощью вы можете проверить свое решение, подставив его обратно в задачу и убедившись, что получите правильный ответ. Если результат верный, значит вы на правильном пути. Если нет, необходимо попробовать другие методы и алгоритмы для нахождения правильного решения.
Важно помнить, что математика – это наука, требующая логики и точности. Поэтому при использовании алгоритмов для нахождения правильного решения важно внимательно прочитывать задачу, учитывать условия и правила математики, чтобы избежать ошибок и получить правильный результат.
Преимущества использования алгоритмов

Алгоритмы играют ключевую роль в решении различных задач и проблем, включая решение математических примеров. Их использование имеет множество преимуществ, которые делают их неотъемлемой частью нашей повседневной жизни.
- Точность: Алгоритмы работают на основе логики и стройной последовательности шагов, что позволяет добиться высокой точности в решении задач. Это особенно важно в математике, где даже небольшие ошибки могут привести к неправильным ответам.
- Эффективность: Использование алгоритмов позволяет сократить время на решение сложных задач. Благодаря определенной структуре и последовательности действий, алгоритмы могут быть оптимизированы для достижения максимальной эффективности.
- Универсальность: Алгоритмы могут быть применены к широкому спектру задач и проблем. Они не ограничены только математическими вычислениями, а также находят применение в компьютерных науках, медицине, финансах и других областях.
- Репродуцируемость: Алгоритмы могут быть записаны и переданы другим людям или использованы повторно в различных ситуациях. Это позволяет достичь консистентности и надежности в решении задач.
- Поддержка принятия решений: Алгоритмы могут стать полезным инструментом при принятии решений. Они могут помочь разбить сложную задачу на более простые подзадачи, а также предоставить систематический и логический подход к принятию решений.
Использование алгоритмов имеет множество преимуществ и позволяет нам решать задачи более эффективно и точно. Независимо от того, нужно ли нам решить математический пример или решить более сложную проблему, алгоритмы могут быть надежным инструментом для достижения успеха.
Популярные алгоритмы для решения примеров
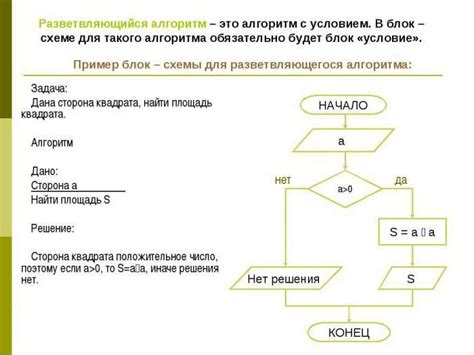
При решении математических примеров возможно применение различных алгоритмов, которые помогут найти правильное решение. В этом разделе мы рассмотрим несколько популярных алгоритмов:
- Алгоритм сложения - основа для решения примеров, требующих сложения чисел. Он заключается в пошаговом складывании цифр, начиная справа.
- Алгоритм вычитания - позволяет решить примеры, где требуется вычитание чисел. Он также работает пошагово, начиная справа и перенося разряды при необходимости.
- Алгоритм умножения - используется, когда необходимо умножить два числа. Он основан на пошаговом перемножении цифр и последующем сложении полученных произведений.
- Алгоритм деления - помогает решить примеры, где требуется разделить одно число на другое. Этот алгоритм основан на пошаговом вычитании и определении остатка.
Кроме того, существует множество других алгоритмов, которые помогают решать более сложные примеры и задачи, включая алгоритмы возведения в степень, нахождения корней, решения уравнений и другие. Поиск и использование подходящего алгоритма может значительно упростить решение примера и помочь получить правильный ответ.
Надеемся, что этот раздел поможет вам разобраться в различных алгоритмах и выбрать тот, который наиболее подходит для решения вашего примера.
Выбор наиболее подходящего алгоритма

Первым шагом в выборе алгоритма является определение типа примера. Например, если тебе нужно произвести сложение или вычитание чисел, то наиболее подходящим алгоритмом будет арифметический алгоритм. Если же задача связана с умножением или делением, то можно использовать алгоритмы умножения или деления соответственно.
Вторым шагом является оценка сложности примера. Если у тебя есть возможность выбора между алгоритмами, имеющими различную сложность, нужно выбрать тот, который будет быстрее решать пример. Например, для простых примеров можно использовать простые алгоритмы, а для более сложных - более сложные алгоритмы.
Третьим шагом является сравнение эффективности алгоритмов. Некоторые алгоритмы могут работать быстрее или потреблять меньше ресурсов, чем другие. Поэтому, прежде чем приступить к решению примера, нужно сравнить различные алгоритмы и выбрать наиболее эффективный.



