Математика полна интересных и сложных концепций, одной из которых является возведение числа в степень. В большинстве случаев мы привыкли работать с положительными степенями, такими как 2 в квадрате или 10 в третьей степени. Однако, что происходит, когда число возводят в степень, равную минус бесконечности?
Выражение "число в степени минус бесконечность" может показаться загадочным или нелогичным, но на самом деле оно имеет строгое математическое определение и результат. Когда число возводится в отрицательную бесконечность, это означает, что мы рассматриваем предел функции этого числа при приближении аргумента к минус бесконечности.
Результат возведения числа в степень минус бесконечность может быть различным в зависимости от самого числа. Например, если число равно 1, результат будет равен 1. Однако для большинства чисел результат будет различным и зависеть от их свойств. Эта концепция имеет важное значение в анализе функций и математическом моделировании, где возникают ситуации, когда аргументы стремятся к минус бесконечности.
Число в степени минус бесконечность: что это значит и каков результат
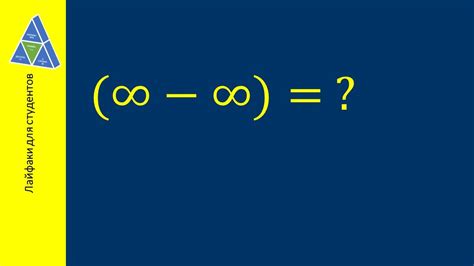
Математика знакома нам с различными операциями и действиями с числами. Однако, когда речь идет о числе, возведенном в степень минус бесконечность, многие начинают задаваться вопросами относительно смысла и результата такой операции.
При обычной операции возведения числа в определенную степень мы умножаем число само на себя столько раз, сколько указано в степени. Но что происходит, когда степень равна минус бесконечности?
В данном случае, результат операции зависит от самого числа. Если основание степени является положительным числом, то результат будет равен нулю. Например, 2 в степени минус бесконечность равно 0.
Если основание степени является отрицательным числом, то результат операции будет зависеть от четности степени. Если степень является нечетной, то результат будет равен минус бесконечности. Например, (-3) в степени минус бесконечность равно минус бесконечность. В то же время, если степень является четной, то результат будет равен плюс бесконечности. Например, (-2) в степени минус бесконечность равно плюс бесконечности.
Итак, число в степени минус бесконечность может принимать различные значения в зависимости от самого числа. Это является важным аспектом при решении математических задач и анализе функций.
Понятие степени и бесконечности в математике

Когда мы говорим о числе в степени минус бесконечность, мы вводим понятие предела. Предел - это концепция, которая определяет, какое значение подходит к числу, когда независимая переменная стремится к определенной точке. В случае степени минус бесконечность, мы рассматриваем, что происходит с числом, когда показатель степени стремится к минус бесконечности.
При рассмотрении числа в степени минус бесконечность два случая могут произойти. Если число меньше 1, то оно будет стремиться к бесконечности, так как при умножении на самого себя оно будет увеличиваться с каждым шагом. Например, число 1/2 возводится в степень -∞ даст результат 0, так как оно будет уменьшаться с каждым умножением: (1/2)-∞ = 1/(2∞) = 1/бесконечность = 0.
Если число больше 1, то оно будет стремиться к нулю, так как каждое умножение на самого себя делает его все меньше. Например, число 2 возводится в степень -∞ даст результат 0, так как оно будет уменьшаться с каждым умножением: 2-∞ = 1/(2∞) = 1/бесконечность = 0.
| Число | Результат |
|---|---|
| Число меньше 1 | 0 |
| Число больше 1 | 0 |
Таким образом, число в степени минус бесконечность стремится к 0 в математике, вне зависимости от того, является ли число больше или меньше 1.
Число в степени минус бесконечность: определение и свойства

Когда число возводится в степень минус бесконечность, его значение зависит от типа числа и правил операций над этим числом.
Определение и свойства числа в степени минус бесконечность:
| Тип числа | Результат |
|---|---|
| Положительное число | Равно нулю, если основное число не равно единице |
| Отрицательное число | Не определено |
| Нуль | Равно единице, кроме случая 0^(-∞) |
| Единица | Равно единице |
В случаях, когда основное число положительное, его значение в степени минус бесконечность будет стремиться к нулю. Это связано с тем, что при возведении большого положительного числа в очень маленькую отрицательную степень, результат будет близким к нулю.
Если основное число отрицательное, то значение в степени минус бесконечность не определено. Это связано с тем, что при возведении отрицательного числа в отрицательную степень мы получаем комплексные числа, которые не имеют физического смысла.
Если основное число равно нулю, то значение в степени минус бесконечность будет равно единице, за исключением случая 0^(-∞), который не имеет определенного значения.
Если основное число равно единице, то значение в степени минус бесконечность будет равно единице. Это связано с тем, что при любой отрицательной экспоненте единица остается неизменной.
Число в степени минус бесконечность: расчеты и примеры

Если число a больше 1, то a-∞ равно 0. Это можно интерпретировать следующим образом: при увеличении значения x отрицательной бесконечностью, функция ax стремится к нулю. Например, 2-∞ = 0.
Если число a меньше 1, то a-∞ равно плюс бесконечности, то есть a-∞ = ∞. Это может быть объяснено следующим образом: при увеличении значения x отрицательной бесконечностью, функция ax растет неограниченно. Например, 0.5-∞ = ∞.
Если a равно 1, то a-∞ является неопределенным. В этом случае результат зависит от контекста и не может быть однозначно определен.
Для наглядности рассмотрим примеры вычислений:
- 2-∞ = 0
- 0.5-∞ = ∞
- 1-∞ = неопределенный результат
Важно отметить, что использование числа в степени минус бесконечность не всегда встречается в математических задачах. Это понятие чаще используется в теории пределов и при изучении аналитической геометрии. В практических вычислениях обычно используются другие подходы и инструменты.
Число в степени минус бесконечность: граничные случаи и особенности
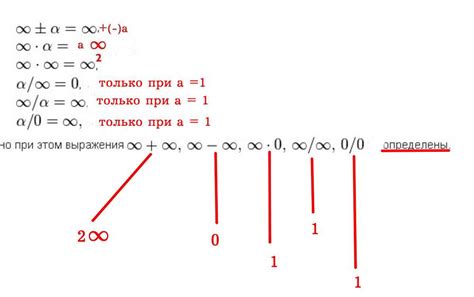
| Определение | Значение |
|---|---|
| Число > 0 | Результат стремится к 0 |
| Число = 0 | Результат стремится к 1 |
| Число | Результат зависит от четности степени: при четной степени результат стремится к 0, при нечетной - к ± бесконечности (знак зависит от знака числа) |
| Число | Результат не определен |
Чтобы более точно понять, что происходит при возведении числа в степень минус бесконечность, необходимо учитывать указанные граничные случаи и особенности. Также стоит отметить, что каждая математическая система может иметь свои особенности и правила расчета таких степеней. Поэтому важно дополнительно ознакомиться с правилами математического контекста, в котором будет применяться данная операция.
Число в степени минус бесконечность: пределы и асимптоты

Когда число возводится в степень минус бесконечность, результат зависит от значения самого числа и может принимать разные формы. Рассмотрим несколько случаев:
1. Если число, возводимое в степень, равно нулю:
0 в степени минус бесконечность обозначается как 0^(-∞). В этом случае результатом будет нуль, так как любое число, не равное нулю, возводимое в отрицательную бесконечность, стремится к нулю.
2. Если число, возводимое в степень, положительное и больше единицы:
Пусть a - положительное число, большее единицы. Тогда a^(-∞) будет стремиться к нулю. В этом случае можно сказать, что функция, заданная выражением a^x, имеет асимптоту y=0 при x, стремящемся к минус бесконечности.
3. Если число, возводимое в степень, отрицательное и меньше единицы:
Пусть a - отрицательное число, меньшее единицы. Тогда a^(-∞) будет стремиться к положительной бесконечности или иметь предел бесконечности. В этом случае можно сказать, что функция, заданная выражением a^x, имеет асимптоту y=∞ или y=-∞ при x, стремящемся к минус бесконечности.
Таким образом, число в степени минус бесконечность может иметь различные пределы и асимптоты в зависимости от значения самого числа. Это понятие играет важную роль в анализе функций и в других областях математики, позволяя более точно описывать их свойства и поведение в пределах бесконечности.
Число в степени минус бесконечность: приложения в науке и технике
Число в степени минус бесконечность представляет собой математическую концепцию, которая имеет важное значение в различных областях науки и техники. Это выражение возникает, когда число возводится в отрицательно бесконечную степень, то есть когда показатель степени стремится к отрицательной бесконечности.
Результат выражения числа в степени минус бесконечность может быть разным в зависимости от самого числа и используемой математической функции. Однако, в большинстве случаев, результатом будет нуль или бесконечность.
В науке и технике применение числа в степени минус бесконечность встречается в различных областях. Например, в математике такое выражение может использоваться при решении разностных уравнений или в задачах оптимизации. Также, в физике такое выражение может встречаться в уравнениях, описывающих электрические и магнитные поля, кинетику исчезающих процессов, а также в задачах распределения вероятностей.
Пример приложения числа в степени минус бесконечность в науке:
Пусть у нас есть задача моделирования процесса зарядки и разрядки конденсатора в электрической схеме. В таком случае, для описания зарядки конденсатора мы можем использовать уравнение:
I(t) = I0 * exp(-t/RC)
где I(t) - ток, протекающий через конденсатор в момент времени t, I0 - начальный ток, R - сопротивление и C - емкость конденсатора. Если мы хотим исследовать, что произойдет со значением тока в момент времени, бесконечно удаленном в прошлое, то есть (t → -∞), мы можем воспользоваться числом в степени минус бесконечность:
lim(I(t) при t → -∞) = lim(I0 * exp(-t/RC) п r t → -∞) = 0
Таким образом, приложение числа в степени минус бесконечность в данной задаче позволяет определить, что ток через конденсатор в момент времени, бесконечно удаленном в прошлое, стремится к нулю.
Использование чисел в степени минус бесконечность в науке и технике помогает моделировать и анализировать различные процессы, решать уравнения и оптимизационные задачи. Это важный инструмент в исследовании и развитии науки и техники.
Число в степени минус бесконечность: отрицательная бесконечность и результат
Когда число возведено в степень минус бесконечность, это означает, что степень стремится к отрицательной бесконечности. Такая ситуация возникает, когда значение степени с каждым шагом уменьшается до отрицательной бесконечности.
Результат возведения числа в степень минус бесконечность зависит от самого числа. Если число равно единице, то результат будет равен единице, независимо от знака степени. Это можно выразить следующим образом: 1-∞ = 1.
Если число больше единицы, то результат будет равен нулю, когда степень стремится к минус бесконечности: a-∞ = 0, где a > 1. Это связано с тем, что при увеличении степени, числитель стремится к константе, тогда как знаменатель стремится к бесконечности, и их отношение будет стремиться к нулю.
Если же число находится в интервале от нуля до единицы, то результат возведения в степень минус бесконечность будет бесконечно большим числом: a-∞ = ∞, где 0 . Это связано с тем, что при увеличении степени, знаменатель стремится к нулю, а числитель остается постоянным, и их отношение будет стремиться к бесконечности.
Важно знать, что возведение числа в степень минус бесконечность не является определенной операцией и результат зависит от самого числа. Поэтому необходимо быть осторожным при использовании таких выражений и учитывать их математическую особенность.
Число в степени минус бесконечность: положительная бесконечность и результат

Число в степени минус бесконечность возникает при рассмотрении пределов функций или математических выражений с переменной.
Когда число возведено в степень минус бесконечность, результат может быть двумя вариантами - положительная бесконечность или значение, равное нулю.
- 1. Положительная бесконечность:
- 2. Результат, равный нулю:
Если положительное число возведено в степень минус бесконечность, результатом будет положительная бесконечность. Например, 2 в степени минус бесконечность равно бесконечности.
Если число, меньшее единицы, возведено в степень минус бесконечность, результатом будет значение, равное нулю. Например, 0.5 в степени минус бесконечность равно нулю.
Когда указывается число в степени минус бесконечность, существует строгий математический алгоритм для определения результата. Поэтому важно ставить правильные условия и учесть возможные исключения в выражениях.
Число в степени минус бесконечность: нуль и результат

Существует несколько случаев, когда число возведённое в степень минус бесконечность может иметь конкретное значение или результат:
Если число больше единицы, то при возведении в степень минус бесконечность результатом будет ноль. Например, 2 в степени минус бесконечность будет равно 0, так как при бесконечном возведении в степень число будет стремиться к бесконечно малому значению, а это ноль.
Если число меньше единицы, то при возведении в степень минус бесконечность результатом будет бесконечность. Например, 0.5 в степени минус бесконечность будет равно бесконечности, так как при бесконечном возведении в степень число будет стремиться к бесконечно большому значению.
Если число равно единице, то при возведении в степень минус бесконечность результатом будет неопределенность. Например, 1 в степени минус бесконечность не имеет определенного значения, так как при бесконечном возведении в степень число будет колебаться и не сойдется к одному конкретному значению.
Таким образом, результат возведения числа в степень минус бесконечность зависит от самого числа и может быть равен нулю, бесконечности или быть неопределенным.



