Алгебра – это одна из основных разделов математики, изучающая алгебраические структуры и операции над ними. В алгебре используются различные символы и обозначения, и иногда встречается число в скобках. Что означает число, заключенное в скобки, и как его следует интерпретировать?
Число в скобках в алгебре может иметь разные значения в зависимости от контекста. Во-первых, оно может обозначать операцию умножения. Например, в выражении (a + b) * c число в скобках указывает на то, что необходимо сначала выполнить операцию сложения a + b, а затем умножить полученную сумму на число c.
Во-вторых, число в скобках может быть использовано для группировки символов и обозначения порядка выполнения операций. Например, в выражении a + (b * c) число в скобках указывает, что необходимо сначала выполнить умножение символов b и c, а затем прибавить полученное произведение к символу a.
Число в скобках может использоваться и для обозначения условия, при котором выполнение операции обязательно. Например, в выражении a * (b + c) число в скобках может означать, что перед выполнением операции умножения символов a и (b + c) необходимо выполнить сложение символов b и c.
Основные понятия в алгебре
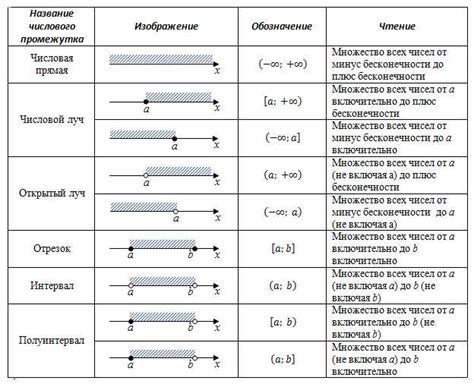
В алгебре важным понятием является число. Числа в алгебре могут быть натуральными, целыми, рациональными, иррациональными или комплексными. Натуральные числа – это положительные целые числа, начиная от единицы. Целые числа включают натуральные числа, нуль и отрицательные числа. Рациональные числа представляются дробью, где числитель и знаменатель являются целыми числами. Иррациональные числа не могут быть представлены дробью, например, корень квадратный из числа 2. Комплексные числа состоят из действительной и мнимой частей.
Операции – это действия над числами, такие как сложение, вычитание, умножение и деление. Они позволяют осуществлять математические операции и решать уравнения. Алгебра использует символы и переменные для обозначения неизвестных величин. Уравнения в алгебре представляют собой равенства, включающие неизвестные и известные числа. Графики функций позволяют визуально представить алгебраические уравнения и анализировать свойства функций.
Решение уравнений и построение графиков функций являются основными задачами алгебры. Они позволяют решать множество практических задач, связанных с моделированием и анализом данных. Знание основных понятий в алгебре является важным для понимания и применения математических методов в различных областях знаний, включая физику, экономику и информатику.
Значение числа в алгебре и его роль в выражениях

Значение числа в алгебре отражает его величину или свойство. Например, если у нас есть выражение 2 + 3, число 2 и число 3 имеют свое значение, которое определяет их сумму в данном выражении. Значение чисел может быть как положительным, так и отрицательным, и это также оказывает влияние на значение всего выражения.
Роль чисел в выражениях заключается в их вкладе в итоговый результат. Каждое число выполняет определенную операцию, в зависимости от знака операции и положения числа в выражении. Например, в выражении 2 * 3, число 2 является множителем, а число 3 - другим множителем. Их значение и роль определяют результат умножения.
Числа в алгебре могут иметь различное значение в разных контекстах. Например, в уравнениях числа могут представлять неизвестные величины, которые ищутся в ходе решения. Они могут быть обозначены буквами, такими как x или y, и их значения находятся в результате алгебраических операций.
Важно понимать значение чисел в алгебре, чтобы правильно составлять выражения и решать уравнения. Значение чисел влияет на результаты операций и их взаимодействие в алгебраических выражениях. Правильное определение значений чисел помогает получить верные ответы и точные результаты в алгебре.
Знак числа в алгебре и его влияние на результат

Знак числа также имеет влияние на результат выполнения алгебраических операций. Вот некоторые примеры:
- Сложение: при сложении чисел разных знаков, результат будет иметь знак числа с большей по абсолютной величине. Например, -3 + 5 = 2.
- Вычитание: при вычитании чисел разных знаков, знак числа, от которого вычитают, сохраняется. Например, -8 - 3 = -11.
- Умножение: при умножении чисел разных знаков, результат всегда будет отрицательным числом. Например, -2 * 7 = -14.
- Деление: при делении двух чисел с разными знаками, результат всегда будет отрицательным числом. Например, -18 / 3 = -6.
Знак числа также играет роль при решении уравнений и неравенств. Например, при умножении или делении уравнения на отрицательное число, знак неравенства меняется.
Важно помнить, что знак числа - это важный аспект в алгебре, который влияет на результат алгебраических операций и решения уравнений. Поэтому при работе с числами в алгебре всегда необходимо учитывать их знак и правильно выполнять операции с числами разных знаков.
Возведение числа в степень и его значение

Возведение числа в степень широко применяется в различных областях, таких как физика, экономика, информатика и другие. Знание этой операции позволяет производить расчеты и получать решения в более удобной форме.
Значение числа, возведенного в степень, определяется путем умножения этого числа на самого себя заданное количество раз. Например, числу 2 в степени 3 соответствует произведение 2 * 2 * 2 = 8.
Для удобства математики существует терминология, которая помогает определить свойства возведения числа в степень:
| Термин | Определение |
|---|---|
| Основание степени | Число, которое возводится в степень |
| Показатель степени | Число, указывающее, сколько раз нужно умножить основание степени на себя |
| Значение степени | Результат возведения основания степени в заданный показатель |
При возведении положительного числа в отрицательную степень, получается десятичная дробь или число с плавающей запятой. Например, 2 в степени -2 равно 1/2 * 1/2 = 1/4.
Возведение числа в нулевую степень всегда дает единицу. Это связано с определением степени и множителей.
При возведении единицы в любую степень, результат всегда будет равен единице. Это свойство обосновывается с помощью базовых свойств арифметических операций.
Возведение нуля в любую положительную степень дает ноль. Это свойство следует из базовых законов арифметики.
Корень числа и его значимость в алгебре

Корни чисел являются важными в алгебре, так как они позволяют решать множество уравнений и задач. Корни чисел используются, например, для нахождения значений переменных в квадратных уравнениях или для вычисления длины сторон в геометрии.
Значение числа в скобках, обозначающих корень, также играет важную роль. Оно указывает на степень корня и определяет, сколько раз нужно возвести число в эту степень, чтобы получить исходное значение. Например, если значение числа в скобках равно 2, то это значит, что требуется возвести число в квадратный корень.
Знание корней чисел и понимание их значимости в алгебре является необходимым для решения различных математических задач. Умение находить корни и использовать их в вычислениях позволяет упростить и ускорить процесс решения задач и уравнений.
Операции над числами и их значение в математике
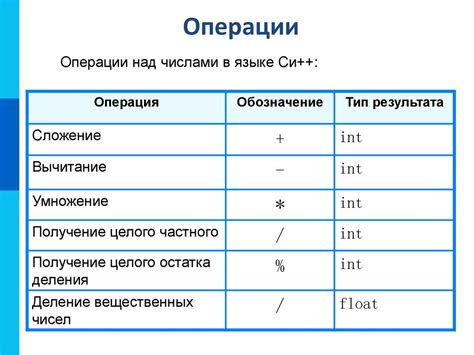
В математике существуют четыре основных операции над числами: сложение, вычитание, умножение и деление. Каждая из этих операций имеет свое значение и используется для различных целей.
| Операция | Знак | Значение |
|---|---|---|
| Сложение | + | Сложение двух чисел дает сумму этих чисел. Например, 2 + 3 = 5. |
| Вычитание | - | Вычитание одного числа из другого дает разность этих чисел. Например, 5 - 2 = 3. |
| Умножение | * | Умножение двух чисел дает произведение этих чисел. Например, 2 * 3 = 6. |
| Деление | / | Деление одного числа на другое дает отношение этих чисел. Например, 6 / 2 = 3. |
Значение числа в скобках в алгебре может означать различные вещи в зависимости от контекста. Например, в выражении (2 + 3) * 4, число в скобках означает, что сначала необходимо выполнить операцию в скобках (2 + 3), а затем результат умножить на 4. Таким образом, результат выражения будет равен 20.
Знание операций над числами и их значения позволяет нам решать математические задачи, проводить вычисления и анализировать данные. Эти знания также имеют практическое применение в повседневной жизни, помогая нам считать деньги, делать покупки, строить графики и многое другое.
Функции и их значение для чисел в алгебре

В алгебре функции играют важную роль в определении значения чисел. Функции можно рассматривать как специальные правила, которые преобразуют одно число в другое.
Одной из основных функций, используемых в алгебре, является функция возведения в степень. Эта функция позволяет умножить число на само себя несколько раз. Например, функция "возведение в квадрат" преобразует число в результат его умножения на само себя:
Функция возведения в квадрат: x2
Здесь число x является аргументом функции, и результатом выполнения этой функции будет число, полученное путем умножения x на само себя.
Еще одной важной функцией в алгебре является функция извлечения корня. Эта функция позволяет найти число, которое, возведенное в заданную степень, равно заданному числу. Например, функция "корень квадратный" преобразует число в результат его возведения в квадрат:
Функция корень квадратный: √x
Здесь число x является аргументом функции, и результатом выполнения этой функции будет число, возведение которого в квадрат равно x.
Одной из самых простых функций в алгебре является функция идентичности. Эта функция просто возвращает значение аргумента, то есть результатом выполнения функции будет само число:
Функция идентичности: f(x) = x
Здесь число x является аргументом функции, и результатом выполнения этой функции будет само число x.
Таким образом, функции в алгебре играют важную роль в определении значения чисел. Путем применения различных функций, мы можем изменять числа и получать новые результаты.
Число в квадратных скобках: как его интерпретировать в алгебре

Число, заключенное в квадратные скобки, в алгебре имеет особое значение и обозначается как [x]. Этот символ часто используется в контексте векторов или матриц, и интерпретация его значения зависит от конкретного контекста.
В контексте векторов, число в квадратных скобках обозначает компоненту вектора по определенной оси или направлению. Например, если имеется вектор [x, y], то [x] будет обозначать компоненту вектора по горизонтальной оси, а [y] - компоненту по вертикальной оси.
В контексте матриц, число в квадратных скобках указывает на элемент матрицы. Каждый элемент матрицы может быть представлен в виде матричного уравнения [a_{ij}], где [i] - номер строки, а [j] - номер столбца элемента.
Также, число в квадратных скобках может иметь и другие значения в зависимости от специфики задачи или символики, используемой в алгебре. Например, в некоторых книгах и статьях, число в квадратных скобках может обозначать округление числа или факториал. Поэтому, важно учитывать контекст и пояснения, которые предоставлены в условии задачи или определении символов.
Значение числа в круглых скобках и его особенности

Когда в алгебре встречается число, заключенное в круглые скобки, это указывает на необходимость выполнить определенные действия с числом.
Основной принцип использования чисел в скобках заключается в том, чтобы сначала выполнить операции с числами в скобках, а затем провести остальные действия с остальной частью выражения. Например, если в выражении есть число (3 + 4) * 2, сначала нужно выполнить операцию в скобках, то есть сложить 3 и 4, а затем умножить полученную сумму на 2.
Еще одна особенность чисел в скобках заключается в том, что скобки могут использоваться для указания порядка выполнения действий в сложных выражениях. Например, если имеется выражение 2 * (3 + 4), операция в скобках будет выполнена первой, а затем полученное значение будет умножено на 2.
Участие числа в скобках в алгебре существенно влияет на значение выражения. Важно всегда учитывать правила выполнения действий с числами в скобках и не пропускать этот шаг при решении математических задач.



