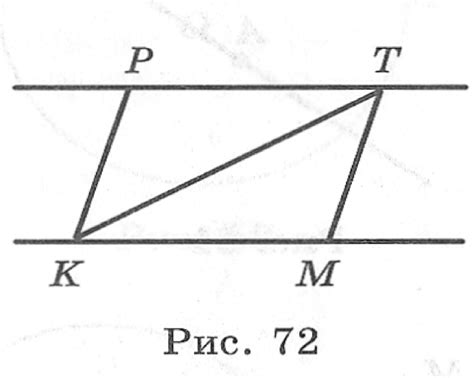
Трапеция - это одна из наиболее распространенных геометрических фигур, которую мы изучаем в школе. Она обладает некоторыми особыми свойствами. Однако, не все четырехугольники сразу могут считаться трапециями. Существуют определенные правила и условия, которым должен соответствовать четырехугольник, чтобы считаться трапецией.
Четырехугольник abcd не является трапецией, потому что у него отсутствует одно из основных условий. Для того чтобы четырехугольник считался трапецией, две его стороны должны быть параллельны и никакие две другие стороны не должны быть параллельны. В нашем случае, стороны ab и cd могут быть параллельны, но стороны ad и bc также являются параллельными. Это нарушает условие трапеции и делает четырехугольник abcd неподходящим для этой категории.
Следовательно, чтобы четырехугольник был трапецией, необходимо чтобы у него было минимум две параллельные стороны и остальные две стороны должны быть не параллельны друг другу. Это условие не выполняется для четырехугольника abcd, поэтому мы не можем назвать его трапецией.
Нарушение свойства равных углов
Углы ab и cd этого четырехугольника являются неравными, поскольку находятся в разных полуплоскостях отрезка ac. То есть, они лежат по разные стороны от прямой ac и могут принимать различные значения. Вместе с тем, в трапеции углы ab и cd всегда равны.
Таким образом, несоблюдение свойства равных углов является основным признаком, позволяющим отличить четырехугольник abcd от трапеции.
Углы a и d не равны друг другу
Данный четырехугольник не может являться трапецией, так как его углы a и d не равны друг другу.
Трапеция - это четырехугольник, у которого две стороны параллельны, называемые основаниями, и две другие стороны непараллельны, называемые боковыми сторонами. Углы при основаниях трапеции смежные и равны между собой, в то время как углы между боковыми сторонами и основаниями трапеции противоположные и также равны.
a | b |
c | d |
Нарушение свойства параллельных сторон
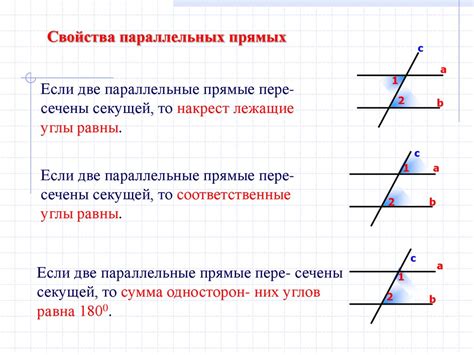
В трапеции одна пара сторон всегда параллельна, а другая пара - нет. В случае с четырехугольником abcd, какое бы расположение точек a, b, c и d мы не рассмотрели, мы не сможем найти такую пару параллельных сторон, так как все они могут быть не параллельны друг другу.
Параллельные стороны в трапеции имеют одинаковую длину или делятся определенным отношением, а в четырехугольнике abcd такого свойства не наблюдается.
Стороны ab и cd не параллельны друг другу