Равнобедренный прямоугольный треугольник является одним из самых интересных и независимых объектов в геометрии. Каждый равнобедренный прямоугольный треугольник имеет два равных катета и прямой угол между ними. Эти катеты являются основными элементами треугольника и определяют его свойства и характеристики.
Равнобедренный прямоугольный треугольник обладает уникальными особенностями. Как уже было сказано, его два катета являются равными и прямыми. Это означает, что в таком треугольнике две стороны, прилегающие к прямому углу, имеют одинаковую длину. В то же время, третья сторона, являющаяся гипотенузой, отличается от катетов.
Легко вывести выражение, которое выражает катеты через гипотенузу. По теореме Пифагора, сумма квадратов катетов равна квадрату гипотенузы. В равнобедренном прямоугольном треугольнике это выражение принимает вид a^2 + a^2 = c^2, где a - длина каждого катета, c - длина гипотенузы.
Определение равнобедренного прямоугольного треугольника
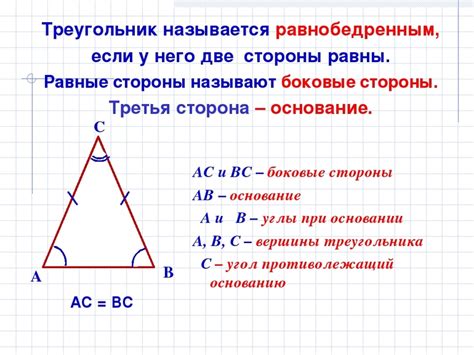
В равнобедренном прямоугольном треугольнике, катеты - это две равные стороны, которые образуют прямой угол. Для такого треугольника верно, что длина катетов равна.
Зная длину одного катета, можно рассчитать длину другого катета с использованием теоремы Пифагора.
Согласно теореме Пифагора, сумма квадратов длин катетов равна квадрату гипотенузы: a^2 + b^2 = c^2, где a и b - длины катетов, а c - длина гипотенузы.
Таким образом, в равнобедренном прямоугольном треугольнике катеты равны друг другу и равны длине гипотенузы, деленной на √2: a = b = c/√2.
Свойства равнобедренного прямоугольного треугольника
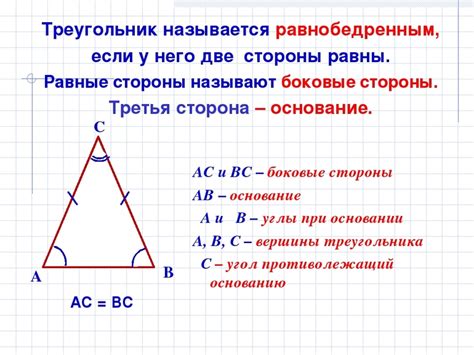
Катеты в равнобедренном прямоугольном треугольнике равны между собой и обозначаются буквой c. Он является прямым углом, а его длина определяется по теореме Пифагора: c² = a² + b², где a и b - длины катетов.
Таким образом, в равнобедренном прямоугольном треугольнике оба катета равны между собой и равны квадратному корню из суммы их квадратов.
Формула для расчета катетов
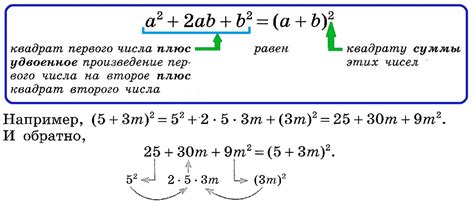
Для расчета величины катетов в равнобедренном прямоугольном треугольнике можно использовать следующую формулу:
| Строение формулы | Обозначение | Пример расчета |
|---|---|---|
| Катет | a или b | a = b = c/√2 |
| Гипотенуза | c | c = a√2 = b√2 |
Где a и b – длины катетов, c – длина гипотенузы.
Таким образом, если известна длина гипотенузы, можно расчитать длину катетов при помощи данной формулы. Обратно, зная длины катетов, можно определить длину гипотенузы.
Примеры использования формулы

Давайте рассмотрим несколько примеров использования формулы для вычисления длины катетов в равнобедренном прямоугольном треугольнике.
Пример 1:
- Известно, что гипотенуза равна 10 см.
- Используем формулу: катет = гипотенуза / √2
- Подставляем известные значения: катет = 10 / √2 ≈ 7.07 см
Пример 2:
- Известно, что один из катетов равен 6 см.
- Используем формулу: гипотенуза = катет * √2
- Подставляем известные значения: гипотенуза = 6 * √2 ≈ 8.48 см
Пример 3:
- Известно, что площадь треугольника равна 24 квадратных сантиметра.
- Используем формулу: катет = √(площадь треугольника / 2)
- Подставляем известные значения: катет = √(24 / 2) ≈ 4.90 см
Таким образом, формула позволяет легко и быстро вычислять длины катетов в равнобедренном прямоугольном треугольнике при известных значениях гипотенузы, одного из катетов или площади треугольника. Это полезное знание при решении геометрических задач и вычислении размеров объектов.



