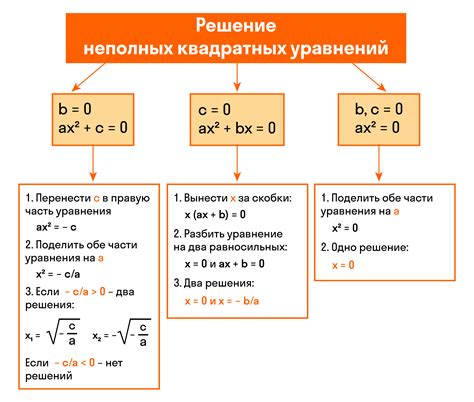
Квадратное уравнение – это уравнение вида ax^2 + bx + c = 0, где a, b и c – коэффициенты, причем a ≠ 0. Решение квадратного уравнения может быть представлено в виде формулы дискриминанта, которая позволяет найти значения переменной x. Однако, что делать, если у нас имеется только один из коэффициентов или некоторые из этих коэффициентов равны нулю?
Если в уравнении отсутствует коэффициент b (т.е. b = 0), то мы имеем дело с неполном квадратном уравнением. В таком случае, уравнение принимает следующий вид: ax^2 + c = 0. Для нахождения значения переменной x необходимо применить формулу дискриминанта, приведя уравнение к стандартной форме.
Значение дискриминанта такого неполном квадратного уравнения легко найти, используя формулу: D = b^2 - 4ac. При этом, значение переменной x можно найти посредством простой подстановки, заменив в уравнении c на -D.
Понятие неполного квадратного уравнения

Если отсутствует коэффициент при x^2 (a = 0), уравнение становится линейным. Если отсутствует коэффициент при x (b = 0), уравнение становится квадратным. Если отсутствует свободный член (c = 0), уравнение становится однородным.
Решение неполного квадратного уравнения можно найти с использованием различных методов, таких как метод Феррари, метод подстановки, метод дополнительных выражений и т.д. Из-за отсутствия некоторых коэффициентов, неполные квадратные уравнения могут иметь специфические свойства и требовать индивидуального подхода к решению.
Значение переменной в неполном квадратном уравнении зависит от значений коэффициентов a, b и c. Чтобы найти корни уравнения, необходимо решить квадратное уравнение, полученное после приведения неизвестной переменной к одной степени. Решение может быть как вещественным, так и комплексным числом.
Таблица ниже демонстрирует значения переменной в неполном квадратном уравнении в зависимости от значений коэффициентов:
| Значение a | Значение b | Значение c | Значение переменной |
|---|---|---|---|
| Ненулевое | Ненулевое | Ненулевое | Зависит от решения уравнения |
| Нулевое | Ненулевое | Ненулевое | Зависит от решения линейного уравнения |
| Ненулевое | Нулевое | Ненулевое | Зависит от решения квадратного уравнения |
| Ненулевое | Ненулевое | Нулевое | Зависит от решения уравнения без свободного члена |
Способы определения значения переменной

Дискриминант – это число, которое позволяет определить, какое количество решений имеет уравнение. Если дискриминант больше нуля, то уравнение имеет два различных корня. Если дискриминант равен нулю, то уравнение имеет один корень, а если дискриминант меньше нуля, то уравнение не имеет решений.
Для определения значения переменной нужно:
- Вычислить дискриминант по формуле: D = b^2 - 4ac, где a, b, и c – это коэффициенты уравнения.
- Проверить значение дискриминанта:
- Если D > 0, то уравнение имеет два решения, значения которых можно найти по формулам: x1 = (-b + √D) / (2a) и x2 = (-b - √D) / (2a).
- Если D = 0, то уравнение имеет одно решение, которое можно найти по формуле: x = -b / (2a).
- Если D
Также можно использовать другие методы для определения значения переменной в неполном квадратном уравнении, такие как метод графического представления, метод подстановки, метод выделения полного квадрата и др. Каждый из этих методов подходит для разных типов уравнений и может использоваться в зависимости от поставленной задачи.
| Метод | Описание |
|---|---|
| Метод дискриминанта | Позволяет вычислить дискриминант и определить количество решений уравнения. |
| Метод графического представления | Основывается на построении графика функции и определении точки пересечения с осью абсцисс. |
| Метод подстановки | Позволяет вместо переменной подставить найденное значение и проверить его. |
| Метод выделения полного квадрата | Основывается на преобразовании уравнения к виду (а - b)^2 = 0 и нахождении значения переменной. |
Выбор метода определения значения переменной зависит от сложности уравнения, доступных данных и требуемой точности решения. Важно учитывать, что неполное квадратное уравнение может иметь разные варианты решений, и выбор метода может существенно влиять на результат.
Особенности решения неполного квадратного уравнения

Решение неполного квадратного уравнения производится путем применения формулы дискриминанта: D = b^2 - 4ac. Дискриминант позволяет определить количество корней и их характер при решении квадратного уравнения.
| Дискриминант (D) | Тип решения |
|---|---|
| D > 0 | Уравнение имеет два различных корня. |
| D = 0 | Уравнение имеет один корень (корни совпадают). |
| D | Уравнение не имеет действительных корней (корни комплексные). |
Если дискриминант положителен (D > 0), то значение переменной можно найти с помощью формулы: x = (-b ± √D) / 2a. Здесь знак "±" указывает на два возможных значения переменной.
Если дискриминант равен нулю (D = 0), то значение переменной находится при помощи формулы: x = -b / 2a. Здесь уравнение имеет один корень.
Если дискриминант отрицательный (D
Зависимость значения переменной от коэффициентов уравнения
Значение переменной в неполном квадратном уравнении вида ax^2 + bx = 0 зависит от коэффициентов a и b. Для определения значения переменной необходимо решить уравнение и выразить x.
Если коэффициент a равен нулю (a = 0), то уравнение принимает вид bx = 0. В этом случае, если коэффициент b также равен нулю (b = 0), то любое значение x является решением уравнения. Если же b не равно нулю (b ≠ 0), то решением уравнения будет x = 0.
Если коэффициент a не равен нулю (a ≠ 0), то уравнение будет иметь одно или два решения, в зависимости от значений коэффициентов a и b. Решение уравнения можно получить с помощью дискриминанта.
Если дискриминант D = b^2 - 4ac положителен (D > 0), то уравнение имеет два различных корня. В этом случае значения переменной x вычисляются с помощью формулы:
x1 = (-b + sqrt(D)) / (2a)
x2 = (-b - sqrt(D)) / (2a)
Если дискриминант D равен нулю (D = 0), то уравнение имеет один корень, и значение переменной x вычисляется по формуле:
x = -b / (2a)
Если дискриминант D отрицателен (D
Примеры решения неполного квадратного уравнения
- Пример 1: x^2 + 6x = 8 - 2x
Для начала, нужно привести уравнение к стандартному виду: x^2 + 6x + 2x - 8 = 0
Затем, раскрываем скобки и приводим подобные слагаемые: x^2 + 8x - 8 = 0
Далее, используем формулу дискриминанта для нахождения корней уравнения: D = b^2 - 4ac
В данном случае, коэффициенты равны: a = 1, b = 8, c = -8
Подставляем значения в формулу: D = 8^2 - 4 * 1 * -8 = 64 + 32 = 96
Так как дискриминант положительный, уравнение имеет два различных корня.
Далее, используем формулу для нахождения корней уравнения: x1,2 = (-b ± √D) / 2a
Подставляем значения в формулу: x1 = (-8 + √96) / 2 = (-8 + 4√6) / 2 = -4 + 2√6
Подставляем значения в формулу: x2 = (-8 - √96) / 2 = (-8 - 4√6) / 2 = -4 - 2√6
- Пример 2: 5x^2 - 3x = 2x -10
Приводим уравнение к стандартному виду: 5x^2 - 3x - 2x + 10 = 0
Сокращаем подобные слагаемые: 5x^2 - 5x + 10 = 0
Выносим общий множитель: 5(x^2 - x + 2) = 0
Приводим квадратный трехчлен в квадратное уравнение: (x - 1/2)^2 + 3/4 = 0
Так как сумма квадратов никогда не может быть отрицательной, у данного уравнения нет решений.
Благодаря этим примерам можно увидеть различные сценарии решений неполных квадратных уравнений, а также понять, что иногда уравнение может не иметь решений вовсе. Важно правильно приводить уравнение к стандартному виду и использовать формулы для нахождения дискриминанта и корней уравнения.



