Чему равно перемещение точки движущейся по окружности

Перемещение точки по окружности является одной из основных задач геометрии. Оно широко применяется в различных областях науки и техники, например, в физике, механике, астрономии и компьютерной графике. Понимание численного значения перемещения точки по окружности позволяет решать различные задачи, связанные с движением тел.

Для определения численного значения перемещения точки по окружности необходимо знать радиус окружности и угол, на который точка смещается относительно начального положения. Радиус окружности обозначается символом R, а угол – символом θ.

Применяя тригонометрические функции, можно вычислить смещение точки по оси x и оси y. Если точка начинает движение из начальной точки с координатами (x₀, y₀), то ее новое положение будет иметь координаты:

x = x₀ + R * cos(θ)

y = y₀ + R * sin(θ)

Таким образом, представляя угол в радианах, можно определить положение точки на окружности, вычислив значения x и y. Эти формулы играют важную роль при моделировании различных процессов и явлений, связанных с движением по окружности.

Понятие перемещения точки

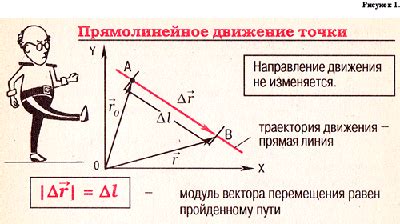
Перемещение точки на окружности обозначает изменение её положения при движении вдоль окружности. При перемещении точки на окружности она остается на окружности, но меняет свои координаты.

Перемещение точки на окружности может быть описано посредством двух параметров:

1. Угла поворота - это угол между начальным положением точки и её текущим положением на окружности.
2. Длины дуги - это расстояние, которое прошла точка на окружности от начального положения до текущего положения.

Угол поворота измеряется в градусах или радианах и показывает, насколько точка сместилась вдоль окружности.

Длина дуги измеряется в единицах длины и показывает, сколько длины окружности прошла точка от начального положения до текущего положения.

Изменение положения точки на окружности может использоваться для определения различных свойств окружности и для решения разнообразных задач в геометрии и физике.

Определение и значение перемещения точки по окружности

Перемещение точки по окружности может быть определено как изменение ее положения относительно начальной точки на окружности. Перемещение точки по окружности может иметь как прямое, так и обратное направление, и представляет собой путь, который точка проходит от начального положения к конечному.

Значение перемещения точки по окружности зависит от длины дуги, которую точка проходит от начального положения к конечному. Длина дуги выражается в радианах или градусах, и определяется углом, на который смещается точка относительно начального положения.

Перемещение точки по окружности является важным понятием в геометрии и других науках. Оно используется для определения позиции объектов, траектории движения и расчета различных параметров окружности, таких как радиус, длина дуги и площадь.

Параметры, определяющие перемещение точки

Перемещение точки по окружности зависит от нескольких важных параметров:

• Радиус окружности - это расстояние от центра окружности до точки, которая перемещается по ней. Радиус определяет размер окружности и влияет на протяженность перемещения точки.
• Начальный угол - это угол между осью OX и линией, соединяющей центр окружности с начальным положением точки. Он задает начальную ориентацию точки на окружности.
• Скорость - это параметр, определяющий, как быстро точка перемещается по окружности. Скорость может быть постоянной или изменяться в течение движения.
• Время - время, прошедшее с начала движения точки. Оно используется для вычисления текущего положения точки на окружности.

Изменение этих параметров позволяет контролировать всевозможные движения точки по окружности, такие как вращение вокруг центра, вращение вокруг другой точки, движение по спирали и так далее.

Расчет численного значения перемещения точки

Для расчета численного значения перемещения точки по окружности необходимо учесть ее радиус и угол поворота.

Чтобы получить значение перемещения точки, необходимо использовать формулу:

Следует отметить, что угол поворота должен быть в радианах. Если угол задан в градусах, его необходимо перевести в радианы, умножив на коэффициент перевода равный π/180.

Таким образом, численное значение перемещения точки расчитывается по следующей формуле:

Используя данную формулу, можно вычислить точное или приближенное значение перемещения точки по окружности. Это может быть полезно, например, при моделировании движения объектов в компьютерных программных средах или в решении задач на физическую активность.

Применение численного значения перемещения точки

При изучении движения точки по окружности важно иметь возможность рассчитать ее перемещение на каждом шаге. Для этого можно использовать численные методы, которые позволяют оценить приближенное значение координат точки на окружности.

Одним из таких методов является метод Эйлера. Он основан на разбиении времени на малые интервалы и последовательном расчете значений координат точки на каждом шаге. Этот метод имеет простую формулу и хорошую точность при достаточно малом шаге. Однако, при увеличении шага ошибка становится больше.

Другим распространенным методом является метод Рунге-Кутты. Он использует несколько промежуточных точек для более точного вычисления значения координаты. Этот метод позволяет получить более точное значение перемещения точки на каждом шаге, но требует более сложных вычислений и больше вычислительных ресурсов.

Численное значение перемещения точки по окружности на практике часто применяется в различных областях, таких как физика, инженерия, компьютерная графика и другие. Оно позволяет моделировать и анализировать движение объектов, в том числе и точек на окружности, с высокой точностью и контролем.