Чему равна площадь трапеции через среднюю линию и как ее вычислить?

Трапеция - это геометрическая фигура, которая имеет две параллельные стороны и две непараллельные стороны, которые называются основаниями. Средняя линия трапеции - это отрезок, соединяющий середины двух непараллельных сторон.

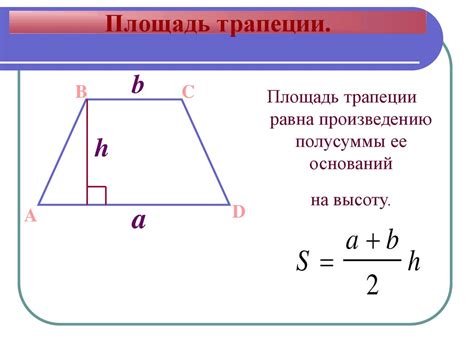
Площадь трапеции можно выразить через её основания и среднюю линию. Формула для расчёта площади трапеции звучит следующим образом:

S = (a + b) * h / 2,

где S - площадь трапеции, a и b - длины оснований трапеции, h - высота трапеции (расстояние между основаниями).

Таким образом, для нахождения площади трапеции через среднюю линию необходимо знать длины её оснований и длину средней линии. Подставляя эти значения в формулу, мы можем получить точный результат.

Определение понятия "Трапеция"

Основные элементы трапеции:

• Боковые стороны: это две непараллельные стороны трапеции.
• Основания: это параллельные стороны трапеции. Основания могут быть разной длины.
• Высота: это отрезок, проведенный перпендикулярно между основаниями и соединяющий их. Высота может быть произвольной длины и может находиться как внутри трапеции, так и за ее пределами.
• Средняя линия: это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия параллельна основаниям и равна полусумме длин оснований.

Трапеция может быть равнобедренной, если ее боковые стороны равны, или разносторонней, если боковые стороны не равны.

Средняя линия трапеции: определение и свойства

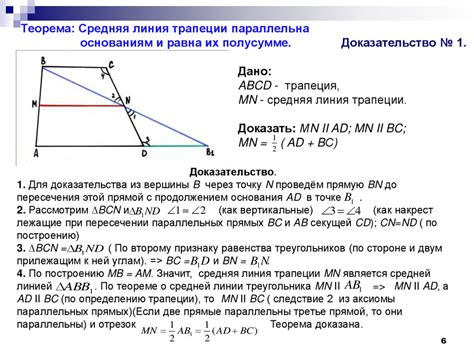
Свойства средней линии трапеции:

1. Средняя линия трапеции параллельна основаниям и равна полусумме их длин: м = (а + b) / 2, где а и b - длины оснований.
2. Средняя линия трапеции равна полусумме диагоналей: м = (d₁ + d₂) / 2, где d₁ и d₂ - диагонали трапеции.
3. Средняя линия трапеции делит фигуру на две равные площади.
4. Сумма длин оснований трапеции равна удвоенной длине средней линии: а + b = 2м.

Зная длину средней линии трапеции, можно рассчитать площадь данной фигуры, используя формулу: S = м * н, где н - высота трапеции.

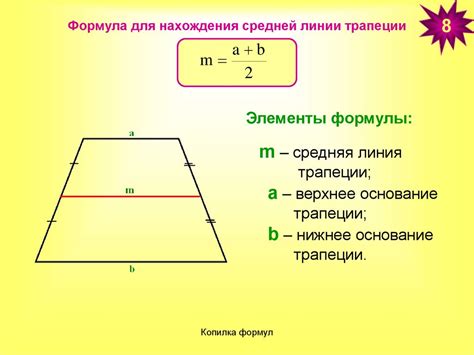
Формула для вычисления средней линии трапеции

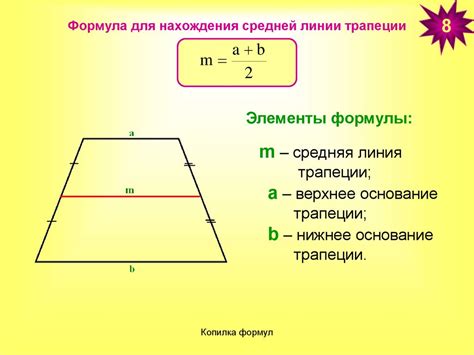
средняя_линия = (основание_1 + основание_2) / 2

Где:

• средняя_линия - длина средней линии трапеции;
• основание_1 - длина первого основания трапеции;
• основание_2 - длина второго основания трапеции.

Чтобы вычислить площадь трапеции через среднюю линию, достаточно умножить ее длину на высоту трапеции и разделить полученное значение на 2:

площадь = (средняя_линия * высота) / 2

Где:

• площадь - площадь трапеции;
• высота - высота трапеции.

Используя формулу для вычисления средней линии трапеции, можно легко оценить площадь этой геометрической фигуры.

Формула средней линии трапеции через ребра

Где:

• a и b - длины параллельных сторон трапеции
• h - высота трапеции, перпендикулярная параллельным сторонам

Таким образом, площадь трапеции через среднюю линию можно найти, зная длины ее параллельных сторон и высоту. А длину средней линии можно вычислить, используя длины ребер трапеции.

Формула средней линии трапеции через площадь

Средняя линия трапеции - это отрезок, соединяющий середины ее параллельных сторон. В отличие от боковых сторон, средняя линия необходима для нахождения некоторых других параметров трапеции, таких как длины диагоналей и радиусов вписанной и описанной окружностей.

Формула для нахождения средней линии трапеции через ее площадь выглядит следующим образом:

Средняя линия = 2 * (площадь трапеции) / (сумма оснований)

Для применения этой формулы необходимо знать площадь трапеции и сумму ее оснований. Зная эти величины, можно легко найти среднюю линию трапеции.

Например, пусть у нас есть трапеция с площадью 50 квадратных единиц и суммой оснований 10 единиц. Подставляя эти значения в формулу, мы получаем:

Средняя линия = 2 * 50 / 10 = 10

Таким образом, в данном случае средняя линия трапеции равна 10 единицам.

Используя данную формулу, можно легко находить среднюю линию трапеции по известным параметрам, что значительно упрощает решение геометрических задач, связанных с этой фигурой.

Связь между средней линией и площадью трапеции

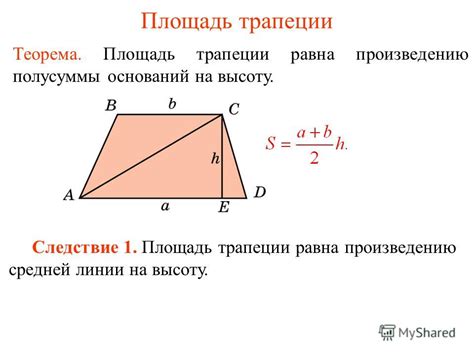
Средняя линия трапеции - это отрезок, соединяющий середины боковых сторон.

Существует простая формула, позволяющая вычислить площадь трапеции через среднюю линию:

1. Найдите длину средней линии трапеции, используя известные значения или геометрические выкладки.
2. Запишите формулу для вычисления площади трапеции: Площадь = (длина средней линии × высота) / 2.
3. Подставьте значения длины средней линии и высоты в формулу и произведите вычисления.

Определение площади трапеции через среднюю линию позволяет более просто и удобно решать задачи, связанные с нахождением площади этой геометрической фигуры.

Как вычислить площадь трапеции через среднюю линию

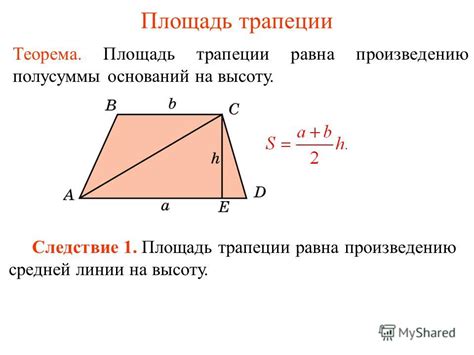
Средняя линия - это отрезок, соединяющий середины параллельных сторон трапеции. Она является геометрическим средним двух оснований трапеции.

Для вычисления площади трапеции через среднюю линию используется следующая формула:

S = h * m

где:

• S - площадь трапеции
• h - высота трапеции
• m - длина средней линии

Чтобы вычислить площадь трапеции через среднюю линию, необходимо знать высоту и длину средней линии. Высоту можно измерить перпендикулярно к основаниям, а длину средней линии можно определить как полусумму длин оснований.

Например, если основание трапеции равно 5 см, а средняя линия равна 8 см, то площадь трапеции будет:

S = h * m = 5 см * 8 см = 40 см²

Таким образом, площадь трапеции через среднюю линию составляет 40 см².

Практические примеры вычисления площади трапеции через среднюю линию

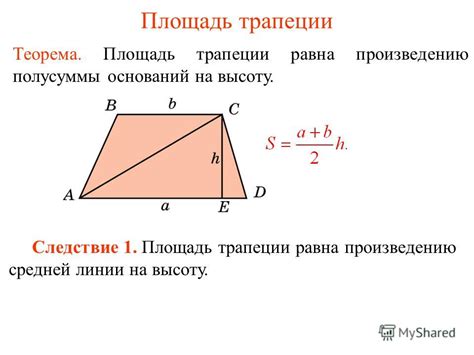
Площадь трапеции может быть вычислена с использованием формулы, которая использует длину средней линии. Рассмотрим несколько примеров применения этой формулы на практике.

Пример 1:

Допустим, у нас есть трапеция с основаниями длиной 5 см и 9 см, а длина средней линии составляет 6 см. Чтобы вычислить площадь этой трапеции, мы можем использовать следующую формулу:

S = (a + b) * h / 2

где a и b - длины оснований трапеции, а h - длина средней линии.

Подставим значения в формулу:

S = (5 + 9) * 6 / 2

S = 14 * 6 / 2

S = 84 / 2

S = 42

Ответ: площадь этой трапеции равна 42 квадратным сантиметрам.

Пример 2:

Рассмотрим другую трапецию с основаниями длиной 6 см и 10 см, а длина средней линии равна 8 см.

Используя формулу для вычисления площади трапеции через среднюю линию, мы получим:

S = (6 + 10) * 8 / 2

S = 16 * 8 / 2

S = 128 / 2

S = 64

Ответ: площадь этой трапеции равна 64 квадратным сантиметрам.

Это были примеры практического применения формулы для вычисления площади трапеции через среднюю линию. Надеюсь, данная информация поможет вам легко и точно рассчитать площадь трапеции в своих задачах и проектах.