Дуга - это часть окружности, которая образуется между двумя точками на окружности. Дуга может быть определена различными способами, включая длину, радиус и центральный угол.
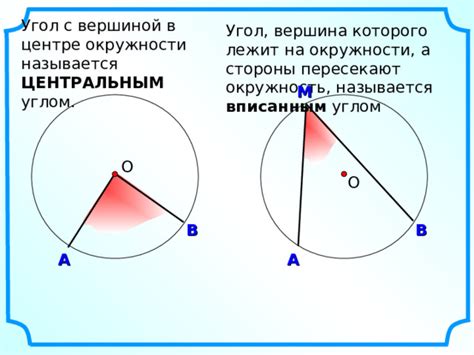
Центральный угол - это угол, образованный двумя лучами, исходящими из центра окружности и проходящими через две точки на окружности. Он может быть измерен в градусах или радианах и является основой для определения дуги, опирающейся на этот угол.
Теперь, когда мы знаем, что такое дуга и центральный угол, можно понять, чему равна дуга, опирающаяся на центральный угол. Длина дуги зависит от радиуса окружности и измеренного угла. Существует формула для вычисления длины дуги: длина дуги равна произведению угла в радианах и радиуса окружности.
Применение этой формулы может быть полезно при решении различных задач, связанных с окружностями и геометрией. Например, можно использовать эту формулу для вычисления длины дуги, зная радиус окружности и значение центрального угла.
Что такое дуга?

Дуга также может опираться на центральный угол, который измеряет угол между радиусами, соединяющими центр окружности с концами дуги. Дуга, опирающаяся на угол в 90 градусов, называется четвертью окружности, а дуга, опирающаяся на угол в 180 градусов, называется полуокружностью.
Дуги часто используются в геометрии и тригонометрии для измерения углов, вычисления длины дуги и решения различных задач связанных с окружностями. Они также находят применение в строительстве, навигации, архитектуре и других областях науки и техники.
Основные понятия
При изучении дуг, опирающихся на центральный угол, необходимо понимать ряд основных понятий:
| Угол | – геометрическая фигура, образованная двумя лучами, которые имеют общее начало, называемое вершиной угла. |
| Центральный угол | – угол, вершина которого совпадает с центром окружности, а стороны лежат на дуге этой окружности. |
| Дуга | – криволинейный сегмент окружности, определяемый двумя точками на окружности. |
| Длина дуги | – расстояние по окружности между двумя точками, определяющими дугу. |
Знание этих понятий позволяет корректно решать задачи, связанные с расчетом и изучением дуг, опирающихся на центральный угол.
Геометрическое определение

Дуга, опирающаяся на центральный угол, представляет собой часть окружности, ограниченную двумя радиусами и углом между ними. Эта дуга обладает следующими свойствами:
- Если центральный угол меньше 180 градусов, то дуга называется острым или меньшим секущим;
- Если центральный угол равен 180 градусов, то дуга называется прямым или семикилометровым;
- Если центральный угол больше 180 градусов, то дуга называется тупым или большим секущим;
- Зная радиус окружности и центральный угол, можно вычислить длину дуги с помощью формулы: длина дуги = (центральный угол / 360) * (2 * π * радиус).
Дуги, опирающиеся на центральные углы, широко применяются в геометрии и тригонометрии, а также в задачах, связанных с изучением окружностей и кругов. Это важное геометрическое понятие помогает различным наукам и практическим областям при работе с измерениями, построениями и расчетами.
Значение для изучения окружности
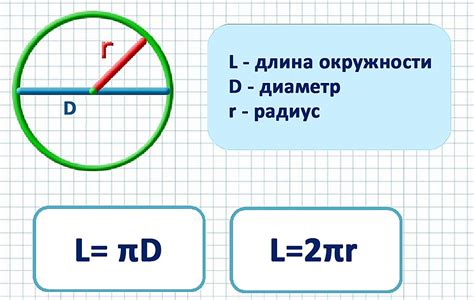
Дуга, опирающаяся на центральный угол, является одним из важных понятий, связанных с окружностями. Центральный угол – это угол, вершина которого совпадает с центром окружности, а стороны представлены лучами, исходящими из центра и заканчивающимися на окружности.
Дуга, опирающаяся на центральный угол, - это часть окружности, ограниченная двумя точками, которые также образуют центральный угол. Дуга может быть частью пути окружности между двумя точками или полной окружностью.
Изучение дуг, опирающихся на центральные углы, помогает понять различные свойства окружностей и применять их в решении задач и проблем. Это понимание позволяет рассматривать окружности с различных точек зрения и использовать их в различных областях, таких как физика, инженерия, геометрия и другие.
Как определить длину дуги
Формула для определения длины дуги выглядит следующим образом:
L = r * θ
где L - длина дуги, r - радиус окружности, θ - центральный угол, выраженный в радианах.
Чтобы определить длину дуги, необходимо знать радиус окружности и центральный угол в радианах. Если центральный угол выражен в градусах, его необходимо преобразовать в радианы, используя соотношение: θ (рад) = (π * θ (град)) / 180.
После того как вы найдете значение центрального угла в радианах, умножьте его на радиус окружности, чтобы получить длину дуги.
Зная эту формулу и умея преобразовывать углы из градусов в радианы, вы сможете легко определить длину дуги на окружности. Это пригодится в различных сферах деятельности и поможет вам лучше понять геометрические законы мира.
Формула для вычисления длины дуги
Длина дуги = (мера угла в радианах) × (радиус окружности)
Для вычисления длины дуги, нам понадобится знать меру центрального угла в радианах и радиус окружности.
Например, если центральный угол равен 45°, а радиус окружности равен 5 единиц, то формула будет выглядеть следующим образом:
Длина дуги = (45° × π/180) × 5 = (π/4) × 5 ≈ 3.93
Таким образом, длина дуги в данном случае составляет примерно 3.93 единиц.
Связь с центральным углом
Дуга, связанная с центральным углом, представляет собой часть окружности между точками начала и конца дуги. Она является дугой, которая соединяет две точки, принадлежащие окружности, и опирающиеся на центральный угол.
Величина дуги, опирающейся на центральный угол, напрямую связана с величиной самого угла. Если два центральных угла равны, то дуги, которые ими опираются, также будут равны. Также величина дуги будет зависеть от радиуса окружности - чем больше радиус, тем длиннее дуга.
Связь с центральным углом позволяет нам определить величину дуги и наоборот - зная величину дуги, можно определить центральный угол, опирающийся на эту дугу.
Как найти дугу, опирающуюся на центральный угол
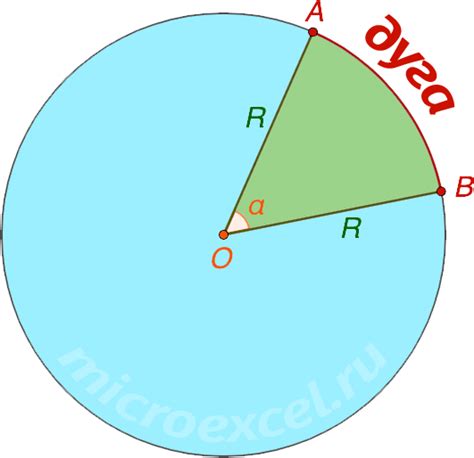
Если вам известен центральный угол и радиус окружности, вы можете легко найти длину дуги, опирающейся на этот угол.
Для начала вам необходимо знать, что центральный угол измеряется в градусах. Давайте обозначим центральный угол как "α".
Чтобы найти длину дуги, вы можете воспользоваться следующей формулой:
Длина дуги = (α/360) * 2π * r
Где:
- α - центральный угол (в градусах)
- π - число пи, примерно равное 3.14159
- r - радиус окружности
После подстановки значений в формулу, вы получите длину дуги в единицах измерения радиуса.
Если вместо градусов центральный угол задан в радианах, формула будет следующей:
Длина дуги = α * r
Обратите внимание, что результат будет выражен в радианах. Если вам необходимо получить длину дуги в других единицах измерения, вам придется преобразовать ее.
Значение дуги в геометрических построениях

Дуга, опирающаяся на центральный угол, имеет особое значение. Центральный угол - это угол, вершина которого находится в центре окружности, а сторонки угла проходят через точки, определяющие дугу. Значение дуги в геометрических построениях зависит от значения центрального угла, опирающегося на эту дугу.
Если центральный угол равен 360 градусов (или 2π радиан), то дуга, опирающаяся на него, будет равна длине всей окружности. Это значение дуги называется полной окружностью.
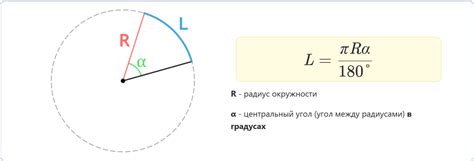
Если центральный угол меньше 360 градусов (или 2π радиан), то дуга, опирающаяся на него, будет меньше длины всей окружности и зависит от величины этого угла. Можно использовать формулу для расчета длины дуги:
L = (θ/360) * 2π * r
где L - длина дуги, θ - величина центрального угла в градусах, r - радиус окружности.
Таким образом, значение дуги в геометрических построениях зависит от значения центрального угла, опирающегося на эту дугу. Понимание этого позволяет производить точные измерения и строить точные геометрические фигуры. Дуги также широко используются в архитектуре, инженерии и других областях, где точные геометрические построения являются необходимыми.
Примеры использования дуги
Дуга, опирающаяся на центральный угол, используется в различных областях, включая математику, геометрию и физику. Вот несколько примеров использования этого понятия:
| Пример | Описание |
|---|---|
| Построение окружности | Дуга, опирающаяся на центральный угол, играет ключевую роль в построении окружности. Для построения окружности нужно определить центр и радиус, а затем построить дугу с углом в 360 градусов, чтобы получить полную окружность. |
| Измерение углов | Дуга, опирающаяся на центральный угол, используется для измерения углов в градусах. Угол с противолежащей дугой в 180 градусов называется прямым углом, а угол с противолежащей дугой в 90 градусов - прямым углом. |
| Арка в архитектуре | Дуги, опирающиеся на центральные углы, часто используются в архитектуре для создания арок. Арка - это кривая форма, состоящая из дуги, опирающейся на центральный угол, и двух стоек. Арки могут сделать здание более привлекательным и эстетически приятным. |
Это только некоторые примеры использования дуги, опирающейся на центральный угол. Это понятие имеет широкий спектр применений и может быть полезным в различных областях знаний и искусств.



