Окружность - это фигура, которая представляет собой замкнутую кривую линию, состоящую из точек, удаленных от одной точки, называемой центром, на одинаковое расстояние. Длина окружности - это расстояние между точками на окружности.
Если известен радиус окружности, то длину окружности можно вычислить с помощью формулы: длина окружности равна произведению числа π (пи) на удвоенный радиус или L = 2πr. Число π является одной из наиболее загадочных и интересных констант в математике и имеет приближенное значение 3,14.
Если же мы говорим о полуокружности, то ее длина будет равна половине длины полной окружности или L = πr. Полуокружность является половиной окружности и обладает своими уникальными свойствами.
Длина числовой окружности: формула и примеры вычисления
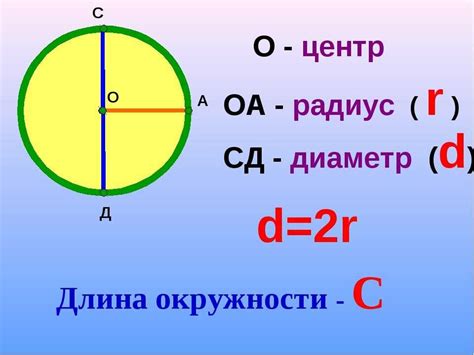
Формула для вычисления длины числовой окружности следующая:
C = 2πr
Где C - длина окружности, π - математическая константа (приближенно равная 3.14159), r - радиус окружности.
Пример вычисления длины числовой окружности:
- При заданном радиусе окружности r = 5
- C = 2πr = 2 * 3.14159 * 5 = 31.4159
Таким образом, длина числовой окружности с радиусом 5 равна 31.4159.
Зная формулу для вычисления длины числовой окружности, можно решать множество задач как в школьной, так и в высшей математике.
Понятие длины окружности
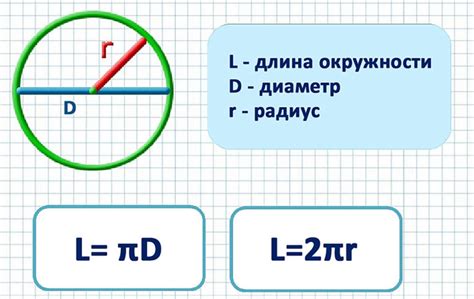
Таким образом, длина окружности равна удвоенному значению числа π, умноженному на радиус. Эта формула позволяет определить длину окружности, зная ее радиус или диаметр.
Для вычисления длины окружности также можно использовать таблицу значений. Ниже приведена таблица, в которой указаны некоторые значения длины окружности для разных радиусов:
| Радиус | Длина окружности |
|---|---|
| 1 | 6,28 |
| 2 | 12,57 |
| 3 | 18,85 |
| 4 | 25,13 |
| 5 | 31,42 |
Таким образом, зная радиус окружности, мы можем легко вычислить ее длину и использовать данную информацию, например, для планирования строительства или расчета необходимого материала.
Как вычислить длину числовой окружности
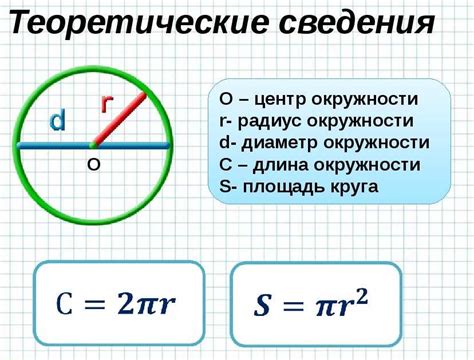
Для того чтобы вычислить длину числовой окружности, необходимо знать значение радиуса. Если радиус неизвестен, его можно найти, зная диаметр окружности и применив следующую формулу: r = d/2, где r – радиус, а d – диаметр окружности.
Пример вычисления длины числовой окружности:
| Радиус (r) | Длина окружности (C) |
|---|---|
| 1 | 2π |
| 2 | 4π |
| 3 | 6π |
Таким образом, длина числовой окружности будет увеличиваться пропорционально радиусу окружности.
Зная значение радиуса, можно легко вычислить длину числовой окружности по указанной формуле. Полученное значение может быть полезным при решении геометрических задач или в других областях, связанных с окружностями.
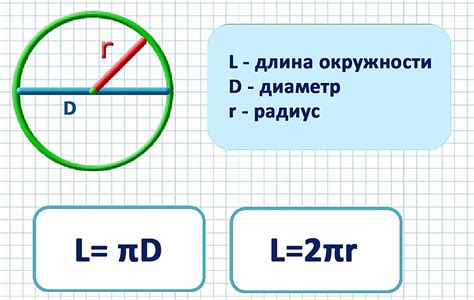
Формула для вычисления длины окружности
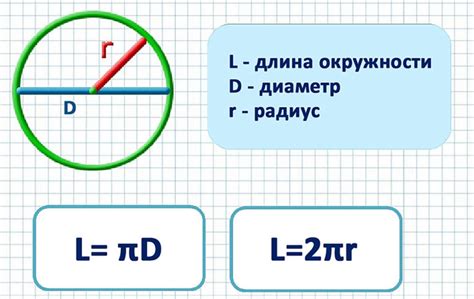
L = 2 * π * R,
где L - длина окружности, π - математическая константа, примерное значение которой равно 3.14, а R - радиус окружности.
Таким образом, чтобы вычислить длину окружности, необходимо умножить радиус на число 2 и на математическую константу π. Эта формула позволяет нам точно определить длину числовой окружности или полуокружности.
Примеры вычисления длины числовой окружности

Длина числовой окружности может быть вычислена с использованием формулы длины окружности:
Длина окружности = 2π * радиус
Для примера, рассмотрим окружность с радиусом 5:
Длина окружности = 2π * 5 = 10π
Таким образом, для окружности с радиусом 5, длина числовой окружности равна 10π.
Другой пример - окружность с радиусом 3:
Длина окружности = 2π * 3 = 6π
Значит, для окружности с радиусом 3, длина числовой окружности равна 6π.
Точное значение длины числовой окружности зависит от значения числа π, которое является иррациональным числом. В большинстве случаев, значение π приближенно равно 3,14, поэтому возможно округление значений длины окружности.
Также стоит отметить, что длина числовой окружности выражается в единицах длины, которые соответствуют радиусу окружности.
Влияние радиуса на длину числовой окружности
Длина числовой окружности зависит от радиуса. Радиус числовой окружности представляет собой расстояние от центра окружности до ее периметра. Величина радиуса напрямую влияет на длину числовой окружности.
Формула для расчета длины числовой окружности: Длина = 2πr, где π (пи) представляет собой математическую константу, близкую к 3.14159, а r - радиус окружности.
Чем больше радиус числовой окружности, тем больше будет ее длина. Это связано с тем, что при увеличении радиуса увеличивается и периметр окружности. Когда радиус удваивается, длина окружности тоже удваивается.
Например, если радиус числовой окружности равен 5 единицам, то длина окружности будет равна примерно 31.42 единицам. Однако, при увеличении радиуса до 10 единиц, длина окружности увеличится до примерно 62.83 единицы.
Из этого следует, что радиус числовой окружности является определяющим фактором для ее длины. Чем больше радиус, тем больше длина окружности, а при уменьшении радиуса длина окружности также уменьшится.
Отношение длины полуокружности к длине окружности

Полуокружность - это половина окружности. Она образуется при отсечении окружности на две равные части. Длина полуокружности обозначается буквой L.
Чтобы найти отношение длины полуокружности к длине окружности, нужно разделить длину полуокружности на длину окружности.
Формула для вычисления длины окружности: C = 2 * π * r, где π - это число Пи (приближенно равное 3,14), а r - радиус окружности.
Формула для вычисления длины полуокружности: L = π * r.
Теперь можем найти отношение длины полуокружности к длине окружности: L/C = (π * r) / (2 * π * r) = 0,5.
Получается, что отношение длины полуокружности к длине окружности равно 0,5 или 1/2.
Использование длины окружности в геометрических задачах
Пример 1: Найдем площадь круга, зная его длину окружности. Для этого воспользуемся формулой S = (C^2) / (4π), где S - площадь круга, C - длина окружности, π - математическая константа, приближенное значение которой равно 3,14. Подставляем известные значения и получаем площадь.
Пример 2: Необходимо построить правильный шестиугольник радиусом R, зная длину его окружности. Периметр шестиугольника равен 6R, а значит, длина его стороны равна R. Длина стороны шестиугольника также равна длине окружности, поэтому полученное значение можно использовать для построения фигуры.
Пример 3: Рассмотрим задачу о поиске длины дуги окружности, если известен ее центральный угол и радиус. Для решения этой задачи используется пропорция между длиной окружности и углом в радианах: C = 2πR * (α / 360), где C - длина дуги, R - радиус, α - центральный угол. Подставляем известные значения и находим длину дуги окружности.
Таким образом, длина окружности является важным параметром в геометрических задачах и позволяет находить другие характеристики фигур. Зная этот параметр, можно решать задачи связанные с площадью, периметром, построением геометрических фигур и т.д.



