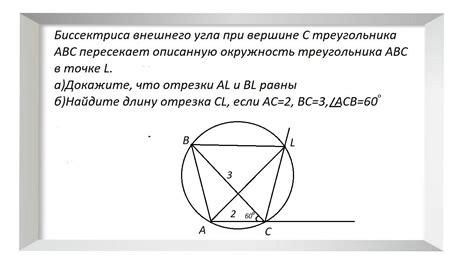
Равнобедренный треугольник – это треугольник, у которого две стороны равны по длине. Одно из свойств равнобедренного треугольника заключается в том, что его внешний угол, то есть угол, лежащий за пределами треугольника, равен сумме двух внутренних углов, не смежных с ним. Иными словами, внешний угол равнобедренного треугольника равен сумме внутреннего угла равнобедренного треугольника и угла, смежного с ним.
Для лучшего понимания, представим, что у нас есть равнобедренный треугольник ABC, где AB=BC. Пусть точка D находится за пределами треугольника ABC. Тогда угол D, внешний угол, будет равен сумме внутреннего угла В (угла при вершине B) и угла C (угла при вершине C). То есть мы можем записать следующее равенство: D = A + C.
Важно отметить, что внешний угол равнобедренного треугольника всегда больше любого из его внутренних углов, так как он представляет собой сумму двух углов. Знание этого свойства помогает в решении различных геометрических задач и вычислениях связанных с равнобедренными треугольниками.
Значение внешнего угла
Внешний угол в равнобедренном треугольнике равен разности двух внутренних углов. Так как в равнобедренном треугольнике два угла равны между собой, то для нахождения значения внешнего угла в равнобедренном треугольнике можно воспользоваться формулой:
Внешний угол = (180 - внутренний угол) / 2
Таким образом, значение внешнего угла в равнобедренном треугольнике можно вычислить, зная значение внутреннего угла. Это позволяет определить расположение внешнего угла по отношению к треугольнику и выпуклости его сторон.
Определение равнобедренного треугольника
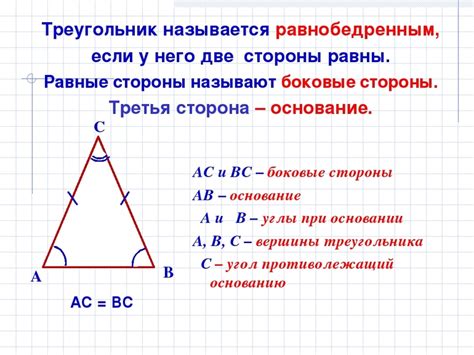
Таким образом, в равнобедренном треугольнике внешний угол, образованный продолжением одной из его боковых сторон с продолжением основания, всегда равен сумме двух равных внутренних углов, образованных при основании треугольника. Это свойство равнобедренных треугольников позволяет упростить решение различных задач, связанных с определением углов и сторон данной геометрической фигуры.
Что такое внешний угол
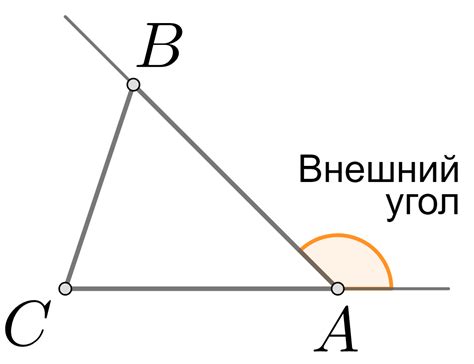
Рассмотрим равнобедренный треугольник ABC:
| Угол A | Угол B | Угол C | |
| Внутренний угол | α | β | γ |
| Внешний угол | 180°− α | 180°− β | 180°− γ |
Из таблицы видно, что внешние углы треугольника равнобедренного треугольника равны сумме двух внутренних углов, т.е.:
Внешний угол A = 180° - α
Внешний угол B = 180° - β
Внешний угол C = 180° - γ
Свойства внешнего угла
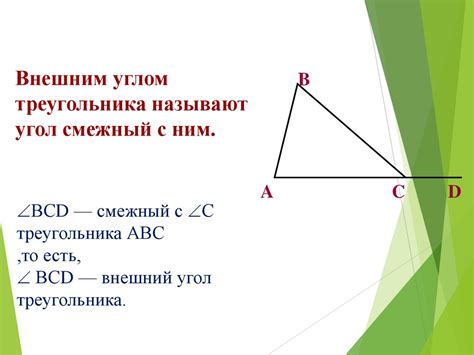
Внешний угол в равнобедренном треугольнике равен сумме двух внутренних углов, не смежных с данным внешним углом.
Если провести биссектрису внешнего угла, она будет являться продолжением одной из боковых сторон равнобедренного треугольника и будет делить внешний угол пополам.
Внешний угол также является смежным к вершинным углам равнобедренного треугольника. Вместе с этим вершинным углом и основанием, образует пару вертикальных углов.
| Свойства внешнего угла в равнобедренном треугольнике |
|---|
| Равен сумме двух внутренних углов |
| Делится пополам биссектрисой |
| Смежный к вершинным углам |
Формула расчета внешнего угла

Внешний угол в равнобедренном треугольнике может быть найден с использованием следующей формулы:
- Найдите значение каждого из двух равных углов внутри равнобедренного треугольника. Обозначим это значение как "a".
- Вычислите разность 180 градусов и значения "a". Полученное значение будет являться величиной внешнего угла равнобедренного треугольника.
Например, если значение каждого из двух равных углов внутри равнобедренного треугольника составляет 60 градусов, то значение внешнего угла будет равно 180 - 60 = 120 градусов.
Таким образом, формула расчета внешнего угла равнобедренного треугольника может быть представлена как:
Внешний угол = 180 - a
Примеры применения

Знание формулы для нахождения внешнего угла в равнобедренном треугольнике может быть полезным во многих ситуациях. Рассмотрим несколько примеров:
Архитектура Архитекторам важно знать внешние углы равнобедренных треугольников, чтобы правильно размещать элементы в проекте, такие как углы зданий, скаты крыш и окна. | Геодезия Геодезисты используют внешние углы равнобедренных треугольников для определения высот, длин и площадей объектов на местности. Это позволяет им делать точные измерения и создавать детальные карты. |
Изготовление мебели Мебельные производители часто сталкиваются с необходимостью создания равнобедренных треугольников при изготовлении столов, стульев и других предметов мебели. Знание внешнего угла помогает им создавать стабильные и прочные конструкции. | Топография Топографы используют внешние углы равнобедренных треугольников для изучения рельефа местности. Они могут измерять углы и расстояния между точками, чтобы построить подробные карты с высотными отметками и другой информацией. |
Внешний угол в равнобедренном треугольнике является важным концептом в различных областях, где требуется точная геометрия и измерения.



