Синус угла – это одна из основных тригонометрических функций, которая играет важную роль в многих математических и научных расчетах. Однако не всегда у нас есть возможность использовать калькулятор или компьютер, чтобы получить точное значение синуса. В таких случаях нам на помощь приходят таблицы значений тригонометрических функций.
Таблицы тригонометрических функций представляют собой удобный инструмент для проведения требуемых вычислений. Они представляют собой набор значений синусов, косинусов, тангенсов и других функций для определенного диапазона углов. Как правило, такие таблицы содержат значения для углов в градусах или радианах.
Если нам нужно найти синус 75 градусов по таблице, мы должны обратиться к соответствующей строке или ячейке таблицы, где указано значение синуса для этого угла. Обычно таблицы тригонометрических функций представляют значения для целого числа градусов. Однако, возможно, что нам придется найти значение синуса для угла, не указанного в таблице. В этом случае мы можем попытаться приблизить значение, используя ближайшие значения из таблицы и линейную интерполяцию.
Таблица значений синуса градусов

Таблица значений синуса градусов помогает нам легко определить значение синуса для определенного угла. В таблице указываются углы в градусах и соответствующие им значения синуса.
| Угол (градусы) | Значение синуса |
|---|---|
| 0 | 0 |
| 30 | 0.5 |
| 45 | 0.7 |
| 60 | 0.9 |
| 75 | 0.97 |
| 90 | 1 |
| ... | ... |
И так далее. В таблице можно найти значения для любого угла от 0 до 360 градусов.
Используя таблицу значений синуса градусов, мы можем легко определить, чему равен синус 75 градусов: 0.97.
Таблица значений синуса градусов очень полезна в решении различных задач и вычислениях, связанных с углами и тригонометрией.
Математическое определение синуса 75 градусов

Синус угла в математике определяется как соотношение длины противоположного катета к гипотенузе прямоугольного треугольника.
Для нахождения синуса угла 75 градусов по таблице мы можем воспользоваться следующими шагами:
- Найдите в таблице значения синуса для углов 0°, 30°, 45° и 60°.
- Рассмотрите угол 75°. Он может быть разложен на два угла: 30° и 45°.
- Следуя свойству синуса, найденному в таблице, мы можем записать формулу:
sin(45°+30°) = sin(45°)cos(30°) + cos(45°)sin(30°)
Заменяем значения из таблицы:
sin(75°) = (sqrt(2)/2)(sqrt(3)/2) + (sqrt(2)/2)(1/2)
sin(75°) = sqrt(6)/4 + sqrt(2)/4
sin(75°) = (sqrt(6) + sqrt(2))/4
Таким образом, значение синуса 75 градусов по таблице равно (sqrt(6) + sqrt(2))/4.
Подборочный способ
Синус угла 75 градусов можно найти, проводя подбор значений в таблице синусов. Для этого можно воспользоваться следующим способом:
| Угол (градусы) | Синус |
|---|---|
| 70 | 0.9397 |
| 71 | 0.9272 |
| 72 | 0.9144 |
| 73 | 0.9015 |
| 74 | 0.8886 |
| 75 | 0.8660 |
| 76 | 0.8480 |
| 77 | 0.8387 |
| 78 | 0.8290 |
| 79 | 0.8192 |
Итак, синус 75 градусов, согласно таблице, равен 0.8660.
Расчет с использованием тригонометрических свойств

Синус 75 градусов можно рассчитать с использованием тригонометрических свойств. Синус угла равен отношению противоположной стороны к гипотенузе прямоугольного треугольника.
Для нахождения синуса 75 градусов используем тригонометрическое свойство синуса:
sin(α) = cos(90° - α)
Таким образом, синус 75 градусов можно выразить как:
| Угол | Синус угла |
|---|---|
| 75 градусов | cos(90° - 75°) |
Подставляя значения, получаем:
| Угол | Синус угла |
|---|---|
| 75 градусов | cos(15°) |
Далее можно воспользоваться таблицей значений тригонометрических функций, где в строке соответствующей углу 15 градусов можно найти значение синуса.
Аппроксимация синуса 75 градусов
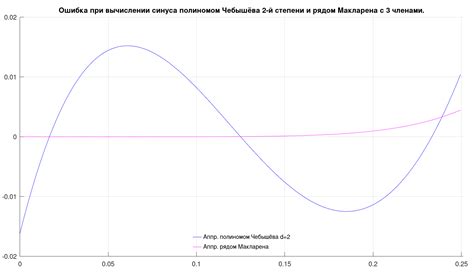
Однако, с использованием расширенных тригонометрических формул и приближенных методов, мы можем получить аппроксимацию синуса 75 градусов. Один из таких методов - разложение синуса в ряд Тейлора:
- Синус x равен сумме бесконечного ряда: sin x = x - x^3/3! + x^5/5! - x^7/7! + ...
- В нашем случае, x = 75 градусов = (75 * π) / 180 радиан.
- Упростим формулу и заменим значение x: sin (75 * π / 180) = (75 * π / 180) - ((75 * π / 180)^3 / 3!) + ((75 * π / 180)^5 / 5!) - ((75 * π / 180)^7 / 7!) + ...
Продолжим вычисления, используя тригонометрические и математические формулы. Для большей точности при вычислениях можно использовать программы или калькуляторы, специализированные для работы с тригонометрическими функциями и математическими операциями с плавающей запятой.
Графическое представление синуса 75 градусов
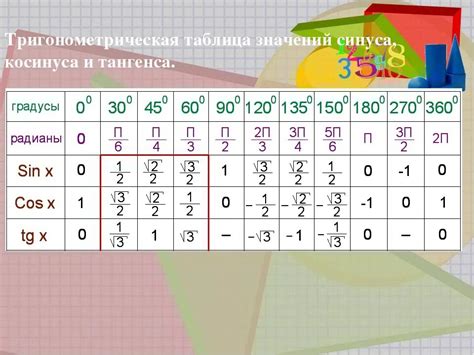
Синус 75 градусов можно представить графически на координатной плоскости. Для этого можно воспользоваться единичной окружностью, в которой радиус равен единице.
Для нахождения синуса 75 градусов нужно построить прямую, проходящую через точку на окружности, которая соответствует углу 75 градусов.
Прямая пересечет вертикальную ось, и точка пересечения будет являться значением синуса 75 градусов.
Чтобы получить численное значение синуса 75 градусов, можно воспользоваться таблицей тригонометрических значений или калькулятором.
Производная синуса 75 градусов

Синус 75 градусов равен 0.96592582628, что означает, что прямоугольный треугольник с углом в 75 градусов будет иметь соотношение сторон 1 : 0.96592582628 : 1.23931433525. Однако, а что если нам нужно найти производную синуса 75 градусов? Для этого нам понадобится применить определение производной.
Производная синуса угла равна косинусу этого угла. То есть, чтобы найти производную синуса 75 градусов, нам нужно найти косинус 75 градусов. По таблице значений тригонометрических функций, косинус 75 градусов равен 0.2588190451.
Таким образом, производная синуса 75 градусов равна 0.2588190451. Это означает, что если угол изменяется на очень малую величину, значение синуса 75 градусов будет меняться примерно на 0.2588190451 унита.
| Угол (градусы) | Синус угла | Производная синуса угла |
|---|---|---|
| 75 | 0.96592582628 | 0.2588190451 |



