В геометрии окружность - это фигура, которая представляет собой множество точек на плоскости, равноудаленных от определенной точки, называемой центром окружности. В окружности можно выделить два радиуса - вписанный и описанный. Радиус вписанной окружности является отрезком, соединяющим центр окружности с любой точкой на ее границе.
Радиус описанной окружности - это отрезок, соединяющий центр окружности с любой точкой, принадлежащей ее границе. В отличие от вписанной окружности, описанная окружность проходит через все вершины фигуры, на которой она построена. Таким образом, радиус описанной окружности всегда больше радиуса вписанной окружности.
Существует формула, которая позволяет вычислить радиус вписанной окружности по известным сторонам треугольника. Формула выглядит следующим образом: радиус вписанной окружности равен площади треугольника, деленной на полупериметр треугольника. Если известны радиусы вписанной и описанной окружностей, можно также вычислить площадь и периметр треугольника.
Доказательство равенства радиусов вписанной и описанной окружностей
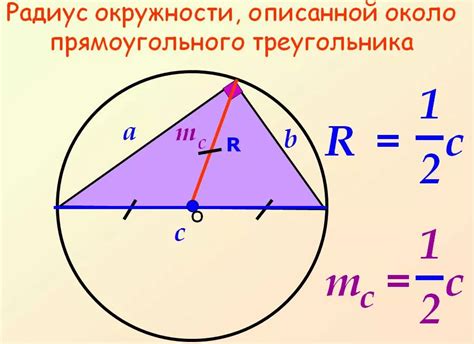
Для доказательства равенства радиусов вписанной и описанной окружностей используется свойство прямоугольного треугольника, описанного около исследуемого треугольника. Пусть имеется треугольник ABC с вписанной окружностью, касающейся сторон треугольника в точках D, E и F, а также описанной окружностью, проходящей через точки A, B и C.
Для начала рассмотрим вписанный треугольник AED. В этом треугольнике DE является средней линией, а значит, DE равно половине суммы сторон AD и AE. Также, по теореме о касательной и секущей, сегмент AD равен сегменту AF, так как они опираются на углы с одной и той же дугой.
Аналогичным образом, рассмотрим вписанный треугольник BDF. Так как BD равно половине суммы сторон AF и CF, а сторона AF равна стороне AD, то BD также равно половине суммы сторон AD и CF.
Определения основных понятий

Радиус описанной окружности - это отрезок, проведенный от центра описанной окружности до любой точки ее окружности.
Описание основных свойств вписанной и описанной окружности
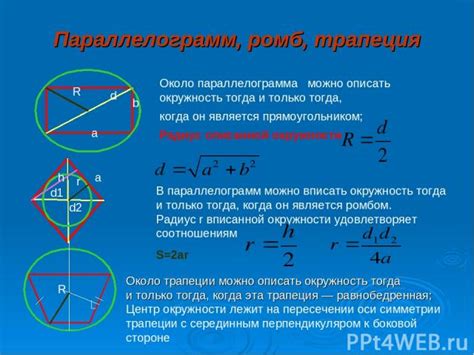
Вписанная окружность - это окружность, которая касается всех сторон треугольника. Ее центр лежит внутри треугольника, и радиус данной окружности обычно обозначается как r.
Описанная окружность - это окружность, которая проходит через вершины треугольника. Ее центр лежит на пересечении высот треугольника, и радиус данной окружности обычно обозначается как R.
Связь между радиусами вписанной и описанной окружности можно выразить следующим образом: радиус вписанной окружности (r) и радиус описанной окружности (R) взаимосвязаны с радиусом окружности, вокруг которой можно описать треугольник (r1), исходя из формулы r * R = r1^2.
Знание свойств вписанной и описанной окружности позволяет решать задачи, связанные с треугольниками, а также упрощает построение фигур и нахождение дополнительной информации о треугольнике.
Лемма о равенстве углов между касательной и хордой в окружности
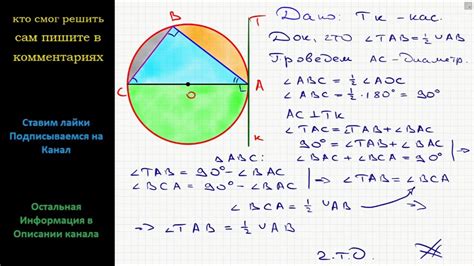
В этой лемме утверждается, что если из точки касания касательной к окружности провести хорду, то угол между касательной и хордой будет равен углу, опирающемуся на эту хорду и лежащему внутри окружности.
Доказательство этой леммы основывается на свойствах окружностей и угла внутри окружности:
- Внутри окружности угол, опирающийся на хорду, равен половине угла, опирающегося на дугу, содержащую эту хорду.
- Угол между касательной и хордой является углом между касательной и хордой, опирающейся на дугу, содержащую эту хорду.
- Пользуясь свойствами угла внутри окружности и свойствами касательной, можно утверждать, что углы между касательной и хордой равны.
Таким образом, лемма о равенстве углов между касательной и хордой в окружности является важным утверждением в геометрии и находит широкое применение при решении различных задач, связанных с окружностями и их свойствами.
Доказательство равенства радиусов

Для доказательства равенства радиусов вписанной и описанной окружностей рассмотрим произвольный треугольник ABC.
Пусть R1 и R2 - радиусы вписанной и описанной окружностей соответственно.
Известно, что вписанная окружность с центром в точке O касается сторон треугольника в точках D, E и F.
Также известно, что описанная окружность с центром в точке O' проходит через вершины треугольника и касается сторон треугольника только в одной точке.
Для доказательства равенства радиусов R1 и R2 рассмотрим отрезки AO и AO'.
Поскольку внутри треугольника существует только одна окружность, описанная вокруг него, и только одна окружность, вписанная в него, то точки O и O' совпадают.
Следовательно, радиусы R1 и R2 равны.
Треугольник ABC | Окружности |
Случай треугольника с прямым углом
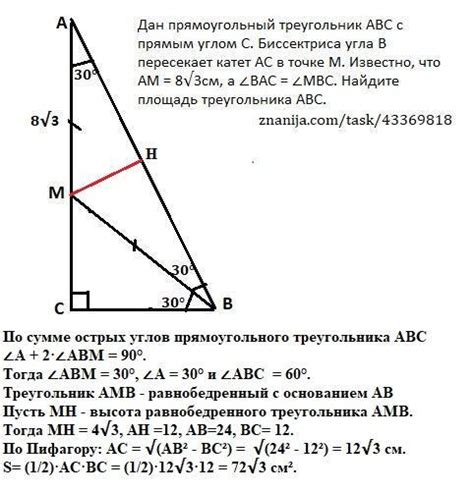
Пусть a, b и c - длины сторон треугольника, а R и r - радиусы описанной и вписанной окружностей соответственно.
Формулы для расчета радиусов:
| Описанная окружность | Вписанная окружность |
|---|---|
| R = c/2 | r = (a + b - c)/2 |
Таким образом, для треугольника с прямым углом известными сторонами, радиусы описанной и вписанной окружностей можно рассчитать по указанным формулам.
Итак, радиус вписанной окружности прямоугольного треугольника равен половине гипотенузы, или же равен произведению полупериметра треугольника и коэффициента, равного разности катетов, деленной на длину гипотенузы.
Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы.
Знание этих формул позволяет вычислять радиусы вписанной и описанной окружностей, что может быть полезным при решении различных задач геометрии и физики.





