Описанная окружность - это окружность, которая проходит через все вершины прямоугольника. То есть, каждая из четырех вершин лежит на окружности. Интересно, что радиус описанной окружности около прямоугольника имеет свое определенное значение, и его можно вычислить с помощью простой формулы.
Для того чтобы найти радиус описанной окружности, нам понадобится знание длин сторон прямоугольника. Пусть a - длина одной из сторон, а b - длина другой стороны. Тогда радиус описанной окружности вычисляется по формуле:
R = √((a/2)^2 + (b/2)^2)
Где R - радиус описанной окружности прямоугольника. Полученная формула позволяет нам находить радиус окружности, даже если у нас нет доступа к самому прямоугольнику, а есть только его стороны.
Интересно отметить, что радиус описанной окружности около прямоугольника всегда будет положительным числом. Это связано с тем, что значения длин сторон прямоугольника являются положительными числами, а в формуле радиуса присутствует извлечение квадратного корня. Также стоит отметить, что радиус описанной окружности около прямоугольника будет больше, чем половина диагонали прямоугольника.
Что такое радиус описанной окружности прямоугольника
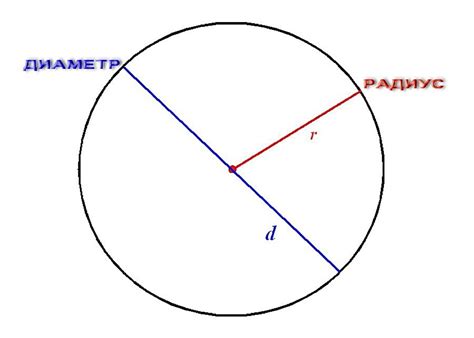
Диагональ прямоугольника - это отрезок, соединяющий противоположные вершины. Радиус описанной окружности является отрезком, проходящим через центр прямоугольника и соединяющим противоположные вершины. Отрезок радиуса описанной окружности делит диагональ прямоугольника пополам.
Радиус описанной окружности является важным параметром прямоугольника, так как он определяет размеры и геометрические свойства описанной окружности. Например, описанная окружность прямоугольника является наибольшей окружностью, которая может быть вписана в данный прямоугольник.
Для вычисления радиуса описанной окружности прямоугольника можно использовать формулу:
- Найдите длину диагонали прямоугольника с помощью теоремы Пифагора: диагональ^2 = ширина^2 + высота^2.
- Разделите длину диагонали на 2, чтобы получить радиус описанной окружности.
Теперь вы понимаете, что радиус описанной окружности прямоугольника - это важный математический параметр, который помогает определить размеры и свойства геометрической фигуры.
Радиус описанной окружности: определение и свойства
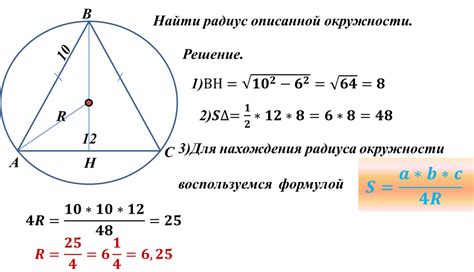
Радиус описанной окружности также обладает несколькими свойствами:
- Радиус описанной окружности является половиной длины диагонали прямоугольника. Если длина диагонали прямоугольника равна d, то радиус описанной окружности равен d/2.
- Радиус описанной окружности является наибольшей возможной длиной среди всех прямых отрезков, соединяющих угол прямоугольника с точками на его окружности.
- Радиус описанной окружности проходит через центр прямоугольника.
- Радиус описанной окружности равен половине длины хорды, если она проходит через центр окружности.
- Радиус описанной окружности является постоянной величиной для данного прямоугольника, независимо от его размеров или формы.
Использование радиуса описанной окружности позволяет определить геометрические свойства прямоугольника и использовать их в математических расчетах и приложениях.
Прямоугольник и его свойства
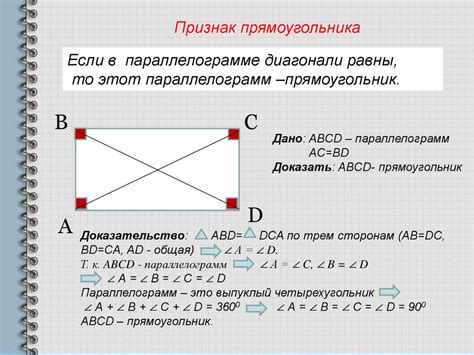
1. Углы: Прямоугольник имеет четыре прямых угла, каждый из которых равен 90 градусам. Это делает прямоугольник одним из самых узнаваемых геометрических фигур.
2. Стороны: Прямоугольник состоит из двух пар параллельных сторон. Каждая пара состоит из одной короткой и одной длинной стороны. Длина длинной стороны равна длине короткой стороны умноженной на два.
3. Диагонали: Прямоугольник имеет две диагонали, которые соединяют противоположные вершины. Длина каждой диагонали равна корню квадратному из суммы квадратов длины сторон.
4. Периметр: Периметр прямоугольника вычисляется как сумма длин всех его сторон.
5. Площадь: Площадь прямоугольника равна произведению длины его длинной стороны на длину короткой стороны.
Интересный факт: Радиус описанной окружности около прямоугольника, вычисляется по формуле: половина длины диагонали прямоугольника.
Как найти радиус описанной окружности по сторонам прямоугольника
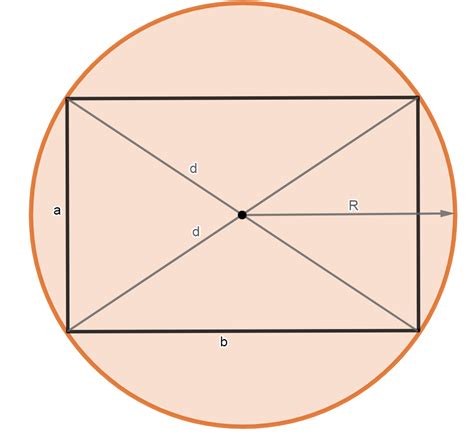
Радиус описанной окружности прямоугольника можно найти с помощью известных сторон прямоугольника.
Для этого нужно воспользоваться формулой: радиус описанной окружности равен половине диагонали прямоугольника.
Для нахождения длины диагонали прямоугольника можно воспользоваться теоремой Пифагора, зная длины его сторон.
Если стороны прямоугольника равны a и b, то длина его диагонали равна √(a^2 + b^2).
Полученное значение длины диагонали прямоугольника можно поделить на 2, чтобы найти радиус описанной окружности.
Таким образом, радиус описанной окружности прямоугольника равен √(a^2 + b^2) / 2, где a и b - длины сторон прямоугольника.
Теорема о радиусе описанной окружности для прямоугольника
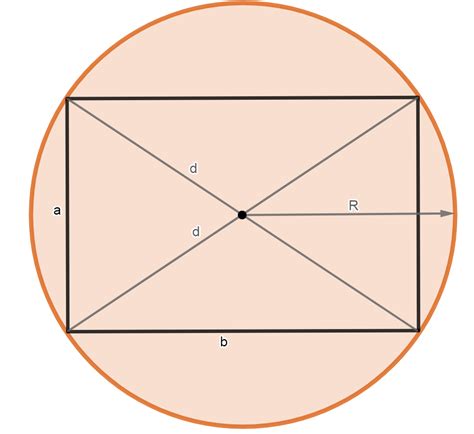
Теорема: Радиус описанной окружности прямоугольника равен половине длины его диагонали.
Доказательство: Рассмотрим прямоугольник ABCD, где AB и CD - его стороны, а AC и BD - его диагонали.
По определению описанной окружности, каждая сторона прямоугольника равна диаметру этой окружности. Таким образом, AB = CD = 2R, где R - радиус описанной окружности.
Диагональ AC является диаметром этой окружности, поэтому AC = 2R. Аналогично, BD = 2R.
По теореме о прямоугольнике, диагонали прямоугольника равны и пересекаются в его центре O. Таким образом, AC = BD и O является центром описанной окружности.
Поэтому R = AC/2 = BD/2 = AB/2. Таким образом, радиус описанной окружности равен половине длины диагонали прямоугольника.
Теорема доказана.
Формула для расчета радиуса описанной окружности прямоугольника
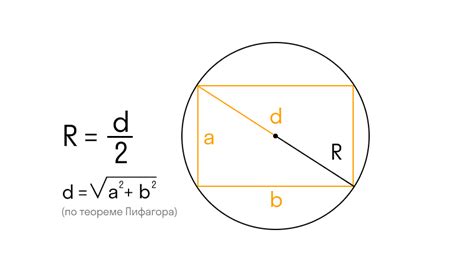
Для расчета радиуса описанной окружности прямоугольника необходимо знать длину его сторон. Пусть a и b - стороны прямоугольника. Тогда радиус описанной окружности можно найти по формуле:
Радиус = √((a/2)^2 + (b/2)^2)
В этой формуле a/2 и b/2 - половины сторон прямоугольника.
Зная значения сторон прямоугольника, можно при помощи данной формулы рассчитать радиус описанной окружности без особых трудностей.
Радиус описанной окружности является важным параметром для решения различных задач в геометрии и строительстве. Он позволяет определить центр окружности и провести соответствующие конструктивные работы.
Важно помнить, что прямоугольник должен быть вписан в окружность для корректного применения данной формулы.
Примеры вычисления радиуса описанной окружности
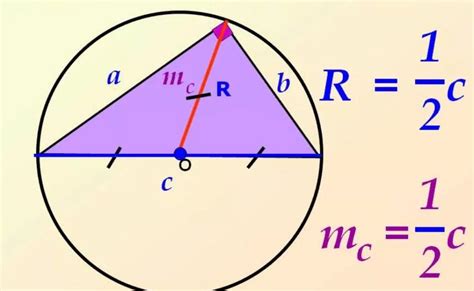
Чтобы вычислить радиус описанной окружности прямоугольника, нужно знать либо его длину и ширину, либо длины его диагоналей. Вот несколько примеров вычисления радиуса описанной окружности:
| Пример | Известные параметры | Радиус описанной окружности |
|---|---|---|
| Прямоугольник ABCD | Длина AB = 6 см Ширина BC = 4 см | r = √((AB/2)^2 + (BC/2)^2) |
| Прямоугольник PQRS | Диагональ PR = 10 см Диагональ QS = 8 см | r = √((PR/2)^2 + (QS/2)^2) |
В первом примере, чтобы найти радиус описанной окружности, мы используем половину длины AB и половину ширины BC в формуле квадрата суммы этих значений. Во втором примере, используем половину длины диагонали PR и половину длины диагонали QS.
Если известны только ширина и высота прямоугольника, вычисление радиуса может быть не таким простым. В этом случае, вам может понадобиться преобразование размеров или дополнительные операции для получения необходимой информации. Но для прямоугольников со сторонами, заданными длиной и шириной, представленными выше, все эти параметры легко вычисляются.
Упражнения для закрепления знаний о радиусе описанной окружности
- Возьмите лист бумаги и нарисуйте произвольный прямоугольник. С помощью школьного циркуля или линейки отметьте центр прямоугольника.
- Используя формулу радиуса описанной окружности для прямоугольников, вычислите радиус вашего прямоугольника и запишите его.
- Постройте описанную окружность вокруг вашего прямоугольника, используя полученный радиус. Для этого возьмите циркуль и проведите окружность, центр которой находится в центре прямоугольника.
- Проверьте правильность своих вычислений, измерив радиус описанной окружности с помощью линейки или мерного инструмента.
Выполнение данных упражнений поможет закрепить ваше понимание радиуса описанной окружности и его зависимость от основных параметров прямоугольника. Ответы на вопросы и результаты измерений можно записать в тетради или создать таблицу для последующего анализа.
Практическое применение радиуса описанной окружности прямоугольника
Радиус описанной окружности прямоугольника имеет важное значение во многих практических ситуациях. Он позволяет нам определить характеристики и свойства самого прямоугольника, а также использоваться в различных вычислениях и задачах.
1. Определение геометрических параметров
Радиус описанной окружности прямоугольника часто используется для определения других геометрических параметров этой фигуры. Например, зная значение радиуса описанной окружности и длины сторон прямоугольника, мы можем вычислить его площадь, периметр и диагонали. Эти данные особенно полезны в строительстве, архитектуре и дизайне, где необходимо точно определить размеры прямоугольной формы.
2. Построение циркулем и линейкой
Радиус описанной окружности прямоугольника позволяет нам построить эту фигуру с помощью циркуля и линейки. Для этого мы ставим кончик циркуля в центр окружности и рисуем круговую дугу с радиусом, равным радиусу описанной окружности. Затем мы соединяем точки пересечения дуги и сторон прямоугольника, и получаем точный рисунок прямоугольника.
3. Улучшение точности измерений
Использование радиуса описанной окружности прямоугольника позволяет повысить точность измерений других фигур или объектов. Например, мы можем улучшить точность измерений углов, длин и площадей, используя этот радиус совместно с другими геометрическими инструментами и формулами. Это особенно важно в научных и технических областях, где требуется высокая точность и надежность измерений.



