Радиус кривизны траектории протона – это величина, которая характеризует криволинейность пути движения протона при его движении в магнитном поле. Важно отметить, что протон – это положительно заряженная элементарная частица, которая обладает массой, а следовательно, при движении в магнитном поле она будет подвергаться силе Лоренца, изменяющей ее направление движения.
Радиус кривизны определяется следующей формулой: R = (m*v) / (q*B), где R – радиус кривизны траектории, m – масса протона, v – скорость протона, q – абсолютное значение заряда протона, B – индукция магнитного поля.
Из этой формулы видно, что радиус кривизны траектории протона при движении определяется массой, скоростью протона и индукцией магнитного поля. Чем больше скорость протона и магнитного поля, тем больше радиус кривизны. Это объясняется тем, что сила Лоренца, действующая на протон, пропорциональна скорости протона и индукции магнитного поля.
Чему равен радиус кривизны траектории протона?
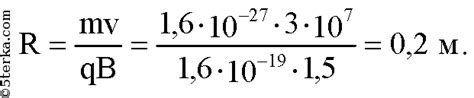
Радиус кривизны траектории протона при его движении зависит от магнитного поля, в котором он находится, и от его кинетической энергии. Определение радиуса кривизны траектории протона основано на изучении силы Лоренца, которую частичка испытывает под действием магнитного поля.
Из уравнения движения протона в магнитном поле получается следующая формула для радиуса кривизны:
r = p/(eB),
где r - радиус кривизны, p - импульс протона, e - заряд элементарной частицы (элементарный заряд), B - индукция магнитного поля.
Таким образом, радиус кривизны траектории протона обратно пропорционален индукции магнитного поля и импульсу протона. Чем сильнее магнитное поле и больше импульс протона, тем меньше радиус кривизны его траектории.
Знание радиуса кривизны траектории протона имеет большое значение для многих областей физики, включая ядерную физику, астрофизику и экспериментальную физику элементарных частиц. Изучение движения протона в магнитных полях позволяет улучшить точность измерения его параметров и получить новые данные о свойствах фундаментальных частиц.
Принципы движения протона в кривых пучках
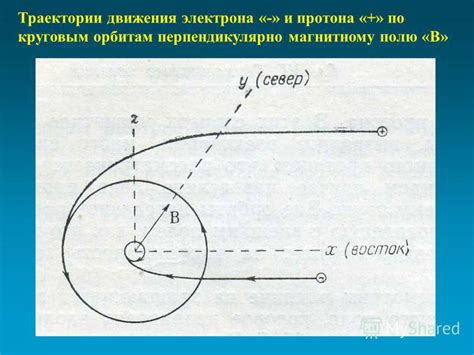
При движении протона в кривых пучках его траектория изгибается под воздействием магнитных полей, что позволяет удерживать его в замкнутом пучке. Радиус кривизны траектории протона определяется силой и направлением магнитного поля, а также его энергией и массой.
Чем сильнее магнитное поле и выше энергия протона, тем больше радиус кривизны его траектории. Это связано с тем, что сила, с которой магнитное поле действует на заряженную частицу, прямо пропорциональна силе и обратно пропорциональна радиусу кривизны.
Именно поэтому протоны с низкой энергией имеют более крупные радиусы кривизны траектории, чем протоны с высокой энергией. Это также объясняет, почему радиус кривизны траектории протона в кривых пучках может быть много больше радиуса пучка.
Важно отметить, что радиус кривизны траектории протона может меняться в зависимости от изменения магнитного поля, энергии или массы протона. Это можно использовать в управлении движением протона в кривых пучках, например, для фокусировки или разделения пучков.
Таким образом, принципы движения протона в кривых пучках определяются силой магнитного поля, энергией и массой протона, а также радиусом кривизны его траектории. Понимание этих принципов позволяет эффективно создавать и управлять кривыми пучками протонов в различных приложениях.
Уравнение радиуса кривизны траектории протона
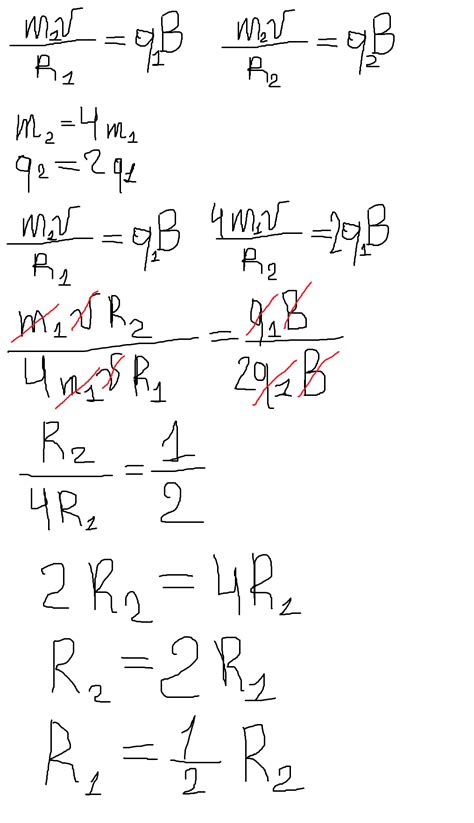
Уравнение радиуса кривизны траектории протона выглядит следующим образом:
r = m * v / (q * B)
где:
- r - радиус кривизны траектории;
- m - масса протона;
- v - скорость протона;
- q - заряд протона;
- B - индукция магнитного поля.
Таким образом, радиус кривизны траектории протона напрямую зависит от его массы, скорости и индукции магнитного поля.
Влияние сил на радиус кривизны траектории протона
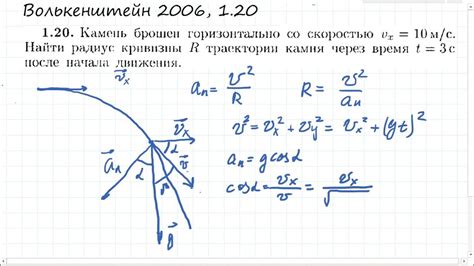
При движении протонов в магнитном поле или в электрическом поле на них действуют силы, которые влияют на радиус кривизны их траектории. Радиус кривизны траектории определяет изгиб траектории и зависит от величины и направления сил, действующих на протон.
В случае движения протона в магнитном поле, на него действует магнитная сила Лоренца. Эта сила перпендикулярна вектору скорости протона и вектору магнитного поля. Магнитная сила Лоренца оказывает центростремительное воздействие на протон, и его траектория становится кривой. Радиус кривизны траектории протона в магнитном поле определяется силой Лоренца и массой протона. Чем меньше радиус кривизны, тем сильнее и больше действующая на протон сила магнитного поля.
При движении протона в электрическом поле, на него действует электрическая сила. Если электрическое поле однородное, то радиус кривизны траектории протона определяется силой электрического поля и массой протона. Чем сильнее электрическое поле, тем меньше радиус кривизны траектории.
В общем случае, на протон могут одновременно действовать и магнитные и электрические силы. В таком случае радиус кривизны траектории протона будет определяться компромиссом между силами этих полей.
Для определения радиуса кривизны траектории протона можно воспользоваться формулой радиуса кривизны:
| Сила | Формула радиуса кривизны |
|---|---|
| Магнитная сила Лоренца | $$R = \frac{mv}{qB}$$ |
| Электрическая сила | $$R = \frac{mv}{qE}$$ |
Где:
- $$R$$ - радиус кривизны траектории протона
- $$m$$ - масса протона
- $$v$$ - скорость протона
- $$q$$ - заряд протона
- $$B$$ - магнитная индукция (в случае магнитного поля)
- $$E$$ - напряженность электрического поля (в случае электрического поля)
Таким образом, радиус кривизны траектории протона при движении зависит от сил, действующих на него, и является важным параметром при изучении движения частиц в электромагнитных полях.
Радиус кривизны траектории протона в электромагнитных полях

Радиус кривизны траектории протона при движении в электромагнитных полях определяется силой Лоренца, действующей на заряженную частицу.
Сила Лоренца представляет собой векторное произведение скорости протона и магнитной индукции поля:
F = q(v x B)
где F - сила Лоренца, q - заряд протона, v - его скорость, B - магнитная индукция поля.
Если протон движется со скоростью, перпендикулярной направлению магнитного поля, то сила Лоренца будет направлена центростремительно, и протон начнет движение по окружности.
Радиус кривизны траектории, на которой движется протон, определяется по формуле:
R = mv/qB
где R - радиус кривизны, m - масса протона, v - его скорость, q - заряд протона, B - магнитная индукция поля.
Таким образом, радиус кривизны траектории протона в электромагнитных полях зависит от его скорости, заряда и массы, а также от магнитной индукции поля.
Как изменяется радиус кривизны траектории протона при изменении массы?
Радиус кривизны траектории протона при движении зависит от его массы. Протон, как заряженная частица, двигается в магнитном поле силы Берзереля, где радиус кривизны траектории определяется взаимодействием между магнитным полем и самим протоном.
При изменении массы протона, его инерция также будет меняться. Изменение инерции приводит к изменению радиуса кривизны траектории протона. Согласно закону движения лоренце, радиус кривизны траектории обратно пропорционален квадрату массы протона.
Таким образом, при увеличении массы протона, радиус кривизны траектории будет увеличиваться, а при уменьшении массы протона, радиус кривизны траектории будет уменьшаться. Это связано с тем, что протон с большей массой требует большей силы для изменения его направления движения и, следовательно, имеет больший радиус кривизны траектории.
Применение радиуса кривизны траектории протона в физических экспериментах
Одним из основных применений радиуса кривизны траектории протона является измерение магнитного поля. Используя соотношение между радиусом кривизны, массой и зарядом протона, можно определить величину магнитного поля, воздействующего на заряженную частицу. Для этого необходимо измерить радиус кривизны и зная данные о массе протона и его заряде, рассчитать величину магнитного поля.
Также радиус кривизны траектории протона используется для определения заряда протона. Используя известные значения массы и радиуса кривизны, можно выразить заряд протона через эти величины. Этот метод позволяет определить заряд протона с высокой точностью и является важным для фундаментальных исследований в области физики элементарных частиц.
Таким образом, радиус кривизны траектории протона имеет важное значение в физических экспериментах, где изучается взаимодействие заряженных частиц в электромагнитном поле. Он используется для измерения магнитного поля и определения заряда протона, играя ключевую роль в определении основных свойств протона и его поведения в физических системах.



