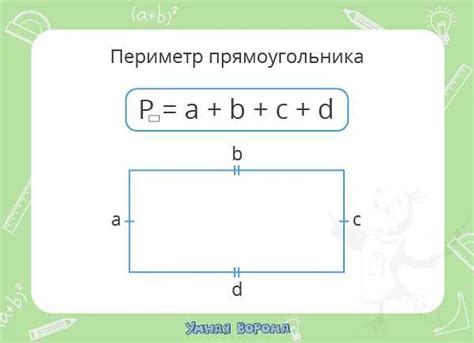
Периметр прямоугольника – это сумма длин всех его сторон. Для нахождения периметра есть несложная формула, которая может быть использована для любого прямоугольника:
Периметр = 2 * (Длина + Ширина)
Для понимания сути формулы, рассмотрим пример. Пусть у нас есть прямоугольник, длина которого равна 5 единицам, а ширина – 3 единицам. С помощью формулы находим периметр:
Периметр = 2 * (5 + 3) = 2 * 8 = 16 единиц
Таким образом, периметр этого прямоугольника равен 16 единицам. Формула может быть использована для любых прямоугольников, независимо от их размеров и пропорций.
Формула для расчета периметра прямоугольника

Периметр = 2 * (длина + ширина)
Где:
- Длина – это длина прямых сторон прямоугольника;
- Ширина – это длина прямых сторон, перпендикулярных к длине.
На практике, чтобы найти периметр прямоугольника, можно просто сложить все стороны прямоугольника и удвоить эту сумму.
Например, если длина прямоугольника равна 5 см, а ширина – 3 см, то периметр будет равен:
Периметр = 2 * (5 + 3) = 16 см.
Итак, формула для расчета периметра прямоугольника позволяет найти сумму всех его сторон и использовать эту величину в различных расчетах и задачах.
Примеры расчета периметра прямоугольника
Расчитаем периметр прямоугольника с длиной сторон 5 и 8:
Периметр = 2 * (длина + ширина) = 2 * (5 + 8) = 26.
Таким образом, периметр прямоугольника со сторонами 5 и 8 равен 26.
Давайте рассмотрим еще один пример: прямоугольник с длиной стороны 3 и шириной 6.
Периметр = 2 * (длина + ширина) = 2 * (3 + 6) = 18.
Значит, периметр прямоугольника со сторонами 3 и 6 равен 18.
Если стороны прямоугольника заданы переменными, то можно использовать их значения для расчета периметра. Например, если длина равна a и ширина равна b:
Периметр = 2 * (a + b).
С помощью этой формулы можно легко рассчитать периметр прямоугольника, зная значения его сторон.
Свойства периметра прямоугольника

1. Связь сторон с периметром. Периметр прямоугольника зависит от длин его сторон. Для прямоугольника с шириной а и высотой b периметр равен 2а + 2b. Эта формула говорит о том, что периметр состоит из двух кратных длин сторон прямоугольника.
2. Связь периметра с площадью. Площадь прямоугольника и его периметр тесно связаны между собой. Для прямоугольника с площадью S и периметром P справедлива формула: S = \(\frac{P}{2}\) · h, где h - высота прямоугольника.
3. Равенство диагоналей. В прямоугольнике диагонали равны между собой и делят его на два равных треугольника. Длина каждой диагонали равна \(\sqrt{a^2 + b^2}\), где a - ширина прямоугольника, а b - его высота.
Изучение свойств периметра прямоугольника поможет понять его характеристики и использовать их в практических задачах. Знание этих свойств позволяет легче расчитывать периметр и использовать его для нахождения других параметров фигуры.
Зависимость периметра прямоугольника от длин сторон

Зная длины сторон прямоугольника, можно легко вычислить его периметр. Например, если стороны прямоугольника равны 5 и 10, то периметр будет равен: P = 2*(5+10) = 30.
| Длина стороны a | Длина стороны b | Периметр прямоугольника P |
|---|---|---|
| 3 | 4 | 14 |
| 7 | 9 | 32 |
| 12 | 6 | 36 |
Как видно из таблицы, при изменении длин сторон прямоугольника, его периметр также изменяется. Если увеличить одну из сторон, периметр увеличится, а если уменьшить – периметр уменьшится. Это ясно и из формулы для вычисления периметра: P = 2*(a+b). Если сторона a увеличивается или уменьшается, то периметр тоже меняется, аналогично для стороны b.




