Точка пересечения высот представляет собой точку, в которой пересекаются все три высоты треугольника. Высота – это отрезок, соединяющий вершину треугольника с противоположной стороной и перпендикулярный данной стороне.
Высоты имеют важное смысловое значение в геометрии и играют важную роль в изучении треугольников. И именно в точке их пересечения они проявляют свои уникальные свойства. Одно из интересных свойств точки пересечения высот заключается в том, что она делит каждую высоту в отношении 2:1. То есть, если мы отложим от точки пересечения высот отрезки до вершин треугольника по высотам, то эти отрезки будут обладать следующим соотношением: длина сегмента от точки пересечения высот до вершины будет в два раза больше, чем длина сегмента от вершины до основания треугольника.
Точка пересечения высот - особая точка треугольника
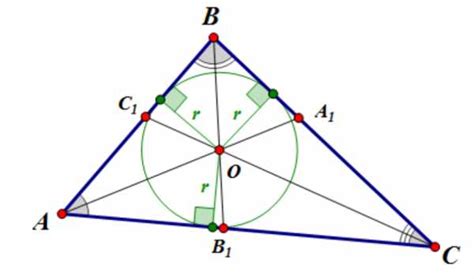
Существует несколько интересных фактов и свойств, связанных с точкой пересечения высот:
| 1. | Точка пересечения высот называется ортоцентром треугольника. |
| 2. | Ортоцентр лежит внутри, на сторонах или на продолжениях сторон треугольника в зависимости от его типа: остроугольный, тупоугольный или прямоугольный. |
| 3. | Длины отрезков, соединяющих вершины треугольника с ортоцентром, называются высотами треугольника. |
| 4. | Ортоцентр является точкой пересечения высот для всех треугольников, независимо от их размеров и формы. |
| 5. | Ортоцентр треугольника может совпадать с одной из его вершин только в особых случаях, например, в случае равнобедренного или равностороннего треугольника. |
Точка пересечения высот является важной геометрической характеристикой треугольника. Она играет значительную роль при решении различных задач и обладает множеством интересных свойств, изучение которых позволяет лучше понять структуру и геометрические связи в треугольнике.
Определение и свойства точки пересечения высот
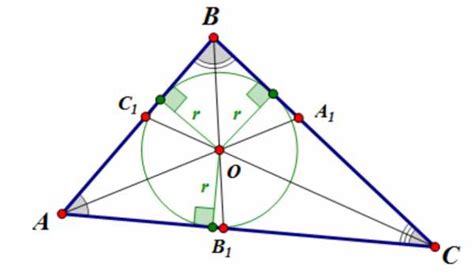
Точкой пересечения высот в треугольнике называется точка, где все высоты треугольника пересекаются. Другими словами, это точка, через которую можно провести прямые, соединяющие вершины треугольника с серединами противолежащих сторон.
Одно из главных свойств точки пересечения высот заключается в том, что она является ортоцентром треугольника. Ортоцентр – это точка пересечения высот, которая делит стороны треугольника в отношении 2:1 от вершины.
Еще одно интересное свойство точки пересечения высот заключается в том, что она лежит внутри треугольника, если треугольник – остроугольный, и снаружи, если треугольник – тупоугольный или прямоугольный. Это обусловлено тем, что ортоцентр является пересечением высот, которые в остроугольном треугольнике лежат внутри углов, а в тупоугольном или прямоугольном – за их пределами.
Точка пересечения высот имеет также одно важное свойство, связанное с ее отношением к центроиду и центру описанной окружности треугольника. Ортоцентр является антипараллельным центроиду и лежит на прямой, соединяющей центр описанной окружности и середину стороны треугольника. Это свойство играет важную роль при решении геометрических задач, связанных с треугольниками.
Как найти точку пересечения высот

Для нахождения точки пересечения высот в треугольнике необходимо выполнить следующие шаги:
- Проведите любую высоту треугольника из одной из его вершин. В результате получится отрезок, который соединяет вершину треугольника с противоположной стороной.
- Повторите шаг 1 для каждой из оставшихся вершин треугольника. В итоге получится еще два отрезка, соединяющих вершины треугольника с их противоположными сторонами.
- Найдите точку пересечения этих трех отрезков. Это и будет точка пересечения высот треугольника, или ортоцентр.
Заметим, что точка пересечения высот всегда находится внутри треугольника, независимо от его вида - остроугольный, тупоугольный или прямоугольный. Кроме того, она является важным геометрическим центром треугольника, так как из нее можно провести три перпендикуляра к сторонам треугольника.
Знание о местонахождении и свойствах точки пересечения высот позволит провести ряд интересных геометрических построений и решить множество задач, связанных с треугольниками.
Зависимость между сторонами треугольника и положением точки пересечения высот

Интересное свойство точки пересечения высот заключается в ее зависимости от сторон треугольника. Во-первых, ортоцентр всегда лежит внутри треугольника, если треугольник является остроугольным. Если треугольник прямоугольный, то ортоцентр совпадает с вершиной прямого угла.
Еще одно интересное свойство заключается в том, что если стороны треугольника равны или пропорциональны, то точка пересечения высот лежит на одной из сторон или их продолжении. В случае, когда треугольник является равносторонним, ортоцентр совпадает с центром масс треугольника.
Знание зависимости между сторонами треугольника и положением точки пересечения высот позволяет более глубоко изучить его свойства и использовать их в решении геометрических задач.
Треугольники со специальными свойствами точки пересечения высот
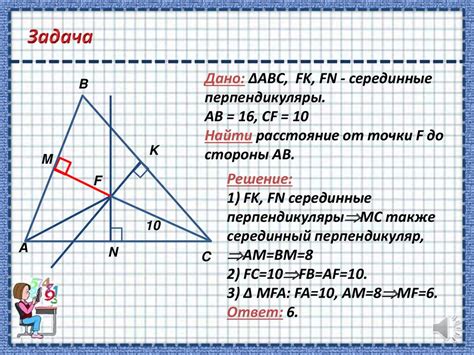
Одно из основных свойств точки пересечения высот заключается в том, что она является центром описанной окружности треугольника. Это значит, что если провести окружность, проходящую через вершины треугольника и имеющую точку пересечения высот в качестве центра, то она будет проходить также через середины сторон треугольника.
Другое интересное свойство точки пересечения высот состоит в том, что она делит высоты треугольника в отношении 2:1. То есть, если обозначить точку пересечения высот буквой H, то отрезки HA, HB и HC, где A, B и C – вершины треугольника, будут иметь следующие соотношения: HA:HB:HC = 2:1.
Эта особая точка также называется ортоцентром треугольника. Ортоцентр может лежать внутри, на сторонах или даже вне треугольника, в зависимости от его формы и угловых размеров. Например, в остроугольном треугольнике ортоцентр всегда будет лежать внутри фигуры, в тупоугольном треугольнике – на продолжении одной его стороны, а в прямоугольном треугольнике – на вершине с прямым углом.
Треугольники со специальными свойствами точки пересечения высот представляют особый интерес в геометрии и математике. Изучение этих свойств позволяет получить дополнительные знания о треугольниках и расширить представление о структуре геометрических фигур. Точка пересечения высот – это не просто одна из множества точек в треугольнике, она является основой для изучения и понимания многих закономерностей и зависимостей, связанных с данной фигурой.
Прикладные задачи, связанные с точкой пересечения высот в треугольнике
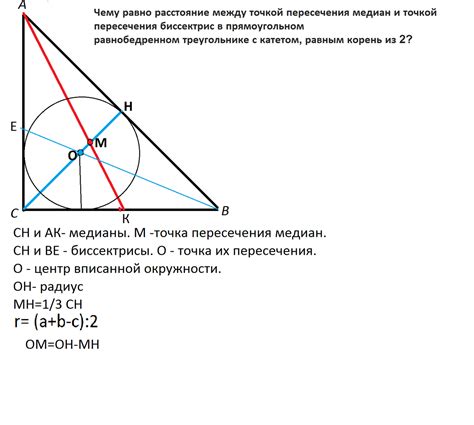
1. Нахождение центра описанной окружности
Точка пересечения высот является центром описанной окружности треугольника. Описанная окружность - это окружность, которая проходит через все вершины треугольника. Это свойство точки пересечения высот позволяет использовать ее для определения радиуса и координат центра описанной окружности. Это может быть полезно при решении задач, связанных с геометрией или треугольными фигурами.
2. Нахождение площади треугольника
Точка пересечения высот также позволяет легко найти площадь треугольника. Положение точки пересечения высот внутри треугольника гарантирует, что все три отрезка, соединяющие вершины треугольника с точкой пересечения, являются высотами. Площадь треугольника можно найти, используя формулу: площадь = 0,5 * основание * высота.
3. Нахождение центра тяжести треугольника
Центр тяжести треугольника - это точка, в которой сумма координат всех вершин треугольника делится на три. Точка пересечения высот является центром тяжести треугольника. Это свойство позволяет использовать точку пересечения высот для определения координат центра тяжести и решения задач, связанных с равновесием или распределением массы.
Точка пересечения высот в треугольнике имеет множество других прикладных применений и свойств, которые могут быть использованы в различных задачах. Изучение и понимание этих свойств помогает лучше понять геометрию треугольников и их взаимосвязь с другими геометрическими фигурами и понятиями.
Интересные факты о точке пересечения высот

1. Называется она ортоцентром.
Точка пересечения высот в треугольнике выполняет роль особого и важного элемента. Она называется ортоцентром треугольника. Термин "ортоцентр" происходит от греческого слова "ορθος", что означает "перпендикуляр". Ортоцентр - это точка, которая лежит на пересечении высот, ведущих из каждого из вершин треугольника.
2. Не всегда находится внутри треугольника.
Ортоцентр может находиться внутри треугольника, на его сторонах или даже вне его. Существует несколько случаев расположения ортоцентра:
- Внутри треугольника: в этом случае треугольник называется остроугольным.
- На сторонах треугольника: в этом случае треугольник называется прямоугольным.
- Вне треугольника: в этом случае треугольник называется тупоугольным.
3. Является центром описанной окружности.
Ортоцентр также является центром описанной окружности треугольника, то есть окружности, проходящей через все вершины треугольника. Каждая сторона треугольника является хордой этой окружности.
4. Совпадает с центром симедиан.
Ортоцентр также совпадает с центром симедиан, которая является линией, соединяющей каждую вершину треугольника с точкой, делящей соответствующую сторону треугольника пополам. Симедиана также делит другие медианы и другие линии, проходящие через центр, пополам.
5. Симметричен относительно серединных перпендикуляров.
Если нарисовать серединные перпендикуляры к каждой стороне треугольника, они все пересекутся в ортоцентре. Ортоцентр также является симметричным относительно серединных перпендикуляров, что означает, что расстояние от середины каждой стороны до ортоцентра равно.
Значение точки пересечения высот для практики строительства и геометрии
В строительстве точка пересечения высот играет ключевую роль при построении фундамента зданий и сооружений. Она помогает определить оптимальное местоположение для установки опорных столбов или пилонов, обеспечивающих стабильность и прочность конструкции. Зная положение ортоцентра, инженеры могут рассчитать необходимые параметры и распределение нагрузок на фундамент, что позволяет предотвратить возможные повреждения или ослабления конструкции в будущем.
Ортоцентр также используется в дизайне интерьера и архитектуре. Его положение в треугольной комнате может помочь решить проблему размещения мебели и создания гармоничного пространства. Зная точку пересечения высот, дизайнеры могут определить оптимальное расположение кресел, столов, шкафов и других предметов интерьера, что поможет создать функциональное и эстетически привлекательное помещение.
В области геометрического анализа точка пересечения высот является важным инструментом для изучения свойств треугольников. Она помогает определить различные параметры треугольников, такие как площадь, центр масс, радиусы вписанной и описанной окружностей. Зная координаты ортоцентра, можно выявить особенности треугольника, его симметрию и взаимосвязь между его сторонами и углами.
Таким образом, значение точки пересечения высот в треугольнике не ограничивается только областью геометрии, она имеет практическое применение в строительстве, дизайне и геометрическом анализе. Благодаря уникальным свойствам ортоцентра, его положение может оказать существенное влияние на конструкцию и организацию пространства, делая его незаменимым инструментом для многих задач и проектов.



