В математике и анализе функций существуют различные типы точек, которые могут быть интересны при изучении их свойств и поведения. Два таких типа точек - это точки экстремума и критические точки. Хотя эти термины могут показаться похожими, они имеют свои уникальные характеристики и связи с производной функции.
Точка экстремума - это точка, где значение функции достигает локального максимума или минимума. Представьте себе функцию, которая моделирует изменение чего-либо в зависимости от времени. В точке экстремума происходит изменение тренда - от роста к падению или наоборот. Такие точки можно найти, используя производную функции, которая показывает скорость изменения функции в каждой ее точке.
Критическая точка, с другой стороны, является точкой, где производная функции равна нулю или не существует. Другими словами, это место, где скорость изменения функции обращается в ноль или не определена. Критическая точка может быть точкой экстремума - то есть, местом, где функция достигает максимума или минимума, или она может быть точкой перегиба, где меняется выпуклость функции.
Важно отметить, что все точки экстремума являются критическими точками, но не все критические точки являются точками экстремума. Кроме того, в случае многомерных функций, критические точки называются стационарными точками, так как они являются местами, где градиент функции равен нулю.
Раздел 1: Определение точек экстремума
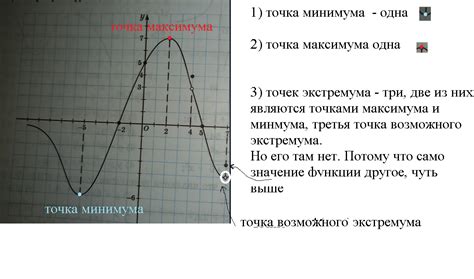
Если функция имеет точку экстремума, то её производная в этой точке равна нулю или не определена. Исследование функции на экстремум включает поиск таких точек и анализ их характера.
Существует два типа точек экстремума: локальный минимум и локальный максимум.
- Локальный минимум - это точка, в которой функция достигает наименьшего значения в заданной окрестности. Производная функции в такой точке изменяет знак с отрицательного на положительный.
- Локальный максимум - это точка, в которой функция достигает наибольшего значения в заданной окрестности. Производная функции в такой точке изменяет знак с положительного на отрицательный.
Точка экстремума может быть также глобальным минимумом или максимумом, если функция достигает наименьшего или наибольшего значения на всей области определения.
Определение точек экстремума важно для анализа поведения функций и использования их в различных задачах математики, физики, экономики и других наук.
Что такое точки экстремума
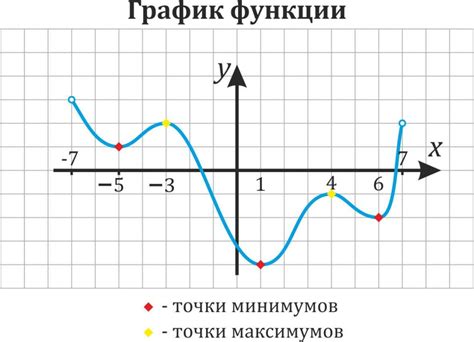
Точками экстремума называются те точки функции, в которых она достигает локального минимума или максимума. Это означает, что значение функции в точке экстремума будет самым маленьким или самым большим среди значений функции в некоторой окрестности этой точки.
Точка экстремума называется максимумом, если слева от этой точки производная функции положительна, а справа от неё – отрицательна. Аналогичным образом, точка экстремума называется минимумом, если слева от неё производная функции отрицательна, а справа – положительна.
Точками экстремума могут быть как внутренние точки функции, так и точки, являющиеся её граничными значениями. Кроме того, функция может не иметь точек экстремума.
Определение и изучение точек экстремума функции является важным инструментом в математическом анализе и науках, где требуется изучение поведения функций и определение их наиболее и наименее значимых значений.
Раздел 2: Определение критических точек

Для определения критических точек необходимо найти точки, где первая производная функции равна нулю или не существует. Если первая производная равна нулю, то это точка, где у функции может быть локальный максимум или минимум, либо точка перегиба. Однако, не все точки, где первая производная равна нулю, являются критическими. Некоторые из них могут не существовать или быть фиктивными. Поэтому, для определения критических точек необходимо провести дополнительные исследования функции.
Критические точки имеют важное значение при анализе функций, так как они могут помочь найти экстремумы функции и решить различные математические задачи. Понимание разницы между точками экстремума и критическими точками позволяет более точно анализировать функции и прогнозировать их поведение.
Что такое критические точки

Критические точки могут быть как максимумами, так и минимумами функции, а также точками перегиба. Для определения типа каждой критической точки необходимо проанализировать вторую производную функции и знаки в окрестности этой точки.
При анализе критических точек необходимо учитывать, что не каждая критическая точка является точкой экстремума. Некоторые критические точки могут быть точками перегиба, когда функция изменяет свою выпуклость или вогнутость.
Критические точки позволяют определить наиболее важные точки на графике функции и помогают в понимании ее поведения. Исследование критических точек полезно в различных областях, таких как оптимизация, физика, экономика и другие.
Раздел 3: Значение производной в точках экстремума

В предыдущем разделе мы рассмотрели, что такое точки экстремума и что такое критические точки. Теперь давайте разберемся, как определить значение производной в точках экстремума.
Точки экстремума являются местами, где производная функции равна нулю или не существует. Это означает, что в этих точках график функции меняет свое направление и достигает максимального или минимального значения.
Для определения значения производной в точках экстремума мы используем вторую производную. Если вторая производная положительна в точке экстремума, то это будет минимум, а если вторая производная отрицательна, то это будет максимум.
| Значение второй производной | Тип точки экстремума |
|---|---|
| Положительное | Минимум |
| Отрицательное | Максимум |
Таким образом, значение производной в точке экстремума позволяет определить ее тип (минимум или максимум). Это важное понятие в анализе функций и нахождении оптимальных значений в задачах оптимизации.
Связь производной с точками экстремума
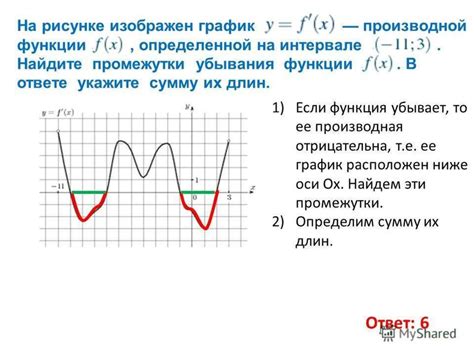
Существует тесная связь между производной функции и точками экстремума. В точке экстремума производная функции равна нулю или не существует. Это связано с тем, что в точке экстремума график функции меняет свой наклон с положительного на отрицательный или наоборот.
Для понимания связи производной с точками экстремума, рассмотрим пример. Пусть у нас есть функция f(x), производная которой обозначается f'(x). Если f'(x) равна нулю или не существует в точке x0, то x0 является одной из точек экстремума функции f(x).
Существует несколько типов точек экстремума, определение которых также связано с производной функции:
- Максимум – точка экстремума, в которой функция принимает наибольшее значение. В такой точке производная функции меняет знак с положительного на отрицательный.
- Минимум – точка экстремума, в которой функция принимает наименьшее значение. В такой точке производная функции меняет знак с отрицательного на положительный.
- Точка перегиба – точка, в которой меняется направление выпуклости функции. В такой точке производная функции равна нулю, но она не является точкой экстремума.
Использование производной функции позволяет определить точки экстремума, а также классифицировать их по типу. Это помогает понять поведение функции и найти её наибольшие или наименьшие значения.
Раздел 4: Значение производной в критических точках
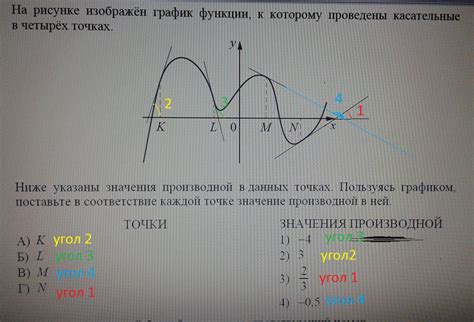
Значение производной в критической точке позволяет определить тип экстремума функции. Если значение производной меняется на противоположные знаки при переходе через критическую точку, то функция имеет локальный максимум или минимум в этой точке. Если значение производной не меняется на противоположные знаки при переходе через критическую точку, то функция не имеет экстремума в этой точке.
Однако, необходимо учитывать, что существуют и другие способы определения экстремумов функций, например, методы второй производной или графический анализ. Использование трех и более производных позволяет определить тип экстремума с точностью.
Таким образом, значение производной в критических точках является важным инструментом для определения экстремумов функций. Исследование производной в максимумах и минимумах функций позволяет понять их поведение и использовать их в математическом моделировании и решении задач различных областей науки и техники.
Связь производной с критическими точками
Если производная функции равна нулю в некоторой точке, то это может быть точкой экстремума функции. Однако не все точки, где производная равна нулю, являются точками экстремума. Некоторые из них могут быть точками перегиба, где функция меняет свой выпуклый или вогнутый характер.
Для определения характера точек, где производная равна нулю или не существует, можно использовать вторую производную. Если вторая производная больше нуля, то это указывает на локальный минимум функции в данной точке. Если же вторая производная меньше нуля, то это указывает на локальный максимум функции. Если же вторая производная равна нулю или не существует, то точка может быть либо точкой перегиба, либо исключительной точкой.
Критические точки являются ключевыми для определения экстремумов функций, так как именно в них функция может достигать минимальных или максимальных значений. Исследование их свойств и характеризация помогают понять поведение функции в окрестности данных точек.
| Тип точки | Условия на производные | Характер точки |
|---|---|---|
| Минимум | Производная = 0, Вторая производная > 0 | Локальный минимум |
| Максимум | Производная = 0, Вторая производная < 0 | Локальный максимум |
| Перегиб | Производная = 0, Вторая производная = 0 или не существует | Точка перегиба |
Исследование критических точек позволяет определить наличие и тип экстремумов функции. Таким образом, связь производной с критическими точками играет важную роль в изучении и анализе функций.
Раздел 5: Отличия точек экстремума от критических точек

В математическом анализе точки экстремума и критические точки имеют важные различия. В этом разделе мы рассмотрим эти различия и их применение в различных областях.
Точки экстремума функции являются ее локальными максимумами или минимумами. Локальный максимум - это точка, в которой функция достигает наибольшего значения в некоторой окрестности этой точки. Локальный минимум - это точка, в которой функция достигает наименьшего значения. Чтобы найти точки экстремума, можно продифференцировать функцию и найти ее критические точки.
Критическая точка функции - это точка, в которой производная функции равна нулю или не определена. Мы можем использовать критические точки для анализа поведения функции. Если критическая точка - это точка экстремума, то производная меняет знак на этой точке. Если же критическая точка не является точкой экстремума, то производная будет менять знак на близлежащих точках.
Основное различие между точками экстремума и критическими точками состоит в их определении. Точка экстремума - это точка, в которой функция достигает наибольшего или наименьшего значения, а критическая точка - это точка, в которой производная функции равна нулю или не определена.
Важно понимать, что не все критические точки являются точками экстремума, и не все точки экстремума являются критическими точками. Точки экстремума можно найти с помощью производных функции, в то время как критические точки могут быть найдены путем нахождения корней производной.
Различия между точками экстремума и критическими точками играют важную роль в анализе функций и их поведении. Правильное определение и использование этих понятий помогает в изучении оптимизации функций, определении глобальных экстремумов и нахождении значимых точек функций.
Сравнение точек экстремума и критических точек
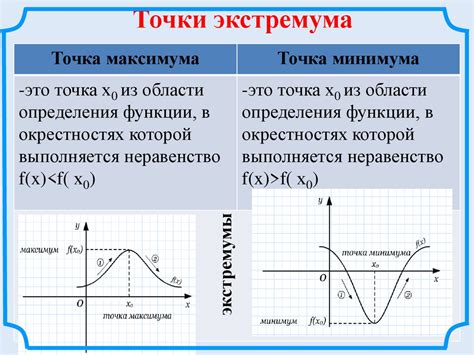
Вот основные различия между этими двумя видами точек:
| Точки экстремума | Критические точки |
|---|---|
| Точки, в которых функция достигает максимального или минимального значения | Точки, в которых производная функции равна нулю или не существует |
| Можно найти, решив уравнение производной функции | Можно найти, приравняв производную функции к нулю и решив уравнение |
| Существуют локальные и глобальные точки экстремума | Критические точки могут быть экстремальными или нет |
Однако, важно отметить, что не все точки экстремума являются критическими точками, и не все критические точки являются точками экстремума. Точка, где производная функции равна нулю или не существует, может быть «плоским пиком» или разрывом функции, а не точкой экстремума.
Поэтому, для более точного анализа функции, необходимо изучать не только точки экстремума, но и другие свойства функции, такие как выпуклость или вогнутость, наличие границ, и поведение на бесконечности.



