Учение о периметре и площади - одна из основ математики, которую изучают уже в начальной школе. Эти понятия играют важную роль в различных областях жизни и проявляются на практике в решении разнообразных задач.
Периметр - это длина границы фигуры. Он измеряется в единицах длины, таких как сантиметры или метры. Для простых фигур, например, квадрата или прямоугольника, периметр можно вычислить по формуле, сложив длины всех его сторон.
Площадь же представляет собой количество пространства, занимаемого фигурой. Она измеряется в квадратных единицах, таких как квадратные сантиметры или квадратные метры. Для простых фигур, площадь также можно вычислить по формулам, исходя из их формы и размеров.
Периметр и площадь – важные понятия для изучения геометрии в 3 классе
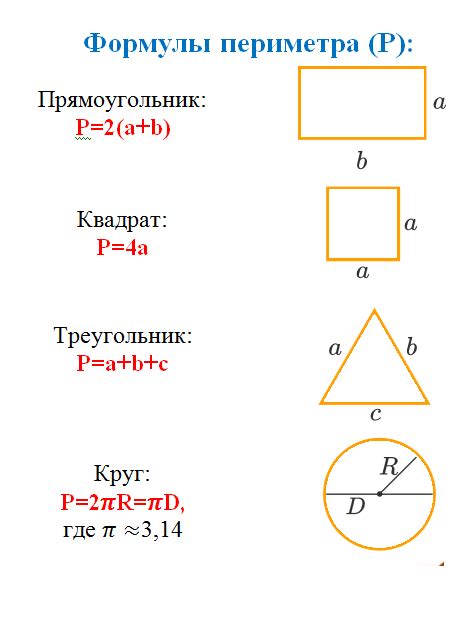
Периметр - это длина окружности, которая ограничивает какую-либо фигуру. Например, для прямоугольника периметр можно найти, сложив длины всех его сторон. Для треугольника - сложив длины всех его сторон. Зная периметр, можно определить, насколько длинной нитью нужно обернуть фигуру.
Площадь - это понятие, связанное с понятием площади основы. Так, площадь прямоугольника можно получить, перемножив длину и ширину. Площадь треугольника можно найти, умножив половину длины основания на высоту. Площадь показывает, сколько монет нужно для покрытия поверхности фигуры.
Умение находить периметр и площадь различных фигур - важные навыки, которые позволяют детям анализировать и измерять различные объекты вокруг себя. Эти понятия также лежат в основе более сложных геометрических задач, которые будут изучаться в старших классах.
Определение периметра и площади
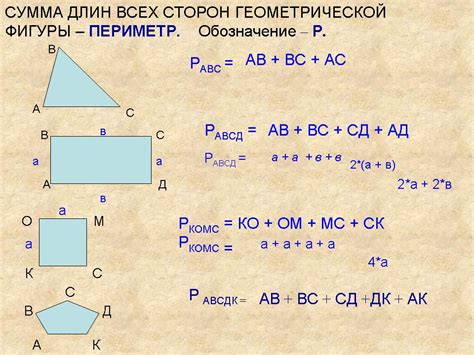
Периметр – это длина границы фигуры, то есть сумма всех ее сторон. Мы можем найти периметр не только для простых фигур, таких как квадраты или прямоугольники, но и для сложных форм, таких как многоугольники или окружности. Для каждой фигуры существует своя формула для нахождения периметра.
Площадь – это понятие, которое используется для измерения площади поверхности фигуры. Она обозначает, сколько плоской фигуры занимает пространства. У каждой фигуры, также есть своя формула для нахождения площади.
Знание периметра и площади помогает нам решать различные задачи в геометрии и применять их в реальной жизни. Например, знание периметра и площади прямоугольника помогает нам рассчитать сколько забора нужно для ограждения сада или рассчитать площадь комнаты для покупки коврового покрытия.
Таким образом, периметр и площадь являются фундаментальными понятиями в геометрии, которые помогают нам анализировать и измерять фигуры.
Отличия между периметром и площадью
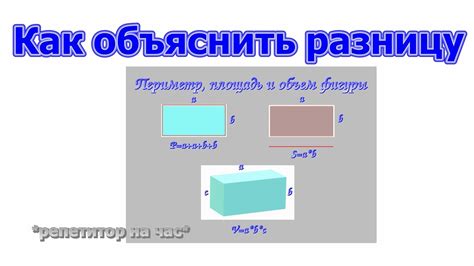
Периметр – это длина замкнутой линии, ограничивающей фигуру. Другими словами, периметр представляет собой сумму всех сторон фигуры. Например, если у нас есть прямоугольник с длиной сторон 5 и 3, то периметр будет равен 16 (5 + 3 + 5 + 3). Периметр измеряется в единицах длины, таких как сантиметры или метры.
Площадь – это мера поверхности, занимаемой фигурой. Она показывает, сколько площади занимает фигура на плоскости. Например, если у нас есть прямоугольник с длиной сторон 5 и 3, то площадь будет равна 15 (5 * 3). Площадь измеряется в квадратных единицах длины, таких как квадратные сантиметры или квадратные метры.
Таким образом, основное отличие между периметром и площадью заключается в том, что периметр измеряет длину линии, ограничивающей фигуру, а площадь измеряет поверхность, занимаемую фигурой. Периметр используется для измерения длины забора вокруг сада, а площадь помогает определить, сколько плиток понадобится для покрытия пола.
Как вычислить периметр треугольника и квадрата
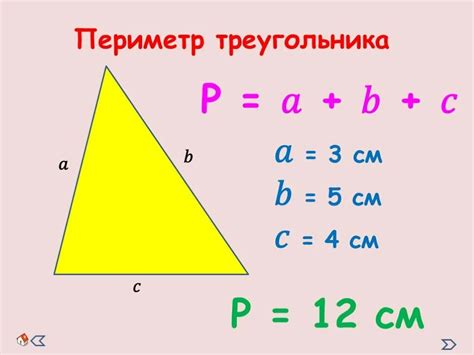
Периметр треугольника = Сторона 1 + Сторона 2 + Сторона 3
Например, если длины сторон треугольника равны 5 см, 7 см и 9 см, то периметр треугольника будет равен 5 см + 7 см + 9 см = 21 см.
У квадрата все стороны равны между собой, поэтому периметр квадрата можно найти, умножив длину одной стороны на 4:
Периметр квадрата = Сторона × 4
Например, если длина стороны квадрата равна 6 см, то периметр квадрата будет равен 6 см × 4 = 24 см.
Таким образом, чтобы вычислить периметр треугольника или квадрата, нужно знать длины их сторон и применить соответствующую формулу.
Как вычислить площадь прямоугольника и квадрата
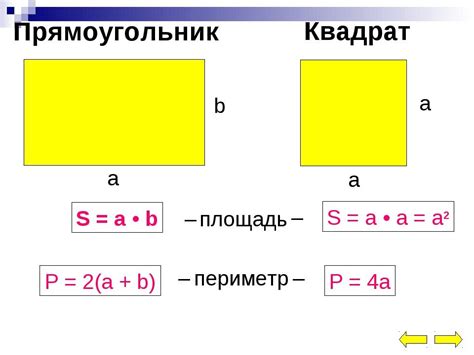
Чтобы вычислить площадь прямоугольника, необходимо знать длину одной из его сторон (сторона a) и длину другой стороны (сторона b). Площадь S прямоугольника можно найти по формуле S = a * b. Например, если сторона a равна 5 см, а сторона b равна 7 см, то площадь прямоугольника будет равна 5 * 7 = 35 см².
Квадрат - это частный случай прямоугольника, у которого все стороны равны между собой. Площадь квадрата можно найти по формуле S = a², где a - длина стороны квадрата. Например, если сторона квадрата равна 4 см, то площадь квадрата будет равна 4² = 16 см².
| Фигура | Формула площади |
|---|---|
| Прямоугольник | S = a * b |
| Квадрат | S = a² |
Теперь, зная формулы для вычисления площади прямоугольника и квадрата, вы можете легко решать задачи, связанные с этими фигурами.
Практическое применение знаний о периметре и площади в повседневной жизни

Умение работать с периметром и площадью имеет практическое применение во многих аспектах нашей повседневной жизни. Знание этих понятий и умение их применять позволяют нам разобраться с различными задачами, связанными с измерениями и планированием.
Периметр – это длина замкнутой кривой, которая ограничивает геометрическую фигуру. Знание периметра может быть полезно, например, при планировании ограды вокруг участка. Рассчитав периметр участка, мы сможем точно оценить количество материала, необходимого для постройки ограды и предварительно рассчитать стоимость проекта.
Площадь – это мера поверхности фигуры, занимаемой этой фигурой в плоскости. Знание площади может быть полезно при покупке ковра или плитки для укладки пола. Рассчитав площадь помещения, мы сможем определить необходимое количество материала, чтобы выполнить работу без лишнего расхода средств.
Знание периметра и площади также полезно при работе с картами и планами. Например, если мы понимаем, что масштаб карты 1 см на плане равен 1 км в реальности, то мы сможем оценить расстояния между населенными пунктами или размеры территории.
Интересно, что умение рассчитать периметр и площадь может пригодиться не только в геометрии, но и в других науках и областях. Например, в архитектуре, инженерии, географии, экологии, агрономии, экономике и многих других дисциплинах. Понимание этих понятий помогает в решении различных вычислительных задач, позволяет делать предположения и прогнозы.
Таким образом, знание периметра и площади имеет практическое значение в повседневной жизни. Эти понятия помогают нам в планировании, строительстве, покупке и других сферах деятельности, где необходимо оценивать и измерять поверхности и расстояния. Поэтому, освоение этих понятий в раннем возрасте, в частности, в 3 классе, является важным шагом к развитию математической грамотности и практических навыков.



